天津市红桥区2019-2020学年九年级上学期数学期中试卷

试卷更新日期：2020-09-23 类型：期中考试

进入出卷网下载

一、单选题

1. 下列函数中是二次函数的是（　　）

A、y＝﹣2x B、y＝﹣ $\frac{6}{x}$ C、y＝1﹣3x² D、y＝x+3

查看试题解析
2. 下列图形中，可以看作是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 已知一元二次方程x²+kx-3=0有一个根为1，则k的值为（）

A、−2 B、2 C、−4 D、4

查看试题解析
4. 如图，AB为⊙O的直径，点C在⊙O上，若∠OCA＝55°，则∠BOC等于（　　）

A、105° B、110° C、115° D、125°

查看试题解析
5. 如图，⊙O是△ABC的外接圆，⊙O的半径为3，∠A=45°，则 $\overset{⌢}{B C}$ 的长是（）

A、 $\frac{3}{4} π$ B、 $\frac{3}{2} π$ C、 $\frac{45}{2} π$ D、 $\frac{9}{4} π$

查看试题解析
6. 已知正六边形的边长是2，则该正六边形的边心距是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $\frac{\sqrt{3}}{2}$

查看试题解析
7. 在Rt△ABC中，∠C=90°，AB=10．若以点C为圆心，CB为半径的圆恰好经过AB的中点D，则AC=（）

A、5 B、 $5 \sqrt{2}$ C、 $5 \sqrt{3}$ D、6

查看试题解析
8. 如图，AB为⊙O的直径，PD切⊙O于点C ，交AB的延长线于D ，且∠D＝40°，则∠PCA等于（　　）

A、50° B、60° C、65° D、75°

查看试题解析
9. 若点A（﹣3，y₁），B（﹣2，y₂），C（2，y₃）都在二次函数y＝x²+2x﹣1的图象上，则y₁ ， y₂ ， y₃的大小关系是（　　）

A、y₃＜y₁＜y₂ B、y₂＜y₁＜y₃ C、y₁＜y₂＜y₃ D、y₃＜y₂＜y₁

查看试题解析
10. 服装店将进价为每件100元的服装按每件x（x＞100）元出售，每天可销售（200﹣x）件，若想获得最大利润，则x应定为（　　）

A、150元 B、160元 C、170元 D、180元

查看试题解析
11. 如图，将 $Δ A B C$ 绕点C顺时针旋转得到 $Δ D E C$ ，使点A的对应点D恰好落在边 $A B$ 上，点B的对应点为E，连接 $B E$ ．下列结论一定正确的是（）

A、 $A C = A D$ B、 $A B ⊥ E B$ C、 $B C = D E$ D、 $∠ A = ∠ E B C$

查看试题解析
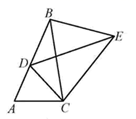12. 二次函数y＝ax²+bx（a ， b为常数）的图象如图所示，设关于x的一元二次方程ax²+bx+m＝1的两个实数根分别为x₁ ， x₂ ，若x₁•x₂＞0，则实数m的取值范围是（　　）

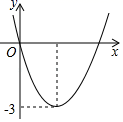A、0≤m＜3 B、0＜m≤3 C、1≤m＜4 D、1＜m≤4

查看试题解析

二、填空题

13. 二次函数y=x²﹣2x+3的最小值是．

查看试题解析
14. 若关于x的一元二次方程x²﹣4x+m＝0没有实数根，则m的取值范围是．

查看试题解析
15. 如图，PA，PB分别切⊙O于点A，B.若∠P＝100°，则∠ACB的大小为（度）.

查看试题解析
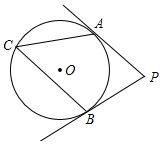16. 在平面直角坐标系中，若点A（x+1，2y+1）与点A'（y﹣2，x）关于原点O对称，则代数式x²﹣y²的值为．

查看试题解析
17. 如图，四边形ABCD内接于⊙O ， ∠B＝90°，AD＝3，CD＝2，则S_△_OCD的值为．

查看试题解析
18. Rt△ABC中，已知∠C＝90°，∠B＝50°，点D在边BC上，BD＝2CD（如图）．把△ABC绕着点D逆时针旋转m（0＜m＜180）度后，如果点B恰好落在初始Rt△ABC的边上，那么m＝．

查看试题解析

三、解答题

19. 解下列关于x的方程

(1)、（1）x²﹣6x﹣7＝0

(2)、2x²﹣x﹣2＝0

查看试题解析
20. 已知函数y＝﹣x^m^﹣¹+bx﹣3（m ， b为常数）是二次函数，其图象的对称轴为直线x＝1

(1)、求该二次函教的解析式；

(2)、当﹣2≤x≤0时，求该二次函数的函数值y的取值范围．

查看试题解析
21. 已知△ABC是⊙O的内接三角形，∠BAC的平分线交⊙O于点D ．

(1)、如图①，若BC是⊙O的直径，BC＝4，求BD的长；

(2)、如图②，若∠ABC的平分线交AD于点E ，求证：DE＝DB ．

查看试题解析
22. 已知AB是⊙O的直径，AT是⊙O的切线，∠ABT=50°，BT交⊙O于点C，E是AB上一点，延长CE交⊙O于点D．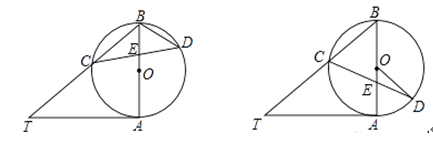

(1)、如图①，求∠T和∠CDB的大小；

(2)、如图②，当BE=BC，求∠CDO的大小.

查看试题解析
23. 如图，用一段长为30m的篱笆围成一个一边靠墙的矩形菜园，墙长为18m ．设矩形菜园的边AB的长为xm ，面积为Sm² ．

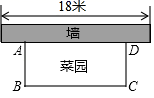(1)、写出S关于x的函数解析式，并求出x的取值范围；

(2)、当该矩形菜园的面积为72m²时，求边AB的长；

(3)、当边AB的长为多少时，该矩形菜园的面积最大？最大面积是多少？

查看试题解析
24. 在矩形ABCD中，AB＝2，∠ACB＝30°，将矩形ABCD绕点A逆时针方向旋转，得到矩形AB′C′D′，记旋转角为α（0＜α＜90°）．

(1)、如图①，当B'C'过点D时，求△ADC'的面积S的值；

(2)、如图②，当点B的对应点B'落在AC上时，在B′C′上取点E ，使B'E＝AB ．
①求∠EBB'的大小；

②求BE的长（直接写出结果即可）．

查看试题解析
25. 已知抛物线y＝﹣x²+bx+c经过点C（0，3），与x轴交于A ， B两点，点A（﹣1，0）．

(1)、求该抛物线的解析式；

(2)、D为抛物线对称轴上一点，当△ACD的周长最小时，求点D的坐标；

(3)、在抛物线上是否存在一点P ，使CP恰好将以A ， B ， C ， P为顶点的四边形的面积分为相等的两部分？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析