天津市和平区2019-2020学年九年级上学期数学期中试卷
试卷更新日期:2020-09-23 类型:期中考试
一、单选题
-
1. 下列图形中,可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知 的半径为 ,点P到圆心O的距离为 ,则点 和 的位置关系是( )A、点P在圆内 B、点P在圆上 C、点P在圆外 D、不能确定3. 用配方法解一元二次方程x2﹣4x+2=0,下列配方正确的是( )A、(x+2)2=2 B、(x﹣2)2=﹣2 C、(x﹣2)2=2 D、(x﹣2)2=64. 二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到,下列平移正确的是( )A、先向左平移2个单位,再先向上平移1个单位 B、先向左平移2个单位,再先向下平移1个单位 C、先向右平移2个单位,再先向上平移1个单位 D、先向右平移2个单位,再先向下平移1个单位5. 某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )A、 B、 C、 D、6. 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )
2. 已知 的半径为 ,点P到圆心O的距离为 ,则点 和 的位置关系是( )A、点P在圆内 B、点P在圆上 C、点P在圆外 D、不能确定3. 用配方法解一元二次方程x2﹣4x+2=0,下列配方正确的是( )A、(x+2)2=2 B、(x﹣2)2=﹣2 C、(x﹣2)2=2 D、(x﹣2)2=64. 二次函数y=x2+4x+3的图象可以由二次函数y=x2的图象平移而得到,下列平移正确的是( )A、先向左平移2个单位,再先向上平移1个单位 B、先向左平移2个单位,再先向下平移1个单位 C、先向右平移2个单位,再先向上平移1个单位 D、先向右平移2个单位,再先向下平移1个单位5. 某种品牌的手机经过四、五月份连续两次降价,每部售价由3200元降到了2500元.设平均每月降价的百分率为x,根据题意列出的方程是( )A、 B、 C、 D、6. 正方形ABCD在坐标系中的位置如图所示,将正方形ABCD绕D点顺时针旋转90°后,B点的坐标为( )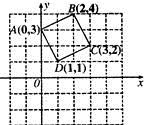 A、(-2,2) B、(4,1) C、(3,1) D、(4,0)7. 抛物线的顶点为 ,与y轴交于点 ,则该抛物线的解析式为( )A、 B、 C、 D、8. 如图,在 中, ,以点 为旋转中心,把 顺时针旋转得 ,记旋转角为 , 为 ,当旋转后满足 时, 与 之间的数量关系为( )
A、(-2,2) B、(4,1) C、(3,1) D、(4,0)7. 抛物线的顶点为 ,与y轴交于点 ,则该抛物线的解析式为( )A、 B、 C、 D、8. 如图,在 中, ,以点 为旋转中心,把 顺时针旋转得 ,记旋转角为 , 为 ,当旋转后满足 时, 与 之间的数量关系为( )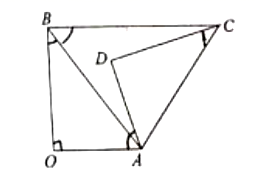 A、 B、 C、 D、9. 如图, 是 的直径,A,B,C是 上的三点, , B点是 的中点,P点是 上一动点,若 的半径为1,则 的最小值为( )
A、 B、 C、 D、9. 如图, 是 的直径,A,B,C是 上的三点, , B点是 的中点,P点是 上一动点,若 的半径为1,则 的最小值为( )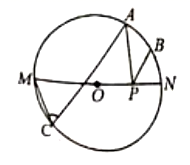 A、1 B、 C、 D、10. 二次函数 中(b,c是常数)的自变量x与函数值y的部分对应值如下表:
A、1 B、 C、 D、10. 二次函数 中(b,c是常数)的自变量x与函数值y的部分对应值如下表:……
0
1
2
3
4
……
……
10
5
2
1
2
5
……
下列结论正确的是( )
A、当 时,y有最大值1 B、当 时,y随x的增大而增大 C、点 在该函数的图象上 D、若 , 两点都在该函数的图象上,则当 时, .11. 已知关于x的一元二次方程 与 ,下列判断错误的是( )A、若方程 有两个实数根,则方程 也有两个实数根; B、如果m是方程 的一个根,那么 是 的一个根; C、如果方程 与 有一个根相等,那么这个根是1; D、如果方程 与 有一个根相等,那么这个根是1或-1.12. 在平面直角坐标系中,若点P的橫坐标和纵坐标相等,则称点P为完美点,已知二次函数 (a,b是常数, )的图象上有且只有一个完美点 ,且当 时,函数 的最小值为 ,最大值为1,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 方程 的一次项系数是 .14. 点 关于原点对称的点坐标是 .15. 如图,A,B是 上的两点 ,C是 的中点,则 的大小(度).
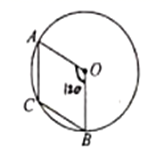 16. 已知抛物线 与 轴交于 两点,若点 的坐标为 ,抛物线的对称轴为直线 ,则点 的坐标为 .17. 如图, 内接于 , , 是 的中点,且 , , 分别是 , 边上的高,则 的大小 (度).
16. 已知抛物线 与 轴交于 两点,若点 的坐标为 ,抛物线的对称轴为直线 ,则点 的坐标为 .17. 如图, 内接于 , , 是 的中点,且 , , 分别是 , 边上的高,则 的大小 (度). 18. 已知抛物线 .(1)、该抛物线的对称轴是 .(2)、该抛物线与x轴交于点A,点B与y轴交于点C,点A的坐标为 ,若此抛物线的对称轴上的点P满足 ,则点P的纵坐标n的取值范围是.
18. 已知抛物线 .(1)、该抛物线的对称轴是 .(2)、该抛物线与x轴交于点A,点B与y轴交于点C,点A的坐标为 ,若此抛物线的对称轴上的点P满足 ,则点P的纵坐标n的取值范围是.三、解答题
-
19.(1)、 ;(2)、 .20. 如图, 是 的直径, 平分弦 ,交 于点E, , .求 的长.
 21.
21.已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
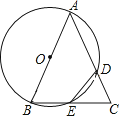 (1)、求证:AB=AC;(2)、若AB=4,BC=2 ,求CD的长.22. 一个矩形周长为56厘米.(1)、当矩形面积为180平方厘米时,长宽分别为多少?(2)、能围成面积为200平方米的矩形吗?请说明理由.23. 俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.(1)、请直接写出y与x之间的函数关系式和自变量x的取值范围;
(1)、求证:AB=AC;(2)、若AB=4,BC=2 ,求CD的长.22. 一个矩形周长为56厘米.(1)、当矩形面积为180平方厘米时,长宽分别为多少?(2)、能围成面积为200平方米的矩形吗?请说明理由.23. 俄罗斯世界杯足球赛期间,某商店销售一批足球纪念册,每本进价40元,规定销售单价不低于44元,且获利不高于30%.试销售期间发现,当销售单价定为44元时,每天可售出300本,销售单价每上涨1元,每天销售量减少10本,现商店决定提价销售.设每天销售量为y本,销售单价为x元.(1)、请直接写出y与x之间的函数关系式和自变量x的取值范围;
(2)、当每本足球纪念册销售单价是多少元时,商店每天获利2400元?
(3)、将足球纪念册销售单价定为多少元时,商店每天销售纪念册获得的利润w元最大?最大利润是多少元?
24. 在 中, ,M是平面内任意一点,将线段 绕点A顺时针旋转与 相等的角度,得到线段 ,连接 .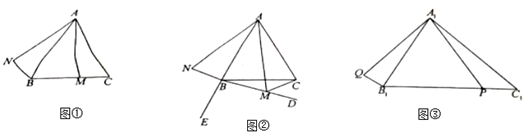 (1)、如图①,若M是线段 上的一点,且 , ,则 的大小 (度), 的长 ;(2)、如图②,点E是 延长线上的一点,若M是 内部射线 上任意一点,连接 , 与 的数量关系是什么? 与 的数量关系是什么?并分别给予证明:(3)、如图③,在 中, , , , 是 上的任意一点,连接 ,将 绕点 顺时针旋转 ,得到线段 ,连接 ,求线段 长度的最小值(直接写出结果即可).25. 在平面直角坐标系中,点O为坐标原点,抛物线 经过点 和 .(1)、求该抛物线的解析式及顶点坐标;(2)、把该抛物线向(填“上”或“下”)平移个单位长度,得到的抛物线与x轴只有一个公共点;(3)、平移该抛物线,使平移后的抛物线经过点 ,且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.
(1)、如图①,若M是线段 上的一点,且 , ,则 的大小 (度), 的长 ;(2)、如图②,点E是 延长线上的一点,若M是 内部射线 上任意一点,连接 , 与 的数量关系是什么? 与 的数量关系是什么?并分别给予证明:(3)、如图③,在 中, , , , 是 上的任意一点,连接 ,将 绕点 顺时针旋转 ,得到线段 ,连接 ,求线段 长度的最小值(直接写出结果即可).25. 在平面直角坐标系中,点O为坐标原点,抛物线 经过点 和 .(1)、求该抛物线的解析式及顶点坐标;(2)、把该抛物线向(填“上”或“下”)平移个单位长度,得到的抛物线与x轴只有一个公共点;(3)、平移该抛物线,使平移后的抛物线经过点 ,且与y轴交于点B,同时满足以A,O,B为顶点的三角形是等腰直角三角形,请你写出平移过程,并说明理由.