四川省遂宁市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-23 类型:期末考试
一、单选题
-
1. 下列各式中,分式的个数为( )
, , , , , ,
A、2个 B、3个 C、4个 D、5个2. 如果分式 的值为0,那么 的值为( )A、 B、 C、 或 D、3或03. 下列分式中,是最简分式的是( )A、 B、 C、 D、4. 若点M(m+3,m﹣2)在x轴上,则点M的坐标为( )A、(0,﹣5) B、(0,5) C、(﹣5,0) D、(5,0)5. 计算 =( )A、5 B、﹣3 C、 D、6. 方程 的解为( )A、x=1 B、x=2 C、x=3 D、x=47. 若关于 的分式方程 有增根,则 的值是( )A、 B、 C、 D、8. 下列图象能表示y是x的函数的是( )A、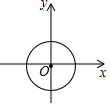 B、
B、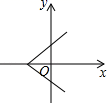 C、
C、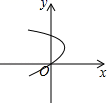 D、
D、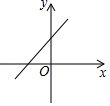 9. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、 且10. 研究表明,某新型冠状病毒体大小约为125纳米也就是0.125微米,而95口罩能过滤0.3微米的颗粒,并不能将病毒过滤,口罩的作用是阻挡病毒传播的“载体”,而非直接挡住病毒.1纳米就是0.000000001米.那么0.3微米用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米11. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中 表示时间, 表示林茂离家的距离。依据图中的信息,下列说法错误的是( )
9. 函数 的自变量 的取值范围是( )A、 B、 C、 且 D、 且10. 研究表明,某新型冠状病毒体大小约为125纳米也就是0.125微米,而95口罩能过滤0.3微米的颗粒,并不能将病毒过滤,口罩的作用是阻挡病毒传播的“载体”,而非直接挡住病毒.1纳米就是0.000000001米.那么0.3微米用科学记数法表示为( )A、 米 B、 米 C、 米 D、 米11. 已知林茂的家、体育场、文具店在同一直线上,图中的信息反映的过程是林茂从家跑步去体育场,在体育场锻炼了一阵后又走到文具店买笔,然后再走回家,图中 表示时间, 表示林茂离家的距离。依据图中的信息,下列说法错误的是( )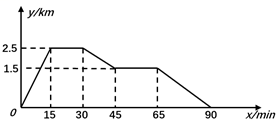 A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min12. 已知直线 y=-3x+4 过点 A(-1,y1)和点(-3,y2),则 y1 和 y2 的大小关系是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定13. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为6,则k的值是( )
A、体育场离林茂家2.5km B、体育场离文具店1km C、林茂从体育场出发到文具店的平均速度是50m/min D、林茂从文具店回家的平均速度是60m/min12. 已知直线 y=-3x+4 过点 A(-1,y1)和点(-3,y2),则 y1 和 y2 的大小关系是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定13. 如图,点A是反比例函数y= 的图象上的一点,过点A作AB⊥x轴,垂足为B.点C为y轴上的一点,连接AC,BC.若△ABC的面积为6,则k的值是( )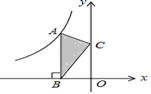 A、6 B、﹣6 C、12 D、﹣1214. 已知 的周长为32cm,对角线 、 相交于点O,若 的周长比 的周长大4cm,则 的长是( ).A、4cm B、6cm C、8cm D、10cm15. 如图,在四边形ABCD中,对角线AC,BD交于点O,下列选项不能得到四边形ABCD是平行四边形的是( )
A、6 B、﹣6 C、12 D、﹣1214. 已知 的周长为32cm,对角线 、 相交于点O,若 的周长比 的周长大4cm,则 的长是( ).A、4cm B、6cm C、8cm D、10cm15. 如图,在四边形ABCD中,对角线AC,BD交于点O,下列选项不能得到四边形ABCD是平行四边形的是( )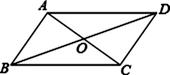 A、AC=BD,OA=OC B、OB=OD,OA=OC C、AD=BC,AD∥BC D、△ABC≌△CDA16. 下列性质中,矩形具有而菱形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边相等17. 如图,矩形ABCD中,AB=8cm,点E在AD上,且AE=4cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点 处,则BC的值为( )
A、AC=BD,OA=OC B、OB=OD,OA=OC C、AD=BC,AD∥BC D、△ABC≌△CDA16. 下列性质中,矩形具有而菱形不一定具有的是( )A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、邻边相等17. 如图,矩形ABCD中,AB=8cm,点E在AD上,且AE=4cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点 处,则BC的值为( )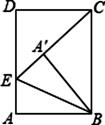 A、8cm B、6cm C、12cm D、10cm18. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )
A、8cm B、6cm C、12cm D、10cm18. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )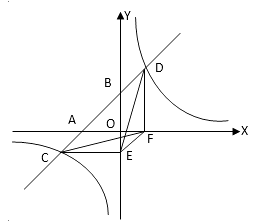 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
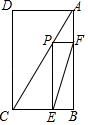
19. 分式 , , 的最简的分母是.20. 在平面直角坐标系中,点A(2,﹣3)与点B(2,3)关于轴对称.21. 已知方程 ,如果设 ,那么原方程可以变形成关于 的方程为 .22. 已知关于 的方程 的解是正数,则 的取值范围为.23. 如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为 .
 24. 已知菱形OABC在坐标系中如图放置,点C在x轴上,若点A坐标为(6,8),经过A点的双曲线交BC于D,则△OAD的面积为 .
24. 已知菱形OABC在坐标系中如图放置,点C在x轴上,若点A坐标为(6,8),经过A点的双曲线交BC于D,则△OAD的面积为 .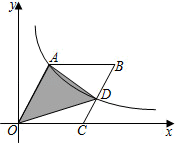
三、解答题
-
25. 计算:(﹣ )﹣2+4×(﹣1)2019﹣|﹣23|+(π﹣5)026. 解方程: .27. 先化简,再从a=-1,1,2中选一个恰当的数求值, ,28. 2020年新冠肺炎疫情影响全球,各国感染人数持续攀升,医用口罩供不应求,很多企业纷纷加入生产口罩的大军中来,邵阳某企业临时增加甲、乙两个厂房生产口罩,甲厂房每天生产的数量是乙厂房每天生产数量的1.5倍,两厂房各加工6000箱口罩,甲厂房比乙厂房少用5天.(1)、求甲、乙两厂房每天各生产多少箱口罩;(2)、已知甲、乙两厂房生产这种口罩每天的生产费分别是1500元和1200元,现有30000箱口罩的生产任务,甲厂房单独生产一段时间后另有安排,剩余任务由乙厂房单独完成.如果总生产费不超过81000元,那么甲厂房至少生产了多少天?29. 如图,在 中,E、F是对角线AC上的两点,AE=CF.
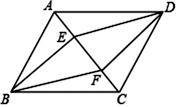 (1)、求证:四边形BEDF是平行四边形;(2)、连接BD交EF于点O,当BE⊥EF且BE=8,BF=10时,求BD的长.30. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.
(1)、求证:四边形BEDF是平行四边形;(2)、连接BD交EF于点O,当BE⊥EF且BE=8,BF=10时,求BD的长.30. 如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于E,CF∥AE交AD延长线于点F.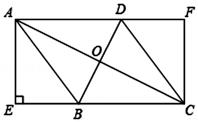 (1)、求证:四边形AECF是矩形;(2)、连接OE,若AD=5,BE=3,求线段OE的长.31. 如图,直线y=kx+b与反比例函数 的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C , D .
(1)、求证:四边形AECF是矩形;(2)、连接OE,若AD=5,BE=3,求线段OE的长.31. 如图,直线y=kx+b与反比例函数 的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C , D .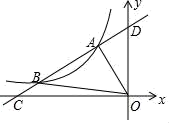 (1)、求此一次函数和反比例函数的解析式;(2)、求△AOB的面积.32. 如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.
(1)、求此一次函数和反比例函数的解析式;(2)、求△AOB的面积.32. 如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.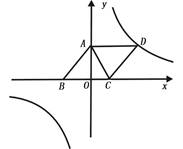 (1)、证明:四边形ABCD为菱形;(2)、求此反比例函数的解析式;(3)、设过点C和点D的一次函数y=kx+b,求不等式kx+b﹣ >0的解.(请直接写出当 时的答案);(4)、已知在y= 的图象上一点N,y轴上一点M,且点A、B、M、N组成四边形是平行四边形,求M点的坐标.
(1)、证明:四边形ABCD为菱形;(2)、求此反比例函数的解析式;(3)、设过点C和点D的一次函数y=kx+b,求不等式kx+b﹣ >0的解.(请直接写出当 时的答案);(4)、已知在y= 的图象上一点N,y轴上一点M,且点A、B、M、N组成四边形是平行四边形,求M点的坐标.