四川省内江市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-23 类型:期末考试
一、单选题
-
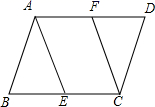
1. 下列式子中是分式的是( )A、 B、 C、 D、2. 若点 位于第一象限,则点 在( )A、第四象限 B、第三象限 C、第二象限 D、第一象限3. 在▱ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是
 A、 B、 C、 D、4. 下列性质中,为菱形所具备而平行四边形却不一定具有的是( )A、对角线互相平分 B、对角线相等 C、邻角相等 D、邻边相等5. 小欣同学对数据28,2■,48,50,52进行统计分析,发现其中一个两位数的个位数字被墨水污染看不到了,则分析结果与被污染数字无关的是( )A、平均数 B、方差 C、中位数 D、众数6. 在同一直角坐标系中,函数y=kx﹣k与y= (k≠0)的图象大致是( )A、
A、 B、 C、 D、4. 下列性质中,为菱形所具备而平行四边形却不一定具有的是( )A、对角线互相平分 B、对角线相等 C、邻角相等 D、邻边相等5. 小欣同学对数据28,2■,48,50,52进行统计分析,发现其中一个两位数的个位数字被墨水污染看不到了,则分析结果与被污染数字无关的是( )A、平均数 B、方差 C、中位数 D、众数6. 在同一直角坐标系中,函数y=kx﹣k与y= (k≠0)的图象大致是( )A、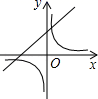 B、
B、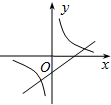 C、
C、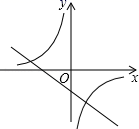 D、
D、 7. 若关于x的方程 1的解为正数,则所有符合条件的正整数a的个数为( )A、1个 B、2个 C、3个 D、4个8. 如图,平行四边形ABCD中, , ,沿直线DE将 翻折,使点A落在点 处, 交BD于点F,则 ( )
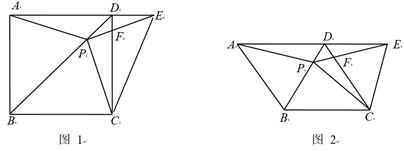
7. 若关于x的方程 1的解为正数,则所有符合条件的正整数a的个数为( )A、1个 B、2个 C、3个 D、4个8. 如图,平行四边形ABCD中, , ,沿直线DE将 翻折,使点A落在点 处, 交BD于点F,则 ( ) A、 B、 C、 D、9. 若点A(x1 , 1)、B(x2 , ﹣2)、C(x3 , ﹣3)在反比例函数y=﹣ 的图象上,则x1、x2、x3的大小关系是( )A、x1<x2<x3 B、x1<x3<x2 C、x3<x1<x2 D、x2<x1<x310. 如图1,在菱形 中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x, 的面积为y.把y看作x的函数,函数的图象如图2所示,则图2中的a等于( )
A、 B、 C、 D、9. 若点A(x1 , 1)、B(x2 , ﹣2)、C(x3 , ﹣3)在反比例函数y=﹣ 的图象上,则x1、x2、x3的大小关系是( )A、x1<x2<x3 B、x1<x3<x2 C、x3<x1<x2 D、x2<x1<x310. 如图1,在菱形 中,动点P从点B出发,沿折线B→C→D→B运动,设点P经过的路程为x, 的面积为y.把y看作x的函数,函数的图象如图2所示,则图2中的a等于( )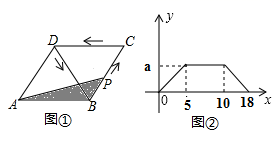 A、25 B、20 C、12 D、11. 如图,反比例函数 的图象与矩形ABCO的边AB、BC相交于E、F两点,点A、C在坐标轴上.若 ,则四边形OEBF的面积为( )
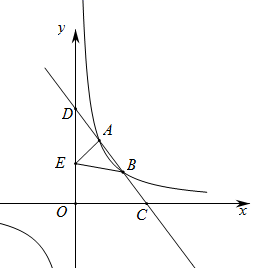
A、25 B、20 C、12 D、11. 如图,反比例函数 的图象与矩形ABCO的边AB、BC相交于E、F两点,点A、C在坐标轴上.若 ,则四边形OEBF的面积为( )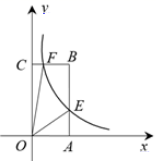 A、1 B、2 C、3 D、412. 如图所示,已知点C(2,0),直线 与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,当 的周长取最小值时,点D的坐标为( )
A、1 B、2 C、3 D、412. 如图所示,已知点C(2,0),直线 与两坐标轴分别交于A、B两点,D、E分别是AB、OA上的动点,当 的周长取最小值时,点D的坐标为( )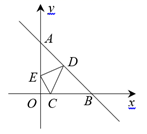 A、(2,1) B、(3,2) C、( ,2) D、( , )
A、(2,1) B、(3,2) C、( ,2) D、( , )二、填空题
-
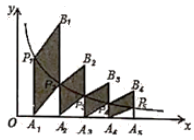
13. 根据测算,1粒芝麻重0.000004克,数0.000004可用科学记数法表示为 .14. 数据6,5,x,4,7的平均数是5,那么这组数据的方差为;15. 在菱形 中, ,两条对角线 与 的和是22.则菱形 的面积是 .16. 如图,分别过反比例函数 图象上的点 , ... ···作 轴的垂线,垂足分别为 ······ ,连接 ··· 再以 为一组邻边画一个平行四边形 ,以 为一组邻边画一个平行四边形 ,依此类推,则点 的纵坐标是 . (结果用含 代数式表示)
三、解答题
-
17.(1)、计算:(2)、先化简,再求值: ,其中18. 如图,在平行四边形ABCD中,E、F分别是DA、BC延长线上的点,且∠ABE=∠CDF.
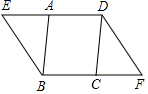
求证:
(1)、△ABE≌△CDF;(2)、四边形EBFD是平行四边形.19. 某中学为了抗疫宣传,在七、八年级开展了“防疫知识”大赛.为了解参赛学生的成绩情况,从两个年级各随机抽取10名学生的成绩,数据如下:七年级:88 94 90 94 84 94 99 94 99 100
八年级:84 93 88 94 93 98 93 98 97 99
整理数据:按如下分段整理样本数据并补全表格:
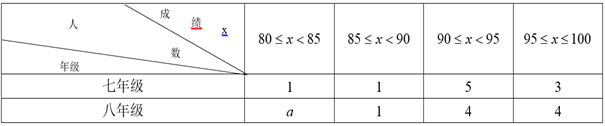
分析数据:补全下列表格中的统计量:

得出结论:
(1)、a=;b=;c=;(2)、由统计数据可知,年级选手的成绩比较接近;(3)、学校规定,成绩不低于90分的选手可以获奖,若该校七年级有200人参加比赛,请估计有多少人获奖?20. 为提升青少年的身体素质,某市在全市中小学推行“阳光体育”活动,某实验中学为满足学生的需求,准备再购买一些篮球和足球.如果分别用800元购买篮球和足球,购买篮球的个数比足球的个数少2个,已知足球的单价为篮球单价的 .(1)、求篮球、足球的单价分别为多少元?(2)、学校计划购买篮球、足球共60个,如果购买足球m个,总费用为w元,请写出w与m的函数关系式;(3)、在(2)的条件下学校计划总费用不多于5200元,并且要求篮球数量不能低于15个,那么应如何安排购买方案才能使费用最少,最少费用应为多少?