四川省绵阳市三台县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-23 类型:期末考试
一、单选题
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 下列运算正确的是( )A、 B、3 =3 C、 =﹣2 D、3. 一次函数y=4x﹣2的图象可以由正比例函数y=4x的图象( )得到.A、向上平移2个单位 B、向下平移4个单位 C、向下平移2个单位 D、向上平移4个单位4. 下列哪个点在函数 的图象上( )A、 B、 C、 D、5. 下列性质中,菱形具有而平行四边形不具有的性质是( )A、对边平行且相等 B、对角线互相平分 C、每条对角线平分一组对角 D、对角互补6. 下列各图中,表示y是x的函数的是( )A、
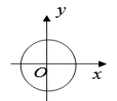 B、
B、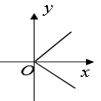 C、
C、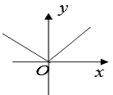 D、
D、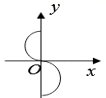 7. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )
7. 如图,在▱ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD,交AD于点E,若AB=6,EF=2,则BC的长为( )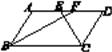 A、8 B、10 C、12 D、148. 如图,直角三角形两直角边的长分别为3和4,以直角三角形的两直边为直径作半圆,则阴影部分的面积是( )
A、8 B、10 C、12 D、148. 如图,直角三角形两直角边的长分别为3和4,以直角三角形的两直边为直径作半圆,则阴影部分的面积是( )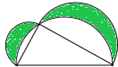 A、6 B、 C、2π D、129. 如图,顺次连接四边形ABCD各边的中点,得到四边形EFGH,在下列条件中,可使四边形 EFGH 成为菱形的是( )
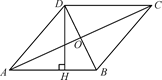
A、6 B、 C、2π D、129. 如图,顺次连接四边形ABCD各边的中点,得到四边形EFGH,在下列条件中,可使四边形 EFGH 成为菱形的是( ) A、AB=CD B、AC=BD C、AC⊥BD D、AD//BC10. 如图,已知O是矩形ABCD的对角线的交点,∠AOB=60°,作DE∥AC,CE∥BD,DE、CE相交于点E.四边形OCED的周长是20,则BC=( )
A、AB=CD B、AC=BD C、AC⊥BD D、AD//BC10. 如图,已知O是矩形ABCD的对角线的交点,∠AOB=60°,作DE∥AC,CE∥BD,DE、CE相交于点E.四边形OCED的周长是20,则BC=( )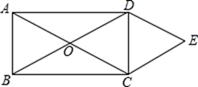 A、5 B、5 C、10 D、1011. 如图,在 中,点 分别在边 , , 上,且 , .下列四个判断中,错误的是( )
A、5 B、5 C、10 D、1011. 如图,在 中,点 分别在边 , , 上,且 , .下列四个判断中,错误的是( )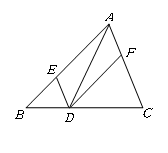 A、四边形 是平行四边形 B、如果 ,那么四边形 是矩形 C、如果 平分平分∠BAC,那么四边形 AEDF 是菱形 D、如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形12. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123;④乙的速度比甲的速度快1米/秒,其中正确的编号是( )
A、四边形 是平行四边形 B、如果 ,那么四边形 是矩形 C、如果 平分平分∠BAC,那么四边形 AEDF 是菱形 D、如果AD⊥BC 且 AB=AC,那么四边形 AEDF 是正方形12. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123;④乙的速度比甲的速度快1米/秒,其中正确的编号是( )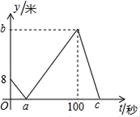 A、①② B、②③ C、①②③ D、①②③④
A、①② B、②③ C、①②③ D、①②③④二、填空题
-
13. 使式子 有意义的x的取值范围是 .14. 计算: = .15. 如图,四边形ABCD是菱形,AC=16,DB=12,DH⊥AB于点H,则DH等于 .
 16. 函数y=kx与y=6﹣x的图象如图所示,则不等式6﹣x≥kx的解集为 .
16. 函数y=kx与y=6﹣x的图象如图所示,则不等式6﹣x≥kx的解集为 .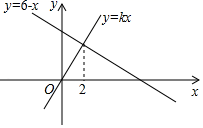 17. 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD= BC,连接DM,DN,MN,若AB=6,则DN= .
17. 如图,在△ABC中,∠ACB=90°,M,N分别是AB,AC的中点,延长BC至点D,使CD= BC,连接DM,DN,MN,若AB=6,则DN= .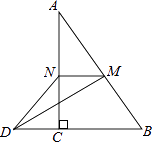 18. 如图,直线 与 轴、 轴分别交于 ,将△ 沿过点 的直线折叠,使点 落 轴正半轴的 点,折在痕与 轴交于点 ,则折痕所在直线的解析式为.
18. 如图,直线 与 轴、 轴分别交于 ,将△ 沿过点 的直线折叠,使点 落 轴正半轴的 点,折在痕与 轴交于点 ,则折痕所在直线的解析式为.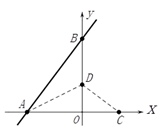
三、解答题
-
19.(1)、计算:(2)、已知a、b、c满足 .判断以a、b、c为边能否构成三角形?若能构成三角形,说明此三角形是什么形状?并求出三角形的面积;若不能,请说明理由.20. 某校八年级一班要从平时在班级里数学比较优秀的甲、乙两位同学中选拔一人参加“全国初中数学联赛”,为此对两位同学进行了辅导,并在辅导期间进行了6次测验,两位同学测验成绩记录如下表:
第1次
第2次
第3次
第4次
第5次
第6次
甲
79
78
86
82
81
78
乙
82
80
80
83
80
75
利用表中提供的数据,解答下列问题:
(1)、填写完成表格;平均成绩
中位数
众数
甲
80
80
乙
80
80
(2)、老师从测验成绩记录表中,求得甲的方差是8.33,请你计算出乙的方差.你认为老师应该派哪位同学参赛?21. 如图,在▱ABCD中,点E,F分别是边AD,BC的中点,求证:AF=CE.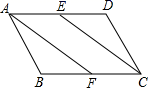 22. 如图,在Rt ABC中,∠ACB=90°.过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC交直线m于点E,垂足为点F,连结CD、BE.
22. 如图,在Rt ABC中,∠ACB=90°.过点C的直线m∥AB,D为AB边上一点,过点D作DE⊥BC交直线m于点E,垂足为点F,连结CD、BE.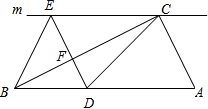 (1)、求证:CE=AD(2)、当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若点D是AB中点,当四边形BECD是正方形时,则∠A大小满足什么条件?23. 已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设 OBA的面积为S.
(1)、求证:CE=AD(2)、当点D是AB中点时,四边形BECD是什么特殊四边形?说明你的理由;(3)、若点D是AB中点,当四边形BECD是正方形时,则∠A大小满足什么条件?23. 已知点A(8,0)及在第一象限的动点B(x,y),且x+y=10,设 OBA的面积为S.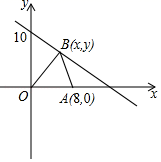 (1)、求S关于x的函数关系式,并写出自变量x的取值范围;(2)、求S=12时B点坐标;(3)、在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.24. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:
(1)、求S关于x的函数关系式,并写出自变量x的取值范围;(2)、求S=12时B点坐标;(3)、在(2)的基础上,设点Q为y轴上一动点,当BQ+AQ的值最小时,求Q点坐标.24. 为了贯彻落实市委政府提出的“精准扶贫”精神,某校特制定了一系列帮扶A、B两贫困村的计划,现决定从某地运送152箱鱼苗到A、B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A、B两村的运费如表:车型 目的地 A村(元/辆) B村(元/辆) 大货车 800 900 小货车 400 600
(1)、求这15辆车中大小货车各多少辆?(2)、现安排其中10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A、B两村总费用为y元,试求出y与x的函数解析式.(3)、在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.