四川省泸州市泸县2019-2020学年八年级下学期数学期末试卷
试卷更新日期：2020-09-23 类型：期末考试
一、单选题
-
1. 下列式子为最简二次根式的是（ ）A、 B、 C、 D、2. 在下列条件中，不能判定四边形为平行四边形的是（ ）A、对角线互相平分 B、一组对边平行且相等 C、两组对边分别平行 D、一组对边平行，另一组对边相等3. 式子 在实数范围内有意义，则x的取值范围是（ ）A、x≥5 B、x＞﹣5 C、x≥﹣5 D、x＞54. 一次函数y=﹣2x+1的图象不经过（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 在△ABC中，BC＝5，AC＝4，AB＝3，则（ ）A、∠A＝90° B、∠B＝90° C、∠C＝90° D、∠A+∠B＝90°6. 如图，在△ABC中，点D，E，F分别是边AB，AC，BC的中点，已知∠A＝65°，则∠DFE＝（ ）
A、60° B、62° C、64° D、65°7. 要得到函数y＝2x﹣3的图象，只需将函数y＝2x的图象（ ）A、向左平移3个单位 B、向右平移3个单位 C、向上平移3个单位 D、向下平移3个单位8. 国家实行“精准扶贫”政策后，农民收入大幅度增加．某镇所辖5个村去年的年人均收入（单位：万元）为：1.5，1.7，1.8，1.2，1.9，该镇各村去年年人均收入的中位数是（ ）A、1.2万元 B、1.7万元 C、1.8万元 D、1.5万元9. 如图，在正方形ABCD中，E为对角线BD上一点，且BE＝BC，则∠ACE＝（ ）
A、20.5° B、30.5° C、21.5° D、22.5°10. 如图，直线y=ax+b过点A（0，2）和点B（﹣3，0），则方程ax+b=0的解是（ ）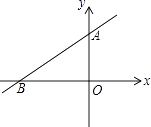
A、x=2 B、x=0 C、x=﹣1 D、x=﹣311. 如图，矩形ABCD的对角线AC，BD相交于点O，AD＝3，∠AOD＝60°，则AB的长为（ ）
A、3 B、2 C、3 D、612.如图，矩形ABCD中，AB＝1，AD＝2，M是CD的中点，点P在矩形的边上沿A⇒B⇒C⇒M运动，则△APM的面积y与点P经过的路程x之间的函数关系用图象表示大致是下图中的（ ）
A、
B、
C、 
D、
二、填空题
-
13. 计算﹣ 的结果是 ．14. 一组数据，1，3，2，5，x的平均数为3，那么这组数据的标准差是 ．15. 已知，函数y＝3x+b的图象经过点A（﹣1，y1），点B（﹣2，y2），则y1y2（填“＞”“＜”或“＝”）16. 将一根长24cm的筷子置于底面直径为5cm、高为12cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长为h cm， 则h的取值范围是.
三、解答题
-
17. 计算： ×（ ﹣4 ）．18. 如图，E是▱ABCD的边AB的中点，连接CE并延长交DA的延长线于F，若BC＝8，求DF的长．
19. 已知x＝ + ，y＝ ﹣ ，求x2﹣y2的值．20. 一次函数y＝kx+b的图象经过M（0，2），N（1，3）两点．
(1)、求一次函数的解析式；(2)、画出y＝kx+b的图象，并根据图象写出当kx+b≥0时x的范围．21. 某校以“绅士风度，淑女气质”为主题文化，一天，观察员以不亮身份的方式对全校7个班“乱扔垃圾的人次”作记录，数据统计如图：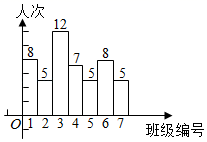
(1)、求各班“乱扔垃圾的人次”的中位数和众数；(2)、计算这一天班级“乱扔垃圾的人次”的平均数（结果保留1位小数）．22. 《九章算术》中有“折竹抵地”问题：今有竹高一丈，末折抵地，去根七尺，问折高者几何？意思是：一根竹子，原高一丈（一丈＝10尺），一阵风将竹子折断，其竹稍恰好抵地，抵地处距竹子底端7尺远，问折断处离地面的高度是多少尺？
23. 在Rt△ABC中，∠BAC=90°，D是BC的中点，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．
(1)、求证：AF=BD．(2)、求证：四边形ADCF是菱形．24. 某长途汽车客运公司规定旅客可免费携带一定质量的行李，如果行李的质量超过规定时，则需要付行李费，行李费y（元）是行李质量x（kg）的一次函数．当行李质量为60kg时，行李费为6元；当行李质量为90kg时，行李费为15元．(1)、当行李的质量x超过规定时，求出y与x之间的函数关系式；(2)、求旅客最多可免费携带的行李质量．25. 如图，在△ABC中，点D、E分别是边AB、AC的中点，连接DE、BE，已知O为BE的中点，连接DO并延长交BC边于点F，连接EF．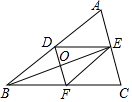
(1)、求证：四边形BDEF为平行四边形；(2)、设BE＝m，DF＝n，BD＝a，BF＝b，求证：m2+n2＝2a2+2b2 ．