四川省成都市青羊区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图案中，既是中心对称图形又是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列多项式分解因式正确的是（）

A、a²﹣2a﹣3＝a（a﹣2）﹣3 B、3ax²﹣6ax＝3（ax²﹣2ax） C、m³﹣m＝m（m﹣1）（m＋1） D、x²＋2xy﹣y²＝（x﹣y）²

查看试题解析
3. 在平面直角坐标系中，点P（﹣2，3）向右平移3个单位长度后的坐标为（）

A、（3，6） B、（1，3） C、（1，6） D、（6，6）

查看试题解析
4. 若关于 $x$ 的不等式 $(m - 1) x > m - 1$ 的解集是 $x < 1$ ，则m的取值范围是（）

A、 $m \neq 1$ B、m＞1 C、m＜1 D、 $m$ 为任何实数

查看试题解析
5. 内角和为1800°的多边形是（）

A、十二边形 B、十边形 C、八边形 D、七边形

查看试题解析
6. 下列各式从左到右的变形，一定正确的是（）

A、 $\frac{- b + c}{a}$ ＝﹣ $\frac{b + c}{a}$ B、 $\frac{a - 0.3 b}{a + 0.2 b}$ ＝ $\frac{a - 3 b}{a + 2 b}$ C、 $\frac{b}{a}$ ＝ $\frac{b + 1}{a + 1}$ D、 $\frac{a^{2} - 9}{{(a + 3)}^{2}}$ ＝ $\frac{a - 3}{a + 3}$

查看试题解析
7. 若解关于x的分式方程 $\frac{2 x + m}{x - 2}$ ＝1时出现了增根，则m的值为（）

A、﹣4 B、﹣2 C、4 D、2

查看试题解析
8. 如图，菱形ABCD边长为5cm，P为对角线BD上一点，PH⊥AB于点H，且PH＝2cm，则△PBC的面积为（）cm² ．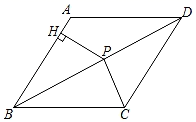

A、8 B、7 C、6 D、5

查看试题解析
9. 如图，在△ABC中，∠BAC＝90°，BD平分∠ABC，CD∥AB交BD于点D，已知∠ACB＝34°，则∠D的度数为（）

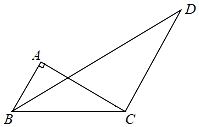A、30° B、28° C、26° D、34°

查看试题解析
10. 如图，若一次函数y＝﹣2x＋b的图象与两坐标轴分别交于A，B两点，点A的坐标为(0，4)，则不等式﹣2x＋b＜0的解集为（）

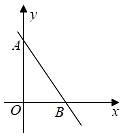A、x＞2 B、x＜2 C、x＜4 D、x＞4

查看试题解析

二、填空题

11. 若x²＋mx＋ $\frac{9}{4}$ ＝（x﹣ $\frac{3}{2}$ ）² ，则m＝．

查看试题解析
12. 若分式 $\frac{x (x + 2)}{x}$ 的值为0，则x＝．

查看试题解析
13. 如图，在等腰Rt△ABC中，∠C＝90°，D为AC边上任意一点，作BD的垂直平分线交AB于点E，交BC于点F．连接DE、DF，当BC＝1时，△ADE与△CDF的周长之和为．

查看试题解析
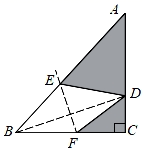14. 如图，▱ABCD中，∠B＝60°，AB＝4，AE⊥BC于E，F为边CD上一动点，连接AF、EF，点G，H分别为AF、EF的中点，则GH的长为．

查看试题解析
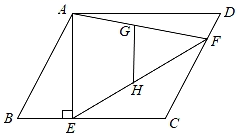15. 若x﹣2y＝3，xy＝1，则2x²y﹣4xy²＝．

查看试题解析
16. 若关于x的分式方程 $\frac{2 x - a}{x - 2}$ ＝ $\frac{1}{3}$ 的解为非负数，则实数a的取值范围是．

查看试题解析
17. 已知关于x的不等式组 ${\begin{array}{l} x - a < 0 \\ 9 - 2 x \leq 3 \end{array}$ 有且只有2个整数解，且a为整数，则a的值为．

查看试题解析
18. 如图，正方形ABCD边长为2，F为BC上一动点，作DE⊥AF于E，连接CE．当△CDE是以CD为腰的等腰三角形时，DE的长为．

查看试题解析
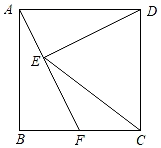19. 如图，在矩形ABCD中，AB＝2，AD＝3，E为BC边上一动点，作EF⊥AE，且EF＝AE．连接DF，AF．当DF⊥EF时，△ADF的面积为．

查看试题解析

三、解答题

20.

(1)、解不等式组： ${\begin{array}{l} 2 (x + 2) ⩽ 3 x + 5 \\ \frac{x}{3} < \frac{x + 1}{4} \end{array}$ ；

(2)、解分式方程： $\frac{1}{x - 2}$ ＝ $\frac{1 - x}{2 - x}$ ﹣3．

查看试题解析
21. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x + 1}$ ÷（x﹣1﹣ $\frac{3}{x + 1}$ ），其中x＝ $\sqrt{3}$ ﹣2．

查看试题解析
22. △ABC在平面直角坐标系中如图：

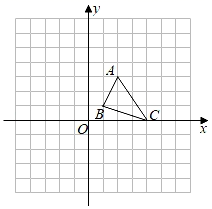(1)、画出将△ABC绕点O逆时针旋转90°所得到的△A₁B₁C₁ ，并写出A₁点的坐标；

(2)、画出△A₁B₁C₁关于原点成中心对称的△A₂B₂C₂ ，并直接写出△AA₁A₂的面积．

查看试题解析
23. 如图，在四边形ABCD中，点E和点F是对角线AC上的两点，AE＝CF，DF＝BE，且DF∥BE．

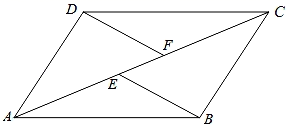(1)、求证：四边形ABCD是平行四边形；

(2)、若∠CEB＝2∠EBA，BE＝3，EF＝2，求AC的长．

查看试题解析
24. 新冠肺炎疫情期间，成都江安河社区有甲、乙两个医疗用品公司，免费为医院加工同种型号的防护服．甲厂每天加工的数量是乙厂每天加工数量的1.5倍，两厂各加工600套防护服，甲厂比乙厂要少用4天．求甲、乙两厂每天各加工多少套防护服？

查看试题解析
25. 如图1，菱形ABCD的对角线AC、BD相交于点O，且AC＝6cm，BD＝8cm，分别过点B、C作AC与BD的平行线相交于点E．

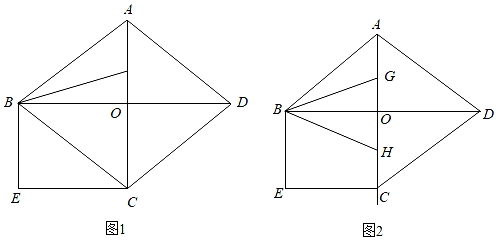(1)、判断四边形BOCE的形状并证明；

(2)、点G从点A沿射线AC的方向以2cm/s的速度移动了t秒，连接BG，当S_△ABG＝2S_△OBG时，求t的值．

(3)、如图2，长度为3cm的线段GH在射线AC上运动，求BG＋BH的最小值．

查看试题解析
26. 某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表：

A种产品

B种产品

成本（万元/件）

2

5

利润（万元/件）

1

3

(1)、若工厂计划获利14万元，问A、B两种产品应分别生产多少件？

(2)、若工厂计划投入资金不多于35万元，且获利多于14万元，问工厂有哪几种生产方案？

(3)、在（2）的条件下，哪种生产方案获利最大？并求出最大利润．

查看试题解析
27. 如图，在正方形ABCD中，对角线AC与BD相交于点O，以B为顶点的等腰Rt△BEF绕点B旋转，连接AF与CE相交于点G，连接DG．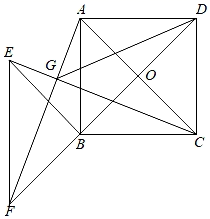

(1)、求证：CE⊥AF；

(2)、求证：AG＋CG＝ $\sqrt{2}$ DG；

(3)、连接CF，当EG∶AG∶FG＝l∶2∶5，且S正方形ABCD＝100时，求DG的长和△BCF的面积．

查看试题解析
28. 如图1，在平面直角坐标系xOy中，已知直线AB：y＝﹣ $\frac{1}{2}$ x＋3与直线CD：y＝kx﹣2相交于点M (4，a)，分别交坐标轴于点A、B、C、D，点P是线段CD延长线上的一个点，△PBM的面积为15．

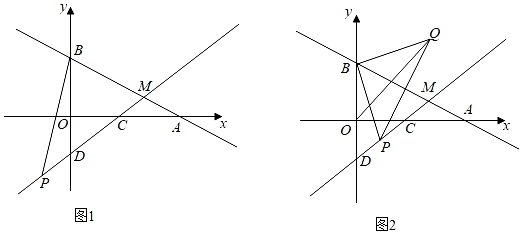(1)、求直线CD解析式和点P的坐标；

(2)、在（1）的条件下，平面直角坐标系内存在点N，使得以点B、N，M、P为顶点的四边形是平行四边形，请直接写出点N的坐标；

(3)、如图2，当点P为直线CD上的一个动点时，将BP绕点B逆时针旋转90°得到BQ，连接PQ与OQ．点Q随着点P的运动而运动，请求出点Q运动所形成直线的解析式，以及OQ的最小值．

查看试题解析

	A种产品	B种产品
成本（万元/件）	2	5
利润（万元/件）	1	3