四川省成都市龙泉驿区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2020-09-23 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 已知a>b，则下列不等式中错误的是（）

A、a+2>b+2 B、a-5<b-5 C、-a<-b D、4a＞4b

查看试题解析
3. 下列各式中，能用平方差公式进行分解因式的是（）

A、x²+y² B、x²﹣2x﹣3 C、x²+2x+1 D、x²﹣4

查看试题解析
4. 函数y= $\frac{\sqrt{x - 2}}{x - 5}$ 中自变量x的取值范围是（）

A、x≥2且x≠5 B、x≥2 C、x≤5 D、x≤2且x≠5

查看试题解析
5. 如果分式 $\frac{x + 3}{x - 2}$ 值为0，那么x的值是（）

A、0 B、2 C、﹣3 D、2或﹣3

查看试题解析
6. 已知一个多边形的内角和是 $720 °$ ，则该多边形的边数为（）

A、4 B、6 C、8 D、10

查看试题解析
7. 疫情期间，为调查某校学生体温的情况，张老师随机调查了50名学生，结果如表：

体温（单位：℃）

36.2

36.3

36.5

36.7

36.8

人数

8

10

7

13

12

则这50名学生体温的众数和中位数分别是（）

A、36.8℃，36.5℃ B、36.8℃，36.7℃ C、36.7℃，36.6℃ D、36.7℃，36.5℃

查看试题解析
8. 关于x的分式方程 $\frac{5}{x - 3} = \frac{2}{x}$ 的解为（）

A、﹣2 B、2 C、﹣3 D、3

查看试题解析
9. 如图，直线a∥b∥c ，分别交直线m ， n于点A ， B ， C ， D ， E ， F ，若AB＝2，BC＝4，DE＝3，则EF的长是（）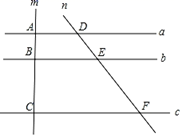

A、5 B、6 C、7 D、8

查看试题解析
10. 如图，Rt△ABC中，∠BAC＝90°，点D ， E分别是边AB ， BC的中点，AD与CE交于点F ，则△DEF与△ACF的面积之比是（）

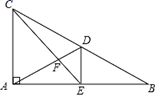A、1：2 B、1：3 C、2：3 D、1：4

查看试题解析

二、填空题

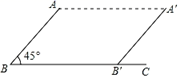
11. 分解因式：x³﹣x= ．

查看试题解析
12. 不等式6﹣2x＞0的解集是．

查看试题解析
13. 已知 $\frac{a}{b} = \frac{3}{4}$ ，那么 $\frac{b}{a + b}$ 的值是．

查看试题解析
14. 如图，已知∠ABC＝45°，AB＝4 $\sqrt{2}$ ，把线段AB向右平移7个单位得到A′B′，则四边形ABB′A′的面积是．

查看试题解析
15. 比较大小： $\frac{\sqrt{5} - 1}{2}$ $\frac{3}{5}$ （填“＞”、“＜”或“=”）

查看试题解析
16. 代数式x²+6x+10的最小值是．

查看试题解析
17. 如图，把Rt△ABC绕点A顺时针旋转35°得到△AB′C′，B′C′与AC相交于点D ， ∠B＝60°，则∠ADB′的度数是．

查看试题解析
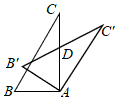18. 如图，在正方形ABCD中，AB＝9，E ， F分别是AB ， CD上的点，连接EF ，将四边形BCFE沿EF折叠得到四边形B′C′FE ，点B′恰好在AD上，若DB′＝2AB′，则折痕EF的长是．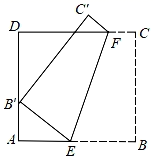

查看试题解析

三、解答题

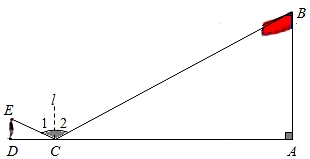
19. 计算：

(1)、分解因式：3x²y﹣12xy²+12y³；

(2)、解不等式组： ${\begin{array}{l} 3 x - 1 > x - 5 ① \\ \frac{x + 2}{3} - x \geq 1 ② \end{array}$ ．

查看试题解析
20. 计算：

(1)、解方程 $\frac{x}{x - 2} = \frac{12}{x^{2} - 4} + 1$ ；

(2)、先化简，再求值： $(\frac{x^{2} + 1}{x^{2} - x} - \frac{2}{x - 1}) \div \frac{x + 1}{x}$ ，其中x＝2．

查看试题解析
21. 某班在学习《利用相似三角形测高》时开展了“测量学校操场上旗杆的高度”的活动．小明将镜子放在离旗杆32m的点C处（即AC＝32m），然后沿直线AC后退，在点D处恰好看到旗杆顶端B在镜子中的像与镜子上的标记重合（如图），根据物理学知识可知：法线l⊥AD ， ∠1＝∠2．若小明的眼睛离地面的高度DE为1.5m ， CD＝3m ，求旗杆AB的高度．（要有证明过程，再求值）

查看试题解析
22. 如图，在▱ABCD中，AB＝4，AD＝9，点E是AD上的一点，AE＝2DE ，延长BE交CD的延长线于F ，求FD的长．

查看试题解析
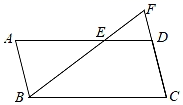23. 在 $R t △ A B C$ 中，∠ACB＝90°，CD⊥AB于点D ，若BD＝9，CD＝12，求AB和AC的长．

查看试题解析
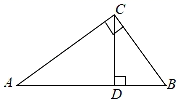24. 如图，在等腰△ABC中，AB＝AC ， ∠BAC＝90°，点D是BC上一点，作AE⊥AD交BC延长线于E ， CF⊥BC交AE于F ．

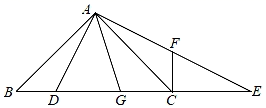(1)、求证：△ABD≌△ACF；

(2)、作AG平分∠DAE交BC于G ，求证：AF²＝DG•DC ．

查看试题解析
25. 如图，在Rt△ABC中，AC＝6，∠C＝90°，∠B＝30°，AD平分∠BAC交BC于点D ，点E为AB上一点，作∠DEF＝60°交AC于点F ，若AE＝ $\sqrt{3}$ ，则AF的长是．

查看试题解析
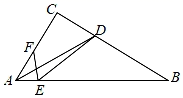26. 如图，在Rt△ABC中，AC＝4，∠BAC＝90°，∠B＝30°，D是BC上一点，AE⊥AD ， ∠ADE＝30°，连接CE ．

(1)、求证：△ADE∽△ABC；

(2)、求证：△ACE∽△ABD；

(3)、设CE＝x ，当CD＝2CE时，求x的值．

查看试题解析
27. 如图1，在矩形ABCO中，OA＝8，OC＝6，D ， E分别是AB ， BC上一点，AD＝2，CE＝3，OE与CD相交于点F ．

(1)、求证：OE⊥CD；

(2)、如图2，点G是CD的中点，延长OG交BC于H ，求CH的长．

查看试题解析
28. 如图1，在△ABC中，∠B＝∠ACB＝45°，AB＝3 $\sqrt{2}$ ，点D是BC上一点，作DE⊥AD交射线AC于E ， DF平分∠ADE交AC于F ．

(1)、求证：AB•CF＝BD•CD；

(2)、如图2，当∠AED＝75°时，求CF的长；

(3)、若CD＝2BD ，求 $\frac{A F}{E F}$ ．

查看试题解析

体温（单位：℃）	36.2	36.3	36.5	36.7	36.8
人数	8	10	7	13	12