湖南省长沙市明德教育集团初中联盟2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-23 类型:期末考试
一、单选题
-
1. 下列方程中,关于 的一元二次方程是( )A、 B、 C、 D、2. 一次函数y=2x﹣1的图象大致是( )A、
 B、
B、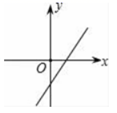 C、
C、 D、
D、 3. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 甲、乙两同学近期5次百米跑测试成绩的平均数相同,甲同学成绩的方差 =4,乙同学成绩的方差 =3.1,则对他们测试成绩的稳定性判断正确的是( )A、乙的成绩较稳定 B、甲的成绩较稳定 C、甲、乙成绩的稳定性相同 D、甲、乙成绩的稳定性无法比较5. 抛物线 是由抛物线 经过怎样的平移得到的( )A、先向右平移1个单位,再向上平移 个单位 B、先向左平移1个单位,再向下平移 个单位 C、先向右平移1个单位,再向下平移 个单位 D、先向左平移1个单位,再向上平移 个单位6. 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
3. 抛物线 的顶点坐标是( )A、 B、 C、 D、4. 甲、乙两同学近期5次百米跑测试成绩的平均数相同,甲同学成绩的方差 =4,乙同学成绩的方差 =3.1,则对他们测试成绩的稳定性判断正确的是( )A、乙的成绩较稳定 B、甲的成绩较稳定 C、甲、乙成绩的稳定性相同 D、甲、乙成绩的稳定性无法比较5. 抛物线 是由抛物线 经过怎样的平移得到的( )A、先向右平移1个单位,再向上平移 个单位 B、先向左平移1个单位,再向下平移 个单位 C、先向右平移1个单位,再向下平移 个单位 D、先向左平移1个单位,再向上平移 个单位6. 已知抛物线y=x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )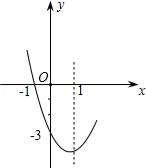 A、﹣1<x<4 B、﹣1<x<3 C、x<﹣1或x>4 D、x<﹣1或x>37. 在四边形 中, 与 相交于点 ,且 ,给出下列条件:① ;② ;③ ;④ .从中选1个作为条件,能使四边形 为平行四边形的选法有( )A、 种 B、 种 C、 种 D、 种8. 如图,▱ABCD的对角线 、 相交于点 , 是 中点,且 ,则▱ABCD的周长为( )
A、﹣1<x<4 B、﹣1<x<3 C、x<﹣1或x>4 D、x<﹣1或x>37. 在四边形 中, 与 相交于点 ,且 ,给出下列条件:① ;② ;③ ;④ .从中选1个作为条件,能使四边形 为平行四边形的选法有( )A、 种 B、 种 C、 种 D、 种8. 如图,▱ABCD的对角线 、 相交于点 , 是 中点,且 ,则▱ABCD的周长为( ) A、 B、 C、 D、9. 如图,已知矩形 沿着直线 折叠,使点C落在C′处, 交 于点E, , ,则 的长为( )
A、 B、 C、 D、9. 如图,已知矩形 沿着直线 折叠,使点C落在C′处, 交 于点E, , ,则 的长为( ) A、3 B、4 C、5 D、610. 某件羊毛衫的售价为 元,因换季促销,商家决定降价销售,在连续两次降价 后,售价降为 元,则 为( )A、 B、 C、 D、11. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、12. 已知二次函数 经过点 和点 ,交 轴于 , 两点,交 轴于 ,则:① ;②无论 取何值,此二次函数图象与 轴必有两个交点,函数图象截 轴所得的线段长度必大于 ;③当函数在 时, 随 的增大而增大;④若 ,则 .以上说法正确的有( )A、1个 B、2个 C、3个 D、4个
A、3 B、4 C、5 D、610. 某件羊毛衫的售价为 元,因换季促销,商家决定降价销售,在连续两次降价 后,售价降为 元,则 为( )A、 B、 C、 D、11. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、12. 已知二次函数 经过点 和点 ,交 轴于 , 两点,交 轴于 ,则:① ;②无论 取何值,此二次函数图象与 轴必有两个交点,函数图象截 轴所得的线段长度必大于 ;③当函数在 时, 随 的增大而增大;④若 ,则 .以上说法正确的有( )A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 已知一组数据: , ,1, , , ,这组数据的众数是 .14. 已知a,b是方程 的两根,则 的值是 .15. 如图,将平行四边形 放置在平面直角坐标系 中, 为坐标原点,若点 的坐标是 ,点 的坐标是 ,则点 的坐标是 .
 16. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x > k1x+b的解集为
16. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x > k1x+b的解集为 17. 已知A(﹣2,y1)、B(﹣3,y2)是抛物线y=(x﹣1)2+c上两点,则y1y2 . (填“>”、“=”或“<”)18. 如图,正方形 边长为 ,点 在 边上, 交 于点 , ,则 的长度是 .
17. 已知A(﹣2,y1)、B(﹣3,y2)是抛物线y=(x﹣1)2+c上两点,则y1y2 . (填“>”、“=”或“<”)18. 如图,正方形 边长为 ,点 在 边上, 交 于点 , ,则 的长度是 .
三、解答题
-
19. 解方程: .20. 在直角坐标系中,一条直线经过 , , 三点.(1)、求a的值.(2)、设这条直线与 轴相交于点 ,求 的面积.21. 为宣传6月6日世界海洋日,某校九年级举行了主题为“珍惜海洋资源,保护海洋生物多样性”的知识竞赛活动.为了解全年级500名学生此次竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并绘制出如下不完整的统计表和统计图(如图).请根据图表信息解答以下问题:
知识竞赛成绩分组统计表
组别
分数/分
频数
A
60≤x<70
a
B
70≤x<80
10
C
80≤x<90
14
D
90≤x≤100
18
 (1)、本次调查一共随机抽取了名参赛学生的成绩;(2)、表1中a=;(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有人.22. 如图,已知抛物线 经过 , 两点.
(1)、本次调查一共随机抽取了名参赛学生的成绩;(2)、表1中a=;(3)、所抽取的参赛学生的成绩的中位数落在的“组别”是;(4)、请你估计,该校九年级竞赛成绩达到80分以上(含80分)的学生约有人.22. 如图,已知抛物线 经过 , 两点.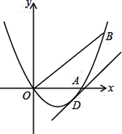 (1)、求抛物线的解析式;(2)、将直线 向下平移 个单位长度后,得到的直线与抛物线只有一个公共点 ,求 的值.23. 如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE.
(1)、求抛物线的解析式;(2)、将直线 向下平移 个单位长度后,得到的直线与抛物线只有一个公共点 ,求 的值.23. 如图,已知在△ADE中,∠ADE=90°,点B是AE的中点,过点D作DC∥AE,DC=AB,连结BD、CE. (1)、求证:四边形BDCE是菱形;(2)、若AD=8,BD=6,求菱形BDCE的面积.24. 四川是闻名天下的“熊猫之乡”,每年到大熊猫基地游玩的游客络绎不绝,大学生小张加入创业项目,项目帮助她在基地附近租店卖创意熊猫纪念品.已知某款熊猫纪念物成本为30元/件,当售价为45元/件时,每天销售250件,售价每上涨1元,销量下降10件.(1)、求每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、若每天该熊猫纪念物的销售量不低于240件的情况下,当销售单价为多少元时,每天获取的利润最大?最大利润是多少?(3)、小张决定从这款纪念品每天的销售利润中捐出150元给希望工程,为了保证捐款后这款纪念品每天剩余利润不低于3600元,试确定该熊猫纪念物销售单价的范围.25. 类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“邻好四边形”.(1)、概念理解:
(1)、求证:四边形BDCE是菱形;(2)、若AD=8,BD=6,求菱形BDCE的面积.24. 四川是闻名天下的“熊猫之乡”,每年到大熊猫基地游玩的游客络绎不绝,大学生小张加入创业项目,项目帮助她在基地附近租店卖创意熊猫纪念品.已知某款熊猫纪念物成本为30元/件,当售价为45元/件时,每天销售250件,售价每上涨1元,销量下降10件.(1)、求每天的销售量y(件)与销售单价x(元)之间的函数关系式;(2)、若每天该熊猫纪念物的销售量不低于240件的情况下,当销售单价为多少元时,每天获取的利润最大?最大利润是多少?(3)、小张决定从这款纪念品每天的销售利润中捐出150元给希望工程,为了保证捐款后这款纪念品每天剩余利润不低于3600元,试确定该熊猫纪念物销售单价的范围.25. 类比等腰三角形的定义,我们定义:有一组邻边相等的凸四边形叫做“邻好四边形”.(1)、概念理解:如图1,在四边形 中,添加一个条件,使得四边形 是“邻好四边形”,请写出你添加的一个条件;
 (2)、概念延伸:
(2)、概念延伸:下列说法正确的是 . (填入相应的序号)
①对角线互相平分的“邻好四边形”是菱形;
②一组对边平行,另一组对边相等的“邻好四边形”是菱形;
③有两个内角为直角的“邻好四边形”是正方形;
④一组对边平行,另一组对边相等且有一个内角是直角的“邻好四边形”是正方形;
(3)、问题探究:如图 ,小红画了一个 ,其中 , , ,并将 沿 的平分线 方向平移得到 ,连结 , ,要使平移后的四边形 是“邻好四边形”应平移多少距离(即线段 的长)?
26. 如图,在平面直角坐标系中,二次函数 的图象的顶点为点 ,与 轴交于点 ,与 轴交于 , 两点.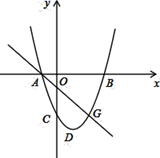 (1)、求这个二次函数的解析式;(2)、若点 是 轴上一动点,当 的周长最小时,求点 的坐标;(3)、如图,若点 是该抛物线上一点, 是直线 下方抛物线上的一动点,点 到直线 的距离为 ,求 的最大值.
(1)、求这个二次函数的解析式;(2)、若点 是 轴上一动点,当 的周长最小时,求点 的坐标;(3)、如图,若点 是该抛物线上一点, 是直线 下方抛物线上的一动点,点 到直线 的距离为 ,求 的最大值.