湖南省醴陵市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-23 类型:期末考试
一、单选题
-
1. 下列几组数中,能作为直角三角形三边长度的是( )A、6,9,10 B、5,12,17 C、4,5,6 D、1, ,2. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列一次函数中,y随x值的增大而减小的是( )A、y=3﹣2x B、y=3x+1 C、y= x+6 D、y=( ﹣2)x4. 醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91--100分的为优秀,则优秀的频率是( )
3. 下列一次函数中,y随x值的增大而减小的是( )A、y=3﹣2x B、y=3x+1 C、y= x+6 D、y=( ﹣2)x4. 醴陵市“师生诗词大赛”成绩结果统计如表,成绩在91--100分的为优秀,则优秀的频率是( )分数段
61—70
71--80
81--90
91--100
人数(人)
2
8
6
4
A、0.2 B、0.25 C、0.3 D、0.355. 点M在x轴上方,y轴左侧,距离x轴1个单位长度,距离y轴4个单位长度,则点M的坐标为( )A、(1,4) B、(﹣1,﹣4) C、(4,﹣1) D、(﹣4,1)6. 如图,▱ABCD的对角线AC、BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO的周长是( ) A、18 B、10 C、9 D、87. 四边形ABCD的对角线AC与BD相等且互相垂直,则顺次连接这个四边形四边的中点得到四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,Rt△ABC中,AB=9,BC=6,∠B=90˚,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
A、18 B、10 C、9 D、87. 四边形ABCD的对角线AC与BD相等且互相垂直,则顺次连接这个四边形四边的中点得到四边形是( )A、平行四边形 B、矩形 C、菱形 D、正方形8. 如图,Rt△ABC中,AB=9,BC=6,∠B=90˚,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )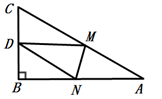 A、6 B、5 C、4 D、39. 如图,在 ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,添加一个条件,仍无法判断四边形BFDE为菱形的是( )
A、6 B、5 C、4 D、39. 如图,在 ABCD中,DE,BF分别是∠ADC和∠ABC的平分线,添加一个条件,仍无法判断四边形BFDE为菱形的是( ) A、∠A=60˚ B、DE=DF C、EF⊥BD D、BD 是∠EDF的平分线10. 如图,正方形 的边长为4,点 是 的中点,点 从点 出发,沿 移动至终点 ,设 点经过的路径长为x, 的面积为y,则下列图象能大致反映y与x函数关系的是( )
A、∠A=60˚ B、DE=DF C、EF⊥BD D、BD 是∠EDF的平分线10. 如图,正方形 的边长为4,点 是 的中点,点 从点 出发,沿 移动至终点 ,设 点经过的路径长为x, 的面积为y,则下列图象能大致反映y与x函数关系的是( ) A、
A、 B、
B、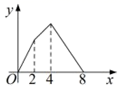 C、
C、 D、
D、
二、填空题
-
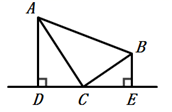
11. 如果多边形的每个外角都是45°,那么这个多边形的边数是 .12. 已知一个直角三角形的两条直角边的长分别为6cm、8cm,则它的斜边的中线长cm.13. 已知点A(m,n),B(5,3)关于x轴对称,则m + n = .14. 已知一组数据有40个,把它分成五组,第一组、第二组、第四组、第五组的频数分别是10,8,7,6,第三组频数是 .15. 将正比例函数y=3x的图象向下平移11个单位长度后,所得函数图象的解析式为 .16. 如图,在△ABC中,AD⊥DE,BE⊥DE,AC、BC分别平分∠BAD和∠ABE.点C在线段DE上.若AD=5,BE=2,则AB的长是 .
 17. 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠BOE的大小为 .
17. 如图,在矩形ABCD中,对角线AC与BD相交于点O,∠AOB=60°,AE平分∠BAD,AE交BC于E,则∠BOE的大小为 . 18. 如图,把正方形AOBC 放在直角坐标系内,对角线AB、OC相交于点D.点C的坐标是(-4,4),将正方形AOBC沿x轴向右平移,当点D落在直线y=-2x+4上时,线段AD扫过的面积为 .
18. 如图,把正方形AOBC 放在直角坐标系内,对角线AB、OC相交于点D.点C的坐标是(-4,4),将正方形AOBC沿x轴向右平移,当点D落在直线y=-2x+4上时,线段AD扫过的面积为 .
三、解答题
-
19. 如图,已知BE∥DF,∠ADF=∠CBE,AF=CE,求证:四边形DEBF是平行四边形.
 20. 如图,在平面直角坐标系xOy中,A(1,1),B(4,1),C(2,3).
20. 如图,在平面直角坐标系xOy中,A(1,1),B(4,1),C(2,3).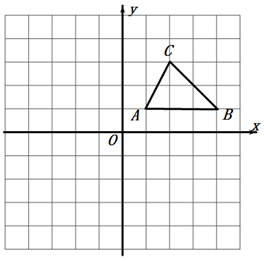 (1)、在图中作出△ABC关于y轴的轴对称图形△A′B′C′;(2)、在图中作出△ABC关于原点O中心对称图形△A"B"C".21. 如图,菱形ABCD的对角线AC、BD相交于点O,AB=10cm,OA=8cm.
(1)、在图中作出△ABC关于y轴的轴对称图形△A′B′C′;(2)、在图中作出△ABC关于原点O中心对称图形△A"B"C".21. 如图,菱形ABCD的对角线AC、BD相交于点O,AB=10cm,OA=8cm. (1)、求菱形ABCD的面积;(2)、若把△OBC绕BC的中点E旋转180˚得到四边形OBFC,求证:四边形OBFC是矩形.22. 如图,直线 交x轴于点A,y轴于点B.
(1)、求菱形ABCD的面积;(2)、若把△OBC绕BC的中点E旋转180˚得到四边形OBFC,求证:四边形OBFC是矩形.22. 如图,直线 交x轴于点A,y轴于点B. (1)、求线段AB的长和∠ABO的度数;(2)、过点A作直线L交y轴负半轴于点C,且△ABC的面积为 ,求直线L的解析式.23. 八年级(3)班同学为了解2020年某小区家庭1月份天然气使用情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
(1)、求线段AB的长和∠ABO的度数;(2)、过点A作直线L交y轴负半轴于点C,且△ABC的面积为 ,求直线L的解析式.23. 八年级(3)班同学为了解2020年某小区家庭1月份天然气使用情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:月均用气量x( )
频数(户)
频率
0<x≤10
4
0.08
10<x≤20
a
0.12
20<x≤30
16
0.32
30<x≤40
12
b
40<x≤50
10
0.20
50<x≤60
2
0.04
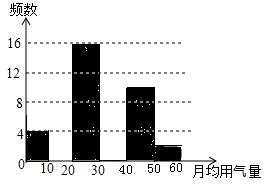 (1)、求出a,b的值,并把频数分布直方图补充完整;(2)、求月均用气量不超过30 的家庭数占被调查家庭总数的百分比;(3)、若该小区有600户家庭,根据调查数据估计,该小区月均用气量超过40 的家庭大约有多少户?24. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且CE=CF.
(1)、求出a,b的值,并把频数分布直方图补充完整;(2)、求月均用气量不超过30 的家庭数占被调查家庭总数的百分比;(3)、若该小区有600户家庭,根据调查数据估计,该小区月均用气量超过40 的家庭大约有多少户?24. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且CE=CF.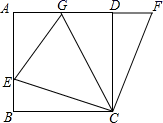 (1)、求证:BE=DF;(2)、若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?25. 甲、乙两车间同时开始加工—批服装.从开始加工到加工完这批服装甲车间工作了 小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为 (件).甲车间加工的时间为 (时), 与 之间的函数图象如图所示.
(1)、求证:BE=DF;(2)、若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?25. 甲、乙两车间同时开始加工—批服装.从开始加工到加工完这批服装甲车间工作了 小时,乙车间在中途停工一段时间维修设备,然后按停工前的工作效率继续加工,直到与甲车间同时完成这批服装的加工任务为止.设甲、乙两车间各自加工服装的数量为 (件).甲车间加工的时间为 (时), 与 之间的函数图象如图所示. (1)、甲车间每小时加工服装件数为件;这批服装的总件数为件;(2)、求乙车间维修设备后,乙车间加工服装数量 与 之间的函数关系式;(3)、求甲、乙两车间共同加工完1140件服装时甲车间所用的时间.26. 如图,在矩形ABCD中,AC=60 cm , ∠BAC=60°,点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,同时点F从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点E , F运动的时间是t秒(0<t≤15).过点F作OF⊥BC于点O , 连接OE , EF.
(1)、甲车间每小时加工服装件数为件;这批服装的总件数为件;(2)、求乙车间维修设备后,乙车间加工服装数量 与 之间的函数关系式;(3)、求甲、乙两车间共同加工完1140件服装时甲车间所用的时间.26. 如图,在矩形ABCD中,AC=60 cm , ∠BAC=60°,点E从点A出发沿AB方向以2 cm/秒的速度向点B匀速运动,同时点F从点C出发沿CA方向以4 cm/秒的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点E , F运动的时间是t秒(0<t≤15).过点F作OF⊥BC于点O , 连接OE , EF. (1)、求证:AE=OF;(2)、四边形AEOF能够成为菱形吗?如果能,求出相应的t值,如果不能,请说明理由;(3)、当t为何值时,△OEF为直角三角形?请说明理由.
(1)、求证:AE=OF;(2)、四边形AEOF能够成为菱形吗?如果能,求出相应的t值,如果不能,请说明理由;(3)、当t为何值时,△OEF为直角三角形?请说明理由.