广西壮族自治区南宁市马山县2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2020-09-23 类型：期中考试

进入出卷网下载

一、选择题

1. $- \frac{1}{2019}$ 的倒数是（）

A、-2019 B、2019 C、 $\frac{1}{2019}$ D、 $- \frac{1}{2019}$

查看试题解析
2. 在8.5，﹣π，3.14， $\frac{22}{7}$ ，0， $- \frac{1}{3}$ 各数中，正有理数的个数有（）

A、3 B、4 C、5 D、6

查看试题解析
3. 计算 $3 - (- 3)$ 的结果是（）

A、6 B、3 C、0 D、－6

查看试题解析
4. （﹣2）³的值是（）

A、﹣5 B、﹣6 C、﹣8 D、﹣9

查看试题解析
5. 有理数a、b在数轴上的表示如图所示，那么（）

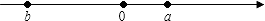A、﹣b＞a B、﹣a＜b C、b＞a D、|a|＞|b|

查看试题解析
6. 下列去括号错误的是（）

A、2x²﹣（x﹣3y）=2x²﹣x+3y B、 $\frac{1}{3}$ x²+（3y²﹣2xy）= $\frac{1}{3}$ x²﹣3y²+2xy C、a²+（﹣a+1）=a²﹣a+1 D、﹣（b﹣2a）﹣（﹣a²+b²）=﹣b+2a+a²﹣b²

查看试题解析
7. 在①2x²﹣3xy﹣1是二次三项式；②近似数2.5万精确到十分位；③ $- \frac{2}{3} π x y^{2}$ 的系数是 $- \frac{2}{3} π$ ；④﹣2²ab²的次数是6，错误的个数有（）

A、4 B、3 C、2 D、1

查看试题解析
8. 在下列各式中，计算正确的是（）

A、 $- 12 x + 7 x = - 5 x$ B、 $5 y^{2} - 7 y^{2} = 2$ C、 $3 a + 2 b = 5 a b$ D、 $4 m^{2} n - 2 m n^{2} = 2 m n$

查看试题解析
9. 单项式2a^xb²与﹣a³b^y是同类项，则x^y等于（）

A、﹣6 B、6 C、﹣9 D、9

查看试题解析
10. 已知 $x - 2 y = - 2$ ，则 $3 + 2 x - 4 y$ 的值是（）.

A、0 B、-1 C、3 D、5

查看试题解析
11. a、b互为倒数，x、y互为相反数且y $\neq 0$ ，那么代数式 (a+b)(x+y)－ab－ $\frac{x}{y}$ 的值为（）

A、2 B、1 C、－1 D、0

查看试题解析
12. 若ab≠0，则 $\frac{a}{|a|}$ + $\frac{|b|}{b}$ 的值不可能是（　　）

A、2 B、0 C、-2 D、1

查看试题解析

二、填空题

13. 如果＋3吨表示运入仓库的大米吨数，那么运出5吨大米表示为.

查看试题解析
14. 比较大小： $- \frac{1}{2}$ $- \frac{3}{4}$ .

查看试题解析
15. 在网络上搜索“奔跑吧,兄弟”,能搜索到与之相关的结果为35 800 000个,将35 800 000用科学记数法表示为 .

查看试题解析
16. 根据如右图所示的程序计算，若输入x的值为1，则输出y的值为.

查看试题解析
17. 现定义某种运算“*”，对给定的两个有理数a、b（a≠0），有a*b=a﹣a^b ，则（﹣3）*2=.

查看试题解析
18. 观察一列数： $\frac{1}{2} ， - \frac{2}{5} ， \frac{3}{10} ， - \frac{4}{17} ， \frac{5}{26} ， - \frac{6}{37}$ 根据规律，请你写出第12个数是.

查看试题解析

三、解答题

19. 在数轴上表示下列各数：0，－4，2 $\frac{1}{2}$ ，－2，|－5|，－(－1)，并用“＜”号连接.

查看试题解析
20. 计算题：

(1)、﹣3﹣（﹣10）+（﹣9）﹣10

(2)、（﹣1）÷（ $- \frac{3}{4}$ ） $\times \frac{1}{4}$

(3)、（ $- \frac{1}{6} + \frac{3}{4} - \frac{1}{12}) \div (- \frac{1}{48})$

(4)、﹣1⁴﹣（1﹣9）÷|﹣4|×[3﹣（﹣3）²]

查看试题解析
21. 化简：

(1)、2（2a﹣3b）+3（2b﹣3a）

(2)、4x²﹣（2x²+x﹣1）+（2﹣x²+3x）

查看试题解析
22. 先化简，再求值： $- (a^{2} + 2 a) + 3 (a^{2} - 3 a- \frac{1}{3})$ ，其中a=﹣2．

查看试题解析
23. 如图所示：

(1)、用代数式表示阴影部分的面积；

(2)、当a=10，b=4时，π取值为3.14，求阴影部分的面积．

查看试题解析
24. 为体现社会对老师的尊重，教师节这一天上午，出租车司机小王在东西向的公路上免费接送老师，如果规定向东为正，向西为负，出租车的行程如下（单位：千米）：+5，﹣4，+3，﹣10，+3，﹣9．

(1)、最后一名老师送到目的时，小王距出租车出发点的距离是多少千米；

(2)、若汽车耗油量为0.4升/千米，则这天上午小王的汽车共耗油多少升？

查看试题解析
25. 某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月上班人数不一定相等，实每月生产量与计划量相比情况如下表（增加为正，减少为负）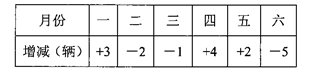

(1)、生产量最多的一天比生产量最少的一天多生产多少辆？

(2)、半年内总生产量是多少？比计划多了还是少了，增加或减少多少？

查看试题解析
26. 服装厂生产一种夹克和 T 恤，夹克每件定价 200 元，T 恤每件定价 60 元，厂方在开展促销活动期间，向客户提供两种优惠方案：
①买一件夹克送一件T 恤；

②夹克和T 恤都按定价的80%付款，现某客户要到该服装厂购买夹克30件，T 恤x件，（x＞30）.

(1)、若该客户按方案①购买，夹克需付款元，T 恤需付款元，（用含 x 的式子表示）
若该客户按方案②购买，夹克需付款元，T 恤需付款元，（用含x 的式子表示）

(2)、按方案①购买夹克和 T 恤共需付款元，（用含 x 的式子表示）按方案②购买夹克和T 恤共需付款元，（用含 x 的式子表示）

(3)、若两种优惠方案可同时使用，当 x=40 时，你能给出一种更为省钱的购买方案吗？试写出你的购买方案，并说明理由.

查看试题解析