初中数学人教版九年级上学期 第二十四章 24.2 点和圆、直线和圆的位置关系
试卷更新日期:2020-09-22 类型:同步测试
一、单选题
-
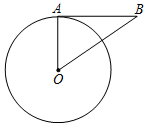
1. 一个点到圆的最大距离为11,最小距离为5,则圆的半径为( ).A、16或6 B、3或8 C、3 D、82. 已知⊙O的半径为10cm,OP=8cm,则点P和⊙O的位置关系是( )A、点P在圆内 B、点P在圆上 C、点P在圆外 D、无法判断3. 若点B(a,0)在以A(1,0)为圆心,2为半径的圆内,则a的取值范围为( )A、a<-1 B、a>3 C、-1 <a < 3 D、a≥-1且4. 已知⊙O的半径为5,点 的坐标为(-1,0),点 的坐标为(-3,4),则点 与⊙O的位置关系是( )A、点P在⊙O的外 B、点P在⊙O的上 C、点P在⊙O的内 D、不能确定5. 如图,AB是⊙O的切线,A为切点,连接OA,OB.若∠B=35°,则∠AOB的度数为( )
 A、65° B、55° C、45° D、35°6. 如图所示, 、 分别与 相切于A、B两点,点C为 上一点,连接 、 ,若 ,则 的度数为( )
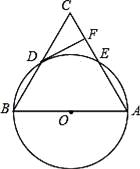
A、65° B、55° C、45° D、35°6. 如图所示, 、 分别与 相切于A、B两点,点C为 上一点,连接 、 ,若 ,则 的度数为( )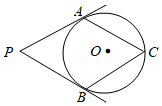 A、 B、 C、 D、7. 如图,AB和AC与圆O分别相切于点B和点C,点D是圆O上一点,若∠BAC=74°,则∠BDC等于( )
A、 B、 C、 D、7. 如图,AB和AC与圆O分别相切于点B和点C,点D是圆O上一点,若∠BAC=74°,则∠BDC等于( ) A、46° B、53° C、74° D、106°8. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )
A、46° B、53° C、74° D、106°8. 如图, 内接于圆, ,过点C的切线交 的延长线于点 .则 ( )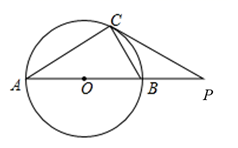 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 用反证法证明“三角形的三个内角中,至少有一个大于或等于60°”时,应先假设10. 已知⊙O的面积为36π,若PO=7,则点P在⊙O .11. 两直角边长分别为6和8的直角三角形的外接圆直径是 .
12. AB是⊙O的直径,PA切⊙O于点A , PO交⊙O于点C;连接BC , 若∠P=40°,则∠B等于 .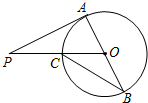 13. 如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,且∠BAC=50°,则∠ACD=°.
13. 如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,且∠BAC=50°,则∠ACD=°. 14. 已知在Rt△ABC中,∠C=90º,AC=3,BC=4,⊙C与斜边AB相切,那么⊙C的半径为.15. 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆∁n的半径分别是r1、r2、r3…、rn , 则 =.
14. 已知在Rt△ABC中,∠C=90º,AC=3,BC=4,⊙C与斜边AB相切,那么⊙C的半径为.15. 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆∁n的半径分别是r1、r2、r3…、rn , 则 =.
三、解答题
-
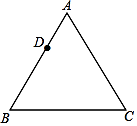
16. 如图,在△ABC中,AB=AC,P是△ABC内的一点,且∠APB>∠APC,求证:PB<PC(反证法)
 17. 如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC.BC平分∠ABD.
17. 如图所示,AB是⊙O的直径,点C为⊙O上一点,过点B作BD⊥CD,垂足为点D,连结BC.BC平分∠ABD.求证:CD为⊙O的切线.