陕西省西安市经开区2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-09-22 类型:期中考试
一、选择题
-
1. 下列关于x的方程中,一定是一元二次方程的为( )A、ax2+bx+c=0 B、x2﹣2=(x+3)2 C、x2+ ﹣5=0 D、x2=02. 将一个正方体沿正面相邻两条棱的中点连线截去一个三棱柱,得到一个如图所示的几何体,则该几何体的左视图是( )
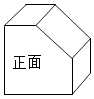 A、
A、 B、
B、 C、
C、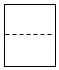 D、
D、 3. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、4. 如图,直线 l1 ∥l2 ∥l3 ,直线 AC 分别交 l1 , l2 , l3 于点 A,B,C;直线 DF 分别交 l1 , l2 , l3 于点 D,E,F,AC 与 DF 相交于点 G,且 AG=2,GB=1,BC=5,则 的值是( )
3. 关于 的一元二次方程 有实数根,则 的取值范围是 ( )A、 B、 C、 D、4. 如图,直线 l1 ∥l2 ∥l3 ,直线 AC 分别交 l1 , l2 , l3 于点 A,B,C;直线 DF 分别交 l1 , l2 , l3 于点 D,E,F,AC 与 DF 相交于点 G,且 AG=2,GB=1,BC=5,则 的值是( )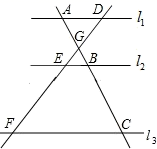 A、 B、2 C、 D、5. 若x=-2 是关于x的一元二次方程x2- ax+a2=0的一个根,则a的值为( )
A、 B、2 C、 D、5. 若x=-2 是关于x的一元二次方程x2- ax+a2=0的一个根,则a的值为( )
A、1或4 B、-1或-4 C、-1或4 D、1或-46. 如图,已知△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC相交于点F,图中相似的三角形有( )对. A、3 B、4 C、5 D、67.
A、3 B、4 C、5 D、67.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,则四边形ABCD只需要满足一个条件,是( )
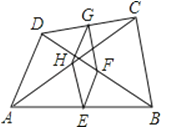 A、四边形ABCD是梯形 B、四边形ABCD是菱形 C、对角线AC=BD D、AD=BC8. 如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若 , ,则△ACD的面积为( )
A、四边形ABCD是梯形 B、四边形ABCD是菱形 C、对角线AC=BD D、AD=BC8. 如图,在△ABC中,D,E分别是AB,BC边上的点,且DE∥AC,若 , ,则△ACD的面积为( )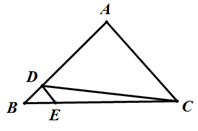 A、64 B、72 C、80 D、969. 如图,已知正方形ABCD的边长为5,点E,F分别在BC和CD边上,分别连接AE、AF、EF,若∠EAF=45°,则△CEF的周长是( )
A、64 B、72 C、80 D、969. 如图,已知正方形ABCD的边长为5,点E,F分别在BC和CD边上,分别连接AE、AF、EF,若∠EAF=45°,则△CEF的周长是( )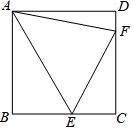 A、6+2 B、8.5 C、10 D、1210. 如图在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;② ;③△PMN为等边三角形;④当∠ABC=45°时,BN= BC,其中正确的是( )
A、6+2 B、8.5 C、10 D、1210. 如图在△ABC中∠A=60°,BM⊥AC于点M,CN⊥AC于点N,P为BC边的中点,连接PM,PN,则下列结论:①PM=PN;② ;③△PMN为等边三角形;④当∠ABC=45°时,BN= BC,其中正确的是( )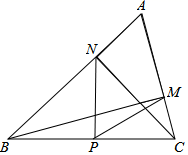 A、①②③ B、①②④ C、①③④ D、②③④
A、①②③ B、①②④ C、①③④ D、②③④二、填空题
-
11. 如果3x=2y(x,y均不为0),那么x:y=.12. 在“阳光体育”活动时间,张海亮、张红武、李优、王安进行一次羽毛球单打比赛,要从中选出两位同学打第一次比赛,则恰好选中李优、王安两位同学的概率是.13. 电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体.如图:若舞台AB长为20m,试计算主持人应走到离A点至少m处.(结果精确到0.1m)
 14. 为了估计池塘里有多少条鱼,从池塘里捕捉了100条鱼,做上标记, 然后放回池塘里,经过一段时间后,等有标记的鱼完全混合于池塘中鱼群后, 再捕第二次样本鱼200条,发现其中有标志的鱼25条,你估计一下,该池塘里现在有鱼条.15. 如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2 , 设小道进出口的宽度为x m,根据条件,可列出方程: .
14. 为了估计池塘里有多少条鱼,从池塘里捕捉了100条鱼,做上标记, 然后放回池塘里,经过一段时间后,等有标记的鱼完全混合于池塘中鱼群后, 再捕第二次样本鱼200条,发现其中有标志的鱼25条,你估计一下,该池塘里现在有鱼条.15. 如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2 , 设小道进出口的宽度为x m,根据条件,可列出方程: . 16. 如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为.
16. 如图,在矩形ABCD中,AB=3,AD=4,连接AC,O是AC的中点,M是AD上一点,且MD=1,P是BC上一动点,则PM﹣PO的最大值为.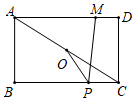
三、解答题
-
17. 解下列方程(1)、x(x﹣5)=14(2)、3x(x﹣1)=2﹣2x18. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,1),B(-1,4),C(-3,2).
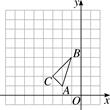 (1)、以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1 , 并直接写出C1点的坐标;(2)、如果点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.19. 已知关于x的一元二次方程方程x2﹣2mx+m2﹣m﹣1=0有两个实数根.(1)、求m的取值范围.(2)、若该方程的两个实数根x1 , x2满足x1+x2=1﹣x1x2 , 求m的值.20. “五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.(1)、顾客甲购物1000元,则他最少可获元代金券,最多可获元代金券.(2)、请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率.21. 如图,在 中, 的平分线 分别与 、 交于点 、 .
(1)、以原点O为位似中心,位似比为1∶2,在y轴的左侧,画出△ABC放大后的图形△A1B1C1 , 并直接写出C1点的坐标;(2)、如果点D(a,b)在线段AB上,请直接写出经过(1)的变化后点D的对应点D1的坐标.19. 已知关于x的一元二次方程方程x2﹣2mx+m2﹣m﹣1=0有两个实数根.(1)、求m的取值范围.(2)、若该方程的两个实数根x1 , x2满足x1+x2=1﹣x1x2 , 求m的值.20. “五一”小长假期间,某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性购物满500元以上均可获得两次摸球的机会(摸出小球后放回).超市根据两小球所标金额的和返还相应的代金券.(1)、顾客甲购物1000元,则他最少可获元代金券,最多可获元代金券.(2)、请用树形图或列表方法,求出顾客甲获得不低于30元(含30元)代金券的概率.21. 如图,在 中, 的平分线 分别与 、 交于点 、 .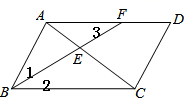 (1)、求证: ;(2)、当 时,求 的值.22. 如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.
(1)、求证: ;(2)、当 时,求 的值.22. 如图是位于陕西省西安市荐福寺内的小雁塔,是中国早期方形密檐式砖塔的典型作品,并作为丝绸之路的一处重要遗址点,被列入《世界遗产名录》.小铭、小希等几位同学想利用一些测量工具和所学的几何知识测量小雁塔的高度,由于观测点与小雁塔底部间的距离不易测量,因此经过研究需要进行两次测量,于是在阳光下,他们首先利用影长进行测量,方法如下:小铭在小雁塔的影子顶端D处竖直立一根木棒CD,并测得此时木棒的影长DE=2.4米;然后,小希在BD的延长线上找出一点F,使得A、C、F三点在同一直线上,并测得DF=2.5米.已知图中所有点均在同一平面内,木棒高CD=1.72米,AB⊥BF,CD⊥BF,试根据以上测量数据,求小雁塔的高度AB.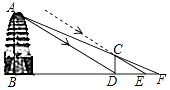 23. 如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.
23. 如图,将▱ABCD的边DC延长到点E,使CE=DC,连接AE,交BC于点F.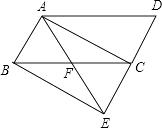 (1)、求证:△ABF≌△ECF;(2)、若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.24. 因抖音等新媒体的传播,西安已成为最著名的网红旅游城市之一,2016年“十一”黄金周期间,西安接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗6元,借鉴以往经验;若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗(1)、求出2016年至2018年十一长假期间游客人次的年平均增长率;(2)、为了维护城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天盈利6300元?25. 如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.
(1)、求证:△ABF≌△ECF;(2)、若∠AFC=2∠D,连接AC、BE,求证:四边形ABEC是矩形.24. 因抖音等新媒体的传播,西安已成为最著名的网红旅游城市之一,2016年“十一”黄金周期间,西安接待游客近1000万人次,2018年“十一”黄金周期间,接待游客已达1690万人次,古城西安美食无数,一家特色小面店希望在长假期间获得较好的收益,经测算知,该小面的成本价为每碗6元,借鉴以往经验;若每碗卖25元,平均每天将销售300碗,若价格每降低1元,则平均每天多销售30碗(1)、求出2016年至2018年十一长假期间游客人次的年平均增长率;(2)、为了维护城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天盈利6300元?25. 如图,已知一个直角三角形纸片ACB,其中∠ACB=90°,AC=4,BC=3,E、F分别是AC、AB边上点,连接EF.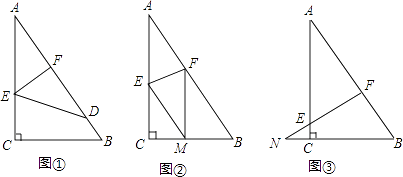 (1)、图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;(2)、如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
(1)、图①,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=3S△EDF , 求AE的长;(2)、如图②,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)、如图③,若FE的延长线与BC的延长线交于点N,CN=1,CE= ,求 的值.