陕西省汉中市城固县2020届九年级上学期数学期中考试试卷
试卷更新日期：2020-09-22 类型：期中考试
一、选择题
-
1. 下列方程中，属于一元二次方程的是（ ）A、x+2y＝1 B、ax2+bx+c＝0 C、3x+ ＝4 D、x2﹣2＝02. 下列结论中，正确的是（ ）A、四边相等的四边形是正方形 B、对角线相等的菱形是正方形 C、正方形两条对角线相等，但不互相垂直平分 D、矩形、菱形、正方形都具有“对角线相等”的性质3. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有2个，黑球有n个.随机地从袋子中摸出一个球，记录下颜色后，放回袋子中并摇匀.经过大量重复试验发现摸出白球的频率稳定在0.4附近，则n的值为（ ）A、2 B、3 C、4 D、54.
如图，菱形中，对角线AC、BD交于点O ， E为AD边中点，菱形ABCD的周长为28，则OE的长等于（ ）
A、3.5 B、4 C、7 D、145. 如果两个相似三角形对应边之比是 ，那么它们的对应中线之比是（ ）A、1:3 B、1:4 C、1:6 D、1:96. 已知关于 的方程 ，下列说法正确的是（ ）A、当 时，方程无解 B、当 时，方程有一个实数解 C、当 时，方程有两个相等的实数解 D、当 时，方程总有两个不相等的实数解7. 如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1：2，点A的坐标为(1，0)，则E点的坐标为（ ）
A、(2，0) B、(1，1) C、( ， ) D、(2，2)8. 共享单车为市民出行带来了方便，某单车公司第一个月投放1000辆单车，计划第三个月投放单车数量比第一个月多440辆.设该公司第二、三连个月投放单车数量的月平均增长率为x，则所列方程正确的是（ ）A、1000(1＋x)2＝440 B、1000(1＋x)2＝1000 C、1000(1＋2x)＝1000＋440 D、1000(1＋x)2＝1000＋4409. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，CH┴AF与点H，那么CH的长是（ ）
A、 B、 C、 D、10. 如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F，交AB于E，若点G是AE中点且∠AOG＝30°，则下列结论正确的个数为（ ）
（1）△OGE是等边三角形；（2）DC＝3OG；（3）OG＝ BC；（4）S△AOE＝ S矩形ABCD
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 线段AB长为10cm ， 点C是AB的黄金分割点，则AC的长为（结果精确到0.1cm）．12. 在数学活动课上，小派运用统计方法估计瓶子中的豆子的数量．他先取出100粒豆子，给这些豆子做上记号，然后放回瓶子中，充分摇匀之后再取出100粒豆子，发现其中8粒有刚才做的记号，利用得到的数据可以估计瓶子中豆子的数量约为 粒．13. 如图，一电线杆AB的影子分别落在了地上和墙上.同一时刻，小明竖起1米高的直杆MN，量得其影长MF为0.5米，量得电线杆AB落在地上的影子BD长3米，落在墙上的影子CD的高为2米.你能利用小明测量的数据算出电线杆AB的高吗？
14. 如图，菱形ABCD中，AB＝2，∠A＝120°，点E、F分别在边AB、AD上且AE＝DF，则△AEF面积的最大值为.
三、解答题
-
15. 解方程：3(x-5)2=2(5-x)16. 先化简：（ ）÷ ，再从2，﹣2，1，0，﹣1中选择一个合适的数进行计算.17. 已知：△ABC中，∠A＝36°，AB＝AC，用尺规求作一条过点B的直线，使得截出的一个三角形与△ABC相似.（保留作图痕迹，不写作法）
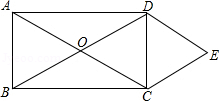
18. 已知关于x的方程 .(1)、当该方程的一个根为1时，求a的值及该方程的另一根；(2)、求证：不论a取何实数，该方程都有两个不相等的实数根.19. 如图，某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度，他们通过调整测量位置，使斜边DF与地面保持平行，并使边DE与旗杆顶点A在同一直线上，已知DE＝1米，EF＝0.5米，测点D到地面的距离DG＝3米，到旗杆的水平距离DC＝40米，求旗杆的高度.
20. 端午节放假期间，小明和小华准备到宜宾的蜀南竹海（记为A）、兴文石海（记为B）、夕佳山民居（记为C）、李庄古镇（记为D）的一个景点去游玩，他们各自在这四个景点中任选一个，每个景点都被选中的可能性相同．(1)、小明选择去蜀南竹海旅游的概率为 ．(2)、用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率．21. 如图，矩形ABCD的对角线相交于点O，DE∥AC，CE∥BD.求证：四边形OCED是菱形.
22. 某商场销售一批名牌衬衫，平均每天可以销售20件，每件盈利40元，为了扩大销售，增加利润，尽量减少库存，商场决定采取适当的降价措施，经调查发现，如果每件衬衫降价1元，商场平均每天多售出2件，若商场平均每天要盈利1200元，每件衬衫应降价多少元？23. 太原双塔寺又名永祚寺，是国家级文物保护单位，由于双塔（舍利塔、文峰塔）耸立，被人们称为“文笔双塔”，是太原的标志性建筑之一，某校社会实践小组为了测量舍利塔的高度，在地面上的C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，舍利塔的塔尖点B正好在同一直线上，测得EC＝4米，将标杆CD向后平移到点C处，这时地面上的点F，标杆的顶端点H，舍利塔的塔尖点B正好在同一直线上（点F，点G，点E，点C与塔底处的点A在同一直线上），这时测得FG＝6米，GC＝53米.请你根据以上数据，计算舍利塔的高度AB.
24. 如图，在△ABC中.AB＝AC，AD⊥BC于D，作DE⊥AC于E，F是AB中点，连EF交AD于点G.
(1)、求证：AD2＝AB•AE；(2)、若AB＝3，AE＝2，求 的值.25. 已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝ AC
(1)、求过点A，B的直线的函数表达式；(2)、在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；(3)、在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由.