陕西省宝鸡市岐山县2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-09-22 类型:期中考试
一、选择题
-
1. 下列性质中正方形具有而菱形不具有的是( )A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、每一条对角线平分一组对角2. 今年国庆假期间,小明与小亮两家准备从九龙山、金丝峡、红河谷三个景点中任选一个景点游玩。则两家选到同一个景点的概率是( )A、 B、 C、 D、3. 已知 是方程 的两个根,则 的值为( )A、2 B、-2 C、1 D、-14. 将代数式 配方成 形式为( )A、 B、 C、 D、5.
如图,由于各人的习惯不同,双手交叉时左手大拇指或右手大拇指在上是一个随机事件,曾老师对他任教的学生做了一个调查,统计结果如下表所示:
2011届
2012届
2013届
2014届
2015届
参与实验的人数
106
110
98
104
112
右手大拇指在上的人数
54
57
49
51
56
频率
0.509
0.518
0.500
0.490
0.500
根据表格中的数据,你认为在这个随机事件中,右手大拇指在上的概率可以估计为( )
 A、0.6 B、0.5 C、0.45 D、0.46. 现代互联网技术的广泛应用,促进快递行业高速发展,据调查,我市某家快递公司,今年3月份与5月份完成投递的快递总件数分别为6.3万件和8万件.设快递公司这两个月投递总件数的月平均增长率为x,则下列方程正确的是( )A、6.3(1+2x)=8 B、6.3(1+x)=8 C、6.3(1+x)2=8 D、6.3+6.3(1+x)+6.3(1+x)2=87. 如果E,F,G,H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是( )A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线相等且互相平分8. 在一个不透明的袋子里,有2个白球和2个红球,它们只有颜色上的区别,其它均相同,从袋子里随机摸出一个球记下颜色不放回,再随机地摸出一个球,则两次都摸到白球的概率为( )A、 B、 C、 D、9. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠110. 如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形 ,转动这个四边形,使它形状改变,当 , 时, 等于( )
A、0.6 B、0.5 C、0.45 D、0.46. 现代互联网技术的广泛应用,促进快递行业高速发展,据调查,我市某家快递公司,今年3月份与5月份完成投递的快递总件数分别为6.3万件和8万件.设快递公司这两个月投递总件数的月平均增长率为x,则下列方程正确的是( )A、6.3(1+2x)=8 B、6.3(1+x)=8 C、6.3(1+x)2=8 D、6.3+6.3(1+x)+6.3(1+x)2=87. 如果E,F,G,H是四边形ABCD四条边的中点,要使四边形EFGH是矩形,那么四边形ABCD应具备的条件是( )A、一组对边平行而另一组对边不平行 B、对角线相等 C、对角线互相垂直 D、对角线相等且互相平分8. 在一个不透明的袋子里,有2个白球和2个红球,它们只有颜色上的区别,其它均相同,从袋子里随机摸出一个球记下颜色不放回,再随机地摸出一个球,则两次都摸到白球的概率为( )A、 B、 C、 D、9. 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )A、k> B、k≥ C、k> 且k≠1 D、k≥ 且k≠110. 如图,将四根长度相等的细木条首尾相连,用钉子钉成四边形 ,转动这个四边形,使它形状改变,当 , 时, 等于( )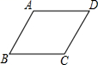 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
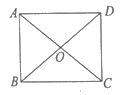
11. 小明和他的爸爸妈妈共3人站成一排拍照,他和爸爸相邻的概率是。12. 如图,矩形 的对角线 相交于点 ,请你添加一个适当的条件(只填一个即可) , 使其成为正方形。
 13. 已知关于 的一元二次方程 有一根为2,则方程的另一根为。14. 如图,点E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB= °.
13. 已知关于 的一元二次方程 有一根为2,则方程的另一根为。14. 如图,点E为正方形ABCD外一点,AE=AD,∠ADE=75°,则∠AEB= °. ,
,三、解答题
-
15. 用适当的方法解下列方程:(1)、 ;(2)、16. 尺规作图:如图,已知线段 ,求作一个菱形 ,使 为菱形 的一条对角线(不写作法,保留作图痕迹)。
 17. 先阅读材料,然后按照要求答题。
17. 先阅读材料,然后按照要求答题。阅读材料:为了解方程 ,我们可以将 视为一个整体,然后设 , ,则原方程可化为:
①
解得:
当 时, ,
∴ ,
当 时, ,
∴ ,
∴原方程的解为: ,
解答问题:
(1)、上述解题过程,在由原方程得到方程①的过程中,利用法达到了解方程的目的,体现了转化的数学思想;(2)、请利用以上知识解决问题:若 ,求 的值。18. 在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.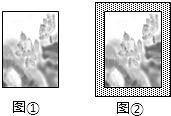 19. 四边形ABCD是平行四边形,对角线AC平分∠DAB,AC与BD相交于点O,DE⊥AB于E点.
19. 四边形ABCD是平行四边形,对角线AC平分∠DAB,AC与BD相交于点O,DE⊥AB于E点.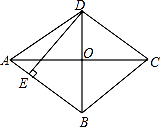 (1)、求证:四边形ABCD是菱形;(2)、若AC=8,BD=6,求DE的长度.20. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)
(1)、求证:四边形ABCD是菱形;(2)、若AC=8,BD=6,求DE的长度.20. 某超市在端午节期间开展优惠活动,凡购物者可以通过转动转盘的方式享受折扣优惠,本次活动共有两种方式,方式一:转动转盘甲,指针指向A区域时,所购买物品享受9折优惠、指针指向其它区域无优惠;方式二:同时转动转盘甲和转盘乙,若两个转盘的指针指向每个区域的字母相同,所购买物品享受8折优惠,其它情况无优惠.在每个转盘中,指针指向每个区城的可能性相同(若指针指向分界线,则重新转动转盘)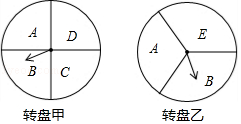 (1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.21.
(1)、若顾客选择方式一,则享受9折优惠的概率为多少;(2)、若顾客选择方式二,请用树状图或列表法列出所有可能,并求顾客享受8折优惠的概率.21.如图,将矩形纸片ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E.
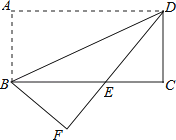 (1)、求证:△DCE≌△BFE;(2)、若CD=2,∠ADB=30°,求BE的长.
(1)、求证:△DCE≌△BFE;(2)、若CD=2,∠ADB=30°,求BE的长.