重庆市万州区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-22 类型：期末考试

进入出卷网下载

一、选择题

1. 在方程3x﹣y＝2，x+1＝0， $\frac{1}{2}$ x＝ $\frac{1}{2}$ ，x²﹣2x﹣3＝0中一元一次方程的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 在下列图形中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 若a＞b，则下列不等式正确的是（）

A、a﹣2＜b﹣2 B、 $\frac{a}{4}$ ＞ $\frac{b}{4}$ C、am＜bm D、am²＞bm²

查看试题解析
4. 下列各组线段能组成三角形的是（）

A、1、2、3 B、4、5、10 C、3、5、1 D、5、5、1

查看试题解析
5. 在下列正多边形瓷砖中，若仅用一种正多边形瓷砖铺地面，则不能将地面密铺的是（）

A、正三角形 B、正四边形 C、正六边形 D、正八边形

查看试题解析
6. 如果关于x的方程3x+2k-5=0的解为x=-3，则k的值是（）

A、2 B、-2 C、7 D、-7

查看试题解析
7. 如图， $△ A B C ≌ △ D E C$ ，A和D，B和E是对应点，B，C，D在同一直线上，且CE＝5，AC＝7，则BD的长为（）

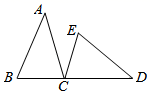A、12 B、7 C、2 D、14

查看试题解析
8. 若（m﹣3）x+4y^|2m^﹣^5|＝25是关于x，y的二元一次方程，则m的值是（）

A、3或2 B、2 C、3 D、任何数

查看试题解析
9. 按照如图所示的运算程序，若输入的x的值为4，则输出的结果是（）

A、21 B、89 C、261 D、361

查看试题解析
10. 在下列说法中，（1）角的对称轴是它的角平分线所在直线；（2）图形的平移、旋转、轴对称变换不改变图形的形状和大小；（3）三角形的三条高线一定在三角形内；（4）多边形的外角和是360°.则正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
11. 为响应习总书记“绿水青山，就是金山银山”的号召，重庆某国营企业2020年3月争取到一批植树任务，领到一批树苗，按下列方法依次由各车间领取：第一车间领取200棵和余下的 $\frac{1}{10}$ ，第二车间领取300棵和余下的 $\frac{1}{10}$ ，第三车间领取400棵和余下的 $\frac{1}{10}$ ，……，最后树苗全部被领完，且各车间领取的树苗数相等，则领到树苗的车间数和树苗总棵树分别为（）

A、7、6300 B、8、7200 C、9、8100 D、6、5400

查看试题解析
12. 已知关于x、y的方程组 ${\begin{array}{l} a x + 3 y = 12 \\ x - 3 y = 0 \end{array}$ 的解为整数，且关于x的不等式组 ${\begin{array}{l} 2 (x + 1) < x + 5 \\ 3 x > a - 4 \end{array}$ 有且仅有5个整数解，则所有满足条件的整数a的和为（）

A、﹣1 B、﹣2 C、﹣8 D、﹣6

查看试题解析

二、填空题

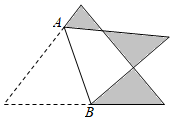
13. 列方程：“a的2倍与5的差等于a的3倍”为：.

查看试题解析
14. 一个多边形的内角和为2700°，则这个多边形的边数是边.

查看试题解析
15. 方程x+2y＝5的正整数解有个.

查看试题解析
16. 将图中的三角形纸片沿AB折叠所得的AB右边的图形的面积与原三角形面积之比为2：3，已知图中重叠部分的面积为5，则图中三个阴影部分的三角形的面积之和为.

查看试题解析
17. 如图，一副直角三角板 $△$ ABC和 $△$ DEF，∠F＝30°，将 $△$ ABC和 $△$ DEF放置如图2的位置，点B、D、C、F在同一直线上，点A在DE上， $△$ ABC固定不动，当 $△$ EDF绕点D逆时针旋转至180°的过程中（不含180°），当旋转角为时，EF与 $△$ ABC的边垂直.

查看试题解析
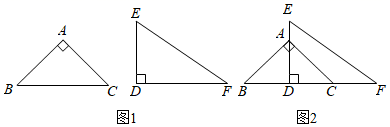18. 若定义f（x）=3x-2，如f（-2）=3×（-2）-2=-8.下列说法中：①当f（x）=1时，x=1；②对于正数x，f（x）＞f（-x）均成立；③f（x-1）+f（1-x）=0；④当且仅当a=2时，f（a-x）=a-f（x）.其中正确的是.（填序号）

查看试题解析

三、解答题

19. 解方程或不等式组并把不等式组的解集表示在数轴上.

(1)、3（x+1）+2（x﹣1）＝6；

(2)、 ${\begin{array}{l} 3 (x + 1) < 2 x + 5 \\ \frac{x - 1}{4} ⩽ \frac{x}{3} \end{array}$ .

查看试题解析
20. 如图，在由边长为1个单位长度的小正方形组成的10×10网格中，已知 $△$ ABC的顶点均为网格线的交点.

（ 1 ）将 $△$ ABC先向下平移7个单位长度，再向左平移6个单位长度得到 $△$ A₁B₁C₁ ，画出 $△$ A₁B₁C₁；

（ 2 ）画出 $△$ A₁B₁C₁关于直线l成轴对称的 $△$ A₂B₂C₂.

查看试题解析
21. 已知方程组 ${\begin{array}{l} x - y = 4 m ① \\ 2 x + y = 2 m + 3 ② \end{array}$ 的解满足x﹣2y＜8.

(1)、求m的取值范围；

(2)、当m为正整数时，求代数式2（m²﹣m+1）﹣3（m²+2m﹣5）的值.

查看试题解析
22. 5月的第二个周日是母亲节，小东为了精心设计一份手工礼物送给妈妈，为尽快完成手工礼物，小东骑自行车到位于家正西方向的商店购买材料.小东离家15分钟时自行车出现故障，小东立即打电话通知在家看报纸的父亲贺明带上工具箱来帮忙维修，同时小东以原来一半的速度推着自行车继续走向商店.父亲贺明接到电话后（接电话时间忽略不计），立即骑车出发追赶小东，15分钟时追上小东，并修好了自行车，父亲贺明以原速返家，小东以原骑行速度骑车前往商店，10分钟时到达商店，此时两人相距5000米.

(1)、求父亲贺明和小东骑车的速度；

(2)、求小东家到商店的路程.

查看试题解析
23. 阅读下列材料解答问题：新定义：对非负数x“四舍五入”到个位的值记为＜x＞，即：当n为非负整数时，如果n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ ，则＜x＞＝n；反之，当n为非负整数时，如果＜x＞＝n，则n﹣ $\frac{1}{2}$ ≤x＜n+ $\frac{1}{2}$ .例如：＜0.1＞＝＜0.49＞＝0，＜1.51＞＝＜2.48＞＝2，＜3＞＝3，＜4.5＞＝＜5.25＞＝5，…试解决下列问题：

(1)、①＜π+2.4＞＝（π为圆周率）；②如果＜x﹣1＞＝2，则数x的取值范围为；

(2)、求出满足＜x＞＝ $\frac{5}{4}$ x﹣1的x的取值范围.

查看试题解析
24. 如图，四边形ABCD中，∠BAD＝106°，∠BCD＝64°，点M，N分别在AB，BC上，得 $△$ FMN，若MF∥AD，FN∥DC.

求：

(1)、∠F的度数；

(2)、∠D的度数.

查看试题解析
25. 某数码专营店销售A，B两种品牌智能手机，这两种手机的进价和售价如表所示：

A

B

进价（元/部）

3300

3700

售价（元/部）

3800

4300

(1)、该店销售记录显示，三月份销售A、B两种手机共34部，且销售A种手机的利润恰好是销售B种手机利润的2倍，求该店三月份售出A种手机和B种手机各多少部？

(2)、根据市场调研，该店四月份计划购进这两种手机共40部，要求购进B种手机数不低于A种手机数的 $\frac{3}{5}$ ，用于购买这两种手机的资金低于140000元，请通过计算设计所有可能的进货方案.

查看试题解析
26. 如图

(1)、如图1，△ABC中，∠ABC的平分线与外角∠ACD的平分线相交于P点，请探究∠P与∠A的关系，并说明理由.

(2)、如图2、3，四边形ABCD中，设∠A＝α，∠D＝β，∠P为四边形ABCD的内角∠ABC的平分线与外角∠DCE的平分线所在直线相交而形成的锐角.请利用（1）中的结论完成下列问题：
①如图2，若α+β＞180°，直接写出∠P的度数.（用α，β的代数式表示）

②如图3，若α+β＜180°，直接写出∠P的度数.（用α，β的代数式表示）

查看试题解析

	A	B
进价（元/部）	3300	3700
售价（元/部）	3800	4300