重庆市万盛经济技术开发区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-09-22 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,点(2,﹣4)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列调查中,适合采用全面调查(普查)方式的是( )A、对某班50名同学视力情况的调查 B、对元宵节期间市场上汤圆质量情况的调查 C、对某类烟花爆竹燃放质量情况的调查 D、对重庆嘉陵江水质情况的调查3. 下列图形都由若干个小图组成,其中可以由它的一个小图经过平移而得的图形是( )A、
 B、
B、 C、
C、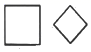 D、
D、 4. 如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )
4. 如图,点O为直线AB上一点,OC⊥OD.如果∠1=35°,那么∠2的度数是( )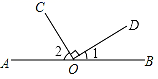 A、35° B、45° C、55° D、65°5. 在 , ,π, , ,0.1010010001…(相邻两个1之间0的个数逐次加1)这6个实数中,无理数的个数有( )A、2个 B、3个 C、4个 D、5个6. 已知二元一次方程组 如果用加减法消去n,那么下列方法可行的是( )A、4×①+5×② B、5×①+4×② C、5×①-4×② D、4×①-5×②7. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间8. 若方程ax﹣5y=3的一个解是 ,则a的值是( )A、13 B、﹣13 C、﹣7 D、79. 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )
A、35° B、45° C、55° D、65°5. 在 , ,π, , ,0.1010010001…(相邻两个1之间0的个数逐次加1)这6个实数中,无理数的个数有( )A、2个 B、3个 C、4个 D、5个6. 已知二元一次方程组 如果用加减法消去n,那么下列方法可行的是( )A、4×①+5×② B、5×①+4×② C、5×①-4×② D、4×①-5×②7. 黄金分割数 是一个很奇妙的数,大量应用于艺术、建筑和统计决策等方面,请你估算 ﹣1的值( )A、在1.1和1.2之间 B、在1.2和1.3之间 C、在1.3和1.4之间 D、在1.4和1.5之间8. 若方程ax﹣5y=3的一个解是 ,则a的值是( )A、13 B、﹣13 C、﹣7 D、79. 如图所示,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=20°,那么∠EFC′的度数为( )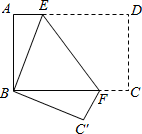 A、115° B、120° C、125° D、130°10. 我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )
A、115° B、120° C、125° D、130°10. 我国古代数学著作《九章算术》卷七有下列问题:“今有共买物,人出八,盈三:人出七,不足四,问人数、物价几何?”意思是:现在有几个人共同出钱去买件物品,如果每人出8钱,则剩余3钱:如果每人出7钱,则差4钱.问有多少人,物品的价格是多少?设有x人,物品的价格为y元,可列方程(组)为( )
A、 B、 C、 D、 =11. 如图,一个点在第一象限及x轴、y轴上移动,在第一秒钟,它从原点移动到点(1,0),然后按照图中箭头所示方向移动,即(0,0)→(1,0)→(1,1)→(0,1)→(0,2)→…,且每秒移动一个单位,那么第2020秒时,点所在位的坐标是( )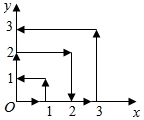 A、(64,44) B、(45,5) C、(44,5) D、(44,4)12. 如果关于x的不等式组 有且只有三个整数解,且关于x的方程2+a=3(4﹣x)有整数解,那么符合条件的所有整数a的和为( )A、﹣5 B、﹣6 C、﹣9 D、﹣13
A、(64,44) B、(45,5) C、(44,5) D、(44,4)12. 如果关于x的不等式组 有且只有三个整数解,且关于x的方程2+a=3(4﹣x)有整数解,那么符合条件的所有整数a的和为( )A、﹣5 B、﹣6 C、﹣9 D、﹣13二、填空题
-
13. 9的平方根是 ,使分式有意义的x的取值范围是 .14.
如图,若∠1=∠D=39°,∠C=51°,则∠B=°;
 15. 已知点A(m﹣1,m+4)在y轴上,则点A的坐标是.16. 某冷饮店一天售出各种口味冰淇淋份数的扇形统计图如图所示.则图中“芒果味”所在扇形的圆心角为.
15. 已知点A(m﹣1,m+4)在y轴上,则点A的坐标是.16. 某冷饮店一天售出各种口味冰淇淋份数的扇形统计图如图所示.则图中“芒果味”所在扇形的圆心角为.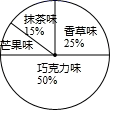 17. 有八个球编号是①至⑧,其中有六个球一样重,另外两个球都轻1克,为了找出这两个轻球,用天平称了三次,结果如下:第一次①+②比③+④重,第二次⑤+⑥比⑦+⑧轻,第三次①+③+⑤和②+④+⑧一样重.那么,两个轻球的编号是 .
17. 有八个球编号是①至⑧,其中有六个球一样重,另外两个球都轻1克,为了找出这两个轻球,用天平称了三次,结果如下:第一次①+②比③+④重,第二次⑤+⑥比⑦+⑧轻,第三次①+③+⑤和②+④+⑧一样重.那么,两个轻球的编号是 .
18. 自来水厂的供水池有7个进出水口,每天早晨6点开始进出水,且此时水池中有水15%,在每个进出水口是匀速进出的情况下,如果开放3个进口和4个出口,5小时将水池注满;如果开放4个进口和3个出口,2小时将水池注满.若某一天早晨6点时水池中有水24%,又因为水管改造,只能开放3个进口和2个出口,则从早晨6点开始经过小时水池的水刚好注满.三、解答题
-
19.(1)、计算:| | .(2)、解方程组: .20. 完成下面推理过程:
如图,已知DE∥BC,DF、BE分别平分∠ADE、∠ABC,可推得∠FDE=∠DEB的理由:
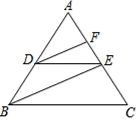
∵DE∥BC(已知)
∴∠ADE=▲ ( )
∵DF、BE分别平分∠ADE、∠ABC,
∴∠ADF= ▲ ( )
∠ABE= ▲ ( )
∴∠ADF=∠ABE
∴▲ ∥▲ ( )
∴∠FDE=∠DEB.( )
21. △ABC在平面直角坐标系中的位置如图所示.
( 1 )直接写出点A,B,C的坐标;
( 2 )将△ABC沿一定方向平移后,点A的对应点A'的坐标为(2,0),作出平移后的△A'B'C';
( 3 )求出△A'B'C'的面积.
22. 某校1200名学生参加了一场“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,整理并制作了如图所示的图表(部分未完成),请根据图表提供的信息,解答下列问题:分数段
频数
频率
30
0.1
90
0.4
60
0.2
(1)、本次调查的样本容量为;(2)、在表中, , ;(3)、补全频数分布直方图; (4)、如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?23. 小明解不等式 1的过程如图,
(4)、如果比赛成绩80分以上(含80分)为优秀,本次竞赛中笔试成绩为优秀的大约有多少名学生?23. 小明解不等式 1的过程如图,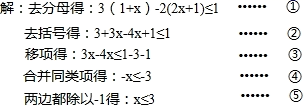
根据小明的解答过程,完成下列问题:
(1)、请指出他解答过程中有错误的步骤的序号;(2)、重新写出正确的解答过程;(3)、把不等式的解集在数轴上表示出来.24. 2020年1月底,武汉爆发“新冠”疫情,并开始向全国蔓延,出于防疫的需求,医用口罩迅速成为紧俏物资.某药店为解市民的燃眉之急,先后两次采购了A、B两种型号的医用口罩进行销售.已知这两种型号的医用口罩进货情况如表:第一次
第二次
A型口罩(箱)
20
30
B型口罩(箱)
30
40
累计采购款(元)
51000
72000
(1)、问A,B两种型号的口罩的进货单价各是多少元?(2)、销售中发现B型口罩的销量明显好于A型,药店在计划第三次采购时,决定购进B型口罩的箱数比A型口罩的箱数的2倍还多10箱,在采购总价不超过90000元的情况下,最多能购进多少箱B型口罩?25. 对非负实数x“四舍五入”到个位的值记为<x>.即:当n为非负整数时,如果n﹣0.5≤x<n+0.5,则<x>=n.
如:<0>=<0.48>=0,<0.64>=<1.493>=1,<2>=2.<3.5>=<4.12>=4,…
试解决下列问题:
(1)、填空:①<π>=(π为圆周率), ;②如果<2x﹣1>=3,则实数x的取值范围为;
(2)、求满足<x x的所有非负实数x的值.26. 如图,在长方形ABCD中,AB=8cm,BC=6cm,点E是CD边上的一点,且DE=2cm,动点P从A点出发,以2cm/s的速度沿A→B→C→E运动,最终到达点E.设点P运动的时间为t秒.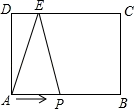 (1)、请以A点为原点,AB所在直线为x轴,1cm为单位长度,建立一个平面直角坐标系,并用t表示出点P在不同线段上的坐标.(2)、在(1)相同条件得到的结论下,是否存在P点使△APE的面积等于20cm2时,若存在,请求出P点坐标;若不存在,请说明理由.
(1)、请以A点为原点,AB所在直线为x轴,1cm为单位长度,建立一个平面直角坐标系,并用t表示出点P在不同线段上的坐标.(2)、在(1)相同条件得到的结论下,是否存在P点使△APE的面积等于20cm2时,若存在,请求出P点坐标;若不存在,请说明理由.