重庆市南岸区2019-2020学年七年级下学期数学期末考试试卷

试卷更新日期：2020-09-22 类型：期末考试

进入出卷网下载

一、选择题

1. 下列计算正确的是（）

A、 $a^{3} \cdot a^{3} = a^{6}$ B、 $a^{3} \cdot a^{3} = 2 a^{3}$ C、 $a^{3} \cdot a^{3} = a^{9}$ D、 $a^{3} + a^{3} = a^{6}$

查看试题解析
2. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 计算 ${(3 x)}^{2}$ 的结果是（）

A、 $3 x^{2}$ B、 $6 x^{2}$ C、 $9 x$ D、 $9 x^{2}$

查看试题解析
4. 任意掷一枚质地均匀的骰子，掷出的点数大于4的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
5. 如图，直线AB，CD相交于点O，EO⊥AB，若∠AOC=24°，则∠DOE的度数是（）

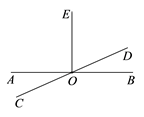A、24° B、54° C、66° D、76°

查看试题解析
6. 下列运用平方差公式计算，错误的是（）.

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 $(x + 1) (x - 1) = x^{2} - 1$ C、 $(2 x + 1) (2 x - 1) = 2 x^{2} - 1$ D、 $(- a + b) (- a - b) = a^{2} - b^{2}$

查看试题解析
7. 如图，在△ABC中，AD⊥BC，交BC的延长线于点D，BE⊥AC交AC的延长线于点E ，CF⊥BD交AB于点F.下列线段是△ABC的高的是（）

A、BD B、BE C、CE D、CF

查看试题解析
8. 为了测量池塘两侧A，B两点间的距离，在地面上找一点C，连接AC，BC，使∠ACB=90°，然后在BC的延长线上确定点D，使CD=BC，得到△ABC≌△ADC，通过测量AD的长，得AB的长.那么△ABC≌△ADC的理由是（）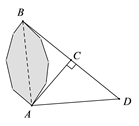

A、SAS B、AAS C、ASA D、SSS

查看试题解析
9. 在一段笔直的道路AB上，小李从A地出发，跑到B地，然后返回A地.小李距A地的距离 $y$ /m与其出发的时间 $x$ /分钟的关系，如图所示.下列说法错误的是（）

A、A，B两地的距离为1000m B、小李从A出发，4分钟跑到B地 C、小李从B返回A地时，每分钟跑 $\frac{500}{3}$ m D、小李到达B地后，休息了1分钟后返回A地

查看试题解析
10. 如图，AB $//$ EF，∠D=90°，则 $α$ ， $β$ ， $γ$ 的大小关系是（）

A、 $β = α + γ$ B、 $β = α + γ - 90 °$ C、 $β = γ + 90 ° - α$ D、 $β = α + 90 ° - γ$

查看试题解析
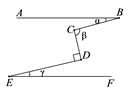11. 如图，在边长为a+b的正方形的四个角上，分别剪去直角边长分别为 $a$ ， $b$ 的四个直角三角形，则剩余部分面积，即图中的阴影部分的面积是（）

A、 $a^{2} - b^{2}$ B、 $2 a b$ C、 $a^{2} + b^{2}$ D、 $4 a b$

查看试题解析
12. 数学兴趣小组在一次数学活动课上，用一张面积为100cm²的正方形纸片制作了一副如图1所示的七巧板，并合作完成了如图2所示的作品.请计算图中①和②的面积之和是（）

A、12.5 cm² B、25 cm² C、37.5 cm² D、50 cm²

查看试题解析

二、填空题

13. 计算 $x^{6} \div x^{2} =$ .

查看试题解析
14. 新冠病毒是病毒的一种，病毒的体积微小，一般在电镜下才能见到.在病毒中，有一种病毒直径约0.000 000 021m，请用科学记数法把数0.000 000 021m表示出来.

查看试题解析
15. 小球在如图所示的地板上自由地滚动并随机地停留在某块方砖上，则它最终停留在黑砖上的概率是.

查看试题解析
16. 在△ABC中，用直尺和圆规在边BC上确定了一点D，并连接AD.若∠C=37°，根据作图痕迹，可求出∠ADB的度数是度.

查看试题解析
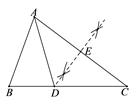17. 观察下列各式及其展开式：
${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ ，

${(a + b)}^{3} = a^{3} + 3 a^{2} b + 3 a b^{2} + b^{3}$ ，

${(a + b)}^{4} = a^{4} + 4 a^{3} b + 6 a^{2} b^{2} + 4 a b^{3} + b^{4}$ ，

${(a + b)}^{5} = a^{5} + 5 a^{4} b + 10 a^{3} b^{2} + 10 a^{2} b^{3} + 5 a b^{4} + b^{5}$ ，……

根据其中的规律，请你猜想 ${(a + b)}^{7}$ 的展开式中第四项的系数是.

查看试题解析
18. 我们知道，一个两位数的十位数字为 $a$ ，个位数字为 $b$ ，其中 $0 < a \leq 9$ ， $0 \leq b \leq 9$ ，且 $a$ ， $b$ 都为整数，这个两位数可以表示为 $10 a + b$ .观察下列各式：2323÷101=23，4545÷101=45，5151÷101=51，7979÷101=79，……，根据以上等式，猜想： $(1010 a + 101 b) \div (10 a + b) =$ .

查看试题解析

三、解答题

19. 计算：

(1)、 $x (x - 2 y) + {(x + y)}^{2}$ ；

(2)、 $(a + b) (a - b) + (2 a b^{3} - 4 a^{2} b^{2}) \div 2 a b$ .

查看试题解析
20. 已知三角形的两边及其夹角，求作这个三角形.
已知：线段 $m$ ， $n$ ，∠ $β$ .

求作：△ABC，使AB= $m$ ，BC= $n$ ，∠ABC=∠ $β$ （保留作图痕迹，不写作法）.

查看试题解析

21. 疫情之后，各大商家为吸引顾客，纷纷采用多种促销手段.其中一个商场设立了一个购物满50元，可以获得一次转动转盘的机会，当转盘停止时，指针落在那个区域就可以得到相应的奖品.下表是活动进行中的一组统计数据：

转动转盘的次数	100	200	500	1000	1500	2000
落在“抽纸”的次数 $n$	51	99	251	502	750	1002
落在“抽纸”的频率 $\frac{n}{m}$

(1)、完成上表；

(2)、请估计，当

m

很大时，频率是多少？

(3)、假如你去转动转盘一次，你获得“抽纸”的概率是多少？

查看试题解析

22. 如图， AC平分∠MAE，交DB于点F.

(1)、若AB∥CE，∠BAE=50°，求∠ACE的度数；

(2)、若∠AFB=∠CAM，说明∠ACE=∠BDE的理由.

查看试题解析
23. 如图，在△ABC中，点D是BC上一点，且AD=AB，AE∥BC，∠BAD=∠CAE，连接DE交AC于点F.

(1)、若∠B=70°，求∠C的度数；

(2)、若AE=AC，AD平分∠BDE是否成立？请说明理由.

查看试题解析

24. 为了鼓励居民节约用水，某市采用“阶梯水价”的方法按月计算每户家庭的水费，设每户家庭用水量为

x

吨时，应交水费

y

元.如图，是用水量不大于

a

吨时，所交的水费

y

/元与用水量

x

/吨之间的关系.当用水量

x > a

时，所交的水费

y

/元与用水量

x

/吨之间的关系如下表所示.

用水量 $x$ /吨	21	22	23	24	25	26	27	…
水费 $y$ /元	42.8	45.6	48.4	51.2	54	56.8	59.6	…

(1)、直接写出

a

的值，并分别求出

0 \leq x \leq a

和

x > a

时，

y

与

x

之间的关系式；

(2)、小颖家4月、5月分别交水费38元，68元，问小颖家5月份比4月份多用多少吨水？

查看试题解析

25. 在∠MAN内有一点D，过点D分别作DB⊥AM，DC⊥AN，垂足分别为B，C.且BD=CD，点E，F分别在边AM和AN上.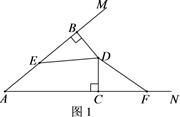

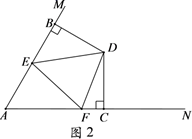(1)、如图1，若∠BED=∠CFD，请说明DE=DF；

(2)、如图2，若∠BDC=120°，∠EDF=60°，猜想EF，BE，CF具有的数量关系，并说明你的结论成立的理由.

查看试题解析
26. 如图所示，在街道 $l$ 的同一侧，有两个居民区A，B，两个居民区门口到街道的距离分别为AC，BD.现准备在街道 $l$ 旁设置一个快递中转站.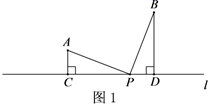

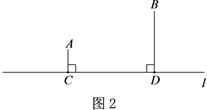
(1)、如果设置的快递中转站到A，B两个小区的距离相等，如图1，当∠A=∠BPD时，请说明AC+BD=CD的理由；

(2)、如果设置的快递中转站到A，B两个小区的距离之和最短，请在图2中作出点P的位置，连接AP，BP，直接写出此时∠PAC与∠PBD的数量关系；

(3)、为了能错峰进行取送快递，决定设置的快递中转站到A，B两个小区的距离之差最大，请在图3中作出点P的位置，连接AP，BP，直接写出此时∠PAC与∠PBD的数量关系.

查看试题解析