江苏省无锡市锡山区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-09-22 类型:期末考试
一、选择题
-
1. 下列运算中,正确的是( )A、(ab2)2=a2b4 B、a2+a2=2a4 C、a2•a3=a6 D、a6÷a3=a22. 若a b,则下列式子错误的是( )A、 B、 C、 D、3. 下列等式从左到右的变形,属于因式分解的是( )A、a(x-y)=ax-ay B、x2-1=(x+1)(x-1) C、(x+1)(x+3)=x2+4x+3 D、x2+2x+1=x(x+2)+14. 的计算结果是( )A、 B、 C、 D、5. 若三角形的三边长分别为4、x、7,则x的值可以是( )A、2 B、3 C、8 D、116. 已知 是关于x、y的方程2x y+3k=0的解,则k的值为( )A、 1 B、2 C、0 D、17. 不等式组 的解集在数轴上表示为A、
 B、
B、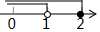 C、
C、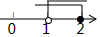 D、
D、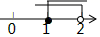 8. 用一根长80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm.设这个长方形的长为xcm、宽为ycm,列出关于x、y的二元一次方程组,下列正确的是( )A、 B、 C、 D、9. 如图,矩形纸片ABCD沿着BE折叠,使C、D两点分别落在C1、D1处,若∠ABC1=45°,则∠ABE的度数为( )
8. 用一根长80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm.设这个长方形的长为xcm、宽为ycm,列出关于x、y的二元一次方程组,下列正确的是( )A、 B、 C、 D、9. 如图,矩形纸片ABCD沿着BE折叠,使C、D两点分别落在C1、D1处,若∠ABC1=45°,则∠ABE的度数为( )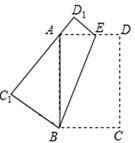 A、22.5° B、21.5° C、22° D、21°10. 如图,在△ABC中,AG=BG,BD=DE=EC,CF=4AF,若四边形DEFG的面积为14,则△ABC的面积为( )
A、22.5° B、21.5° C、22° D、21°10. 如图,在△ABC中,AG=BG,BD=DE=EC,CF=4AF,若四边形DEFG的面积为14,则△ABC的面积为( )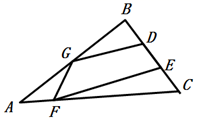 A、24 B、28 C、35 D、30
A、24 B、28 C、35 D、30二、填空题
-
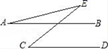
11. 新型冠状肺炎病毒(COVID﹣19)的粒子,其直径在120~140纳米即0.00000012米~0.00000014米之间,数据0.00000012用科学记数法可以表示为.12. 若am=9,an=3,则am-n=.13. 如果一个n边形的内角和是1440°,那么n= .14. 不等式 的正整数解为.15. 如图,若AB∥CD,∠C=60°,则∠A+∠E=度.
 16. 如果 ,那么 的逆命题是.17. 计算: .18. 如果三角形的两个内角α与β满足3α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,B、C为直线l上两点,点A在直线l外,且∠ABC=45°.若P是l上一点,且△ABP是“准直角三角形”,则∠APB的所有可能的度数为.
16. 如果 ,那么 的逆命题是.17. 计算: .18. 如果三角形的两个内角α与β满足3α+β=90°,那么我们称这样的三角形为“准直角三角形”.如图,B、C为直线l上两点,点A在直线l外,且∠ABC=45°.若P是l上一点,且△ABP是“准直角三角形”,则∠APB的所有可能的度数为.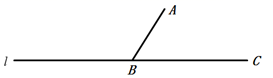
三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 把下列各式因式分解:(1)、mx2﹣my2;(2)、 .21.(1)、解方程组:(2)、解不等式组:22. 先化简,再求值:
,其中 .
23. 如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.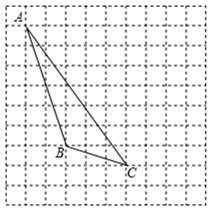 (1)、①画出△ABC向下平移1个单位,再向右平移4个单位后的图形△ ;
(1)、①画出△ABC向下平移1个单位,再向右平移4个单位后的图形△ ;②画出△ABC的AB边上的高CD,垂足为D;
(2)、求出△ABC的面积为;(3)、图中,能使S△QBC=3的格点Q,共有个.24. 新冠肺炎疫情期间,某口罩厂为生产更多的口罩满足疫情防控需求,决定拨款560万元购进A,B两种型号的口罩机共30台.两种型号口罩机的单价和工作效率分别如表: (1)、求购进A,B两种型号的口罩机各多少台;(2)、现有200万只口罩的生产任务,计划安排新购进的口罩机共15台进行生产.若工厂的工人每天工作10h,则至少购进B种型号的口罩机多少台才能在5天内完成任务?25. 定义一种新运算“a b”:当a≥b时,a b=a+2b;当a<b时,a b=a-2b.例如:3 (-4)=3 , .(1)、填空:(-3) (-2)=;(2)、若 则x的取值范围为;(3)、已知 ,求x的取值范围;(4)、利用以上新运算化简: .26. 如图1,已知直线MN GH,且MN和GH之间的距离为1,小明同学制作了两个直角三角形硬纸板ACB和DEF,其中∠ACB=90°,∠DFE=90°,∠BAC=45°,∠EDF=30°,AC=1.小明利用这两块三角板进行了如下的操作探究:
(1)、求购进A,B两种型号的口罩机各多少台;(2)、现有200万只口罩的生产任务,计划安排新购进的口罩机共15台进行生产.若工厂的工人每天工作10h,则至少购进B种型号的口罩机多少台才能在5天内完成任务?25. 定义一种新运算“a b”:当a≥b时,a b=a+2b;当a<b时,a b=a-2b.例如:3 (-4)=3 , .(1)、填空:(-3) (-2)=;(2)、若 则x的取值范围为;(3)、已知 ,求x的取值范围;(4)、利用以上新运算化简: .26. 如图1,已知直线MN GH,且MN和GH之间的距离为1,小明同学制作了两个直角三角形硬纸板ACB和DEF,其中∠ACB=90°,∠DFE=90°,∠BAC=45°,∠EDF=30°,AC=1.小明利用这两块三角板进行了如下的操作探究: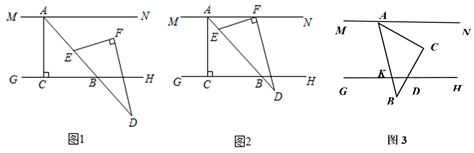 (1)、如图1,点A在MN上,边BC在GH上,边DE在直线AB上.
(1)、如图1,点A在MN上,边BC在GH上,边DE在直线AB上.①将直角三角形DEF沿射线BA的方向平移,当点F在MN上时,如图2,求∠AFE的度数;
②将直角三角形DEF从图2的位置继续沿射线BA的方向平移,当以A、D、F为顶点的三角形是直角三角形时,求∠FAN度数;
(2)、将直角三角形ABC如图3放置,若点A在直线MN上,点C在MN和GH之间(不含MN,GH上),边BC和AB与直线GH分别交于D,K.在△ABC绕着点A旋转的过程中,设∠MAK=n°,∠CDK=(4m﹣2n﹣10)°,则m的取值范围为.