江苏省南通市崇川区港闸区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-09-22 类型:期末考试
一、选择题
-
1. 9的平方根是( )A、3 B、 C、±3 D、2. 将点A(2,1)向左平移2个单位长度得到点A′,则点A′的坐标是( )
A、(2,3) B、(2,-1) C、(4,1) D、(0,1)3. 下列调查方式,你认为最合适的是( )A、日光灯管厂要检测一批灯管的使用寿命,采用普查方式 B、了解衢州市每天的流动人口数,采用抽查方式 C、了解衢州市居民日平均用水量,采用普查方式 D、旅客上飞机前的安检,采用抽样调查方式4. 下列x,y的各对数值中,是方程组 的解的是( )A、 B、 C、 D、5. 若x>y,则下列式子中正确的是( )A、x﹣2>y﹣2 B、x+2<y+2 C、﹣2x>﹣2y D、6. △ABC中,AB=3,AC=2,BC=a,下列数轴中表示的a的取值范围,正确的是( )A、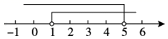 B、
B、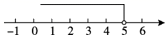 C、
C、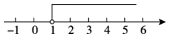 D、
D、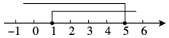 7. 有一个数值转换器,流程如下:
7. 有一个数值转换器,流程如下: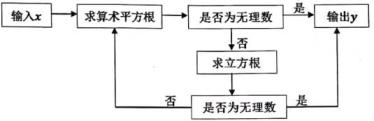
当输入x的值为64时,输出y的值是( )
A、2 B、2 C、 D、8.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是( )
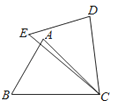 A、BC=EC,∠B=∠E B、BC=EC,AC=DC C、BC=DC,∠A=∠D D、∠B=∠E,∠A=∠D9. 如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是( )
A、BC=EC,∠B=∠E B、BC=EC,AC=DC C、BC=DC,∠A=∠D D、∠B=∠E,∠A=∠D9. 如图,在四边形ABCD中,对角线AC平分∠BAD,AB>AD,下列结论中正确的是( )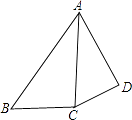 A、AB﹣AD>CB﹣CD B、AB﹣AD=CB﹣CD C、AB﹣AD<CB﹣CD D、AB﹣AD与CB﹣CD的大小关系不确定10. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )
A、AB﹣AD>CB﹣CD B、AB﹣AD=CB﹣CD C、AB﹣AD<CB﹣CD D、AB﹣AD与CB﹣CD的大小关系不确定10. 如图,在平面直角坐标系xOy中,点P(1,0).点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(﹣1,1),第3次向上跳动1个单位至点P3 , 第4次向右跳动3个单位至点P4 , 第5次又向上跳动1个单位至点P5 , 第6次向左跳动4个单位至点P6 , ….照此规律,点P第100次跳动至点P100的坐标是( )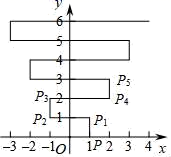 A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)
A、(﹣26,50) B、(﹣25,50) C、(26,50) D、(25,50)二、填空题
-
11. 若 在实数范围内有意义,则x的取值范围是 .12. 一个多边形的内角和是外角和的2倍,则这个多边形的边数为 .13. 如图,∠C=90°,AD平分∠BAC交BC于点D,若BC=5cm,BD=3cm,则D到AB的距离为.
 14. 在平面直角坐标系中,若点M(﹣2,3)与点N(x,3)之间的距离是5,则x的值是.15. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为 .16. 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为.
14. 在平面直角坐标系中,若点M(﹣2,3)与点N(x,3)之间的距离是5,则x的值是.15. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?”其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱.现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为 .16. 如图,AD是△ABC的角分平线,CE是△ABC的高,∠BAC=60°,∠BCE=50°,点F为边AB上一点,当△BDF为直角三角形时,则∠ADF的度数为. 17. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是.
17. 如图,在△ABC中,∠BAC=90°,AD是高,BE是中线,CF是角平分线,CF交AD于点G,交BE于点H,下面说法中正确的序号是.①△ABE的面积等于△BCE的面积;②∠AFG=∠AGF;③∠FAG=2∠ACF;④BH=CH.
 18. 已知关于 的不等式组 的整数解恰有 个,则 的取值范围是.
18. 已知关于 的不等式组 的整数解恰有 个,则 的取值范围是.三、解答题
-
19.(1)、解方程组 ;(2)、解不等式组
把其解集在数轴上表示出来,并写出它的所有负整数解.
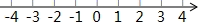 20. 已知:x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根.21. 已知:如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=28°,求∠DAE的度数.
20. 已知:x﹣2的平方根是±2,2x+y+7的立方根是3,求x2+y2的算术平方根.21. 已知:如图,在△ABC中,∠BAC=100°,AD⊥BC于D点,AE平分∠BAC交BC于点E.若∠C=28°,求∠DAE的度数.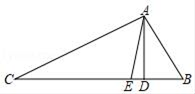 22. 2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战,其中,A社区有500名在职党员,为了解本社区2月﹣3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
22. 2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战,其中,A社区有500名在职党员,为了解本社区2月﹣3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.应急执勤次数的频数分布表
次数x/次
频数
0≤x<10
8
10≤x<20
10
20≤x<30
16
30≤x<40
a
x≥40
4
其中,应急执勤次数在20≤x<30这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
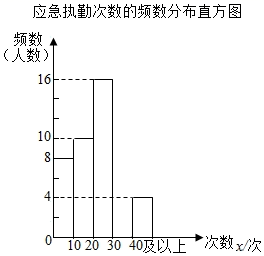
请根据所给信息,解答下列问题:
(1)、a=;(2)、请补全频数分布直方图;(3)、将随机抽取的50名在职党员参加应急执勤次数按由小到大顺序排列,处于最中间位置的次数(或最中间位置的次数的平均数)等于;(4)、请估计2月﹣3月期间A社区在职党员参加应急执勤的次数不低于30次的约有人.23. 证明:如果两个三角形有两个角及它们的夹边的高分别相等,那么这两个三角形全等.24. 先阅读下列一段文字,再回答问题.已知平面内两点P1(x1 , y1),P2(x2 , y2),这两点的距离P1P2 .同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)、已知点A(2,4),B(﹣3,﹣8),试求A,B两点间的距离;(2)、已知点A,B所在的直线平行于y轴,点B的纵坐标为﹣1,A,B两点间的距离等于6.试求点A的纵坐标;(3)、已知一个三角形各顶点的坐标分别为A(﹣3,﹣2),B(3,6),C(7,﹣2),你能判断三角形ABC的形状吗?说明理由.25. 某治污公司决定购买10台污水处理设备.现有甲、乙两种型号的设备可供选择,其中每台的价格与月处理污水量如下表:甲型
乙型
价格(万元/台)
x
y
处理污水量(吨/月)
300
260
经调查:购买一台甲型设备比购买一台乙型设备多2万元,购买3台甲型设备比购买4台乙型设备少2万元.
(1)、求x,y的值;(2)、如果治污公司购买污水处理设备的资金不超过91万元,求该治污公司有哪几种购买方案;(3)、在(2)的条件下,如果月处理污水量不低于2750吨,为了节约资金,请为该公司设计一种最省钱的购买方案.26. 如果一元一次方程的解也是一元一次不等式组的解,则称该一元一次方程为该不等式组的相关方程.例如:方程2x﹣6=0的解为x=3,不等式组 的解集为2<x<5,因为2<3<5,所以称方程2x﹣6=0为不等式组 的相关方程.
(1)、在方程①5x﹣2=0,② x+3=0,③x﹣(3x+1)=﹣5中,不等式组 的相关方程是;(填序号)(2)、若不等式组 的一个相关方程的解是整数,则这个相关方程可以是;(写出一个即可)(3)、若方程2x﹣1.5=x+2,6+x=2(x )都是关于x的不等式组 的相关方程,求m的取值范围.