江苏省南京市鼓楼区2019-2020学年七年级下学期数学期末考试试卷
试卷更新日期:2020-09-22 类型:期末考试
一、选择题
-
1. 下列各式,计算结果为a6的是( )A、a2+a4 B、a7¸a C、a2×a3 D、(a2)42. 氢原子的半径约为0.00000000005m,该数用科学记数法可以表示为( )A、5´10-9 B、0.5´10-10 C、5´10-11 D、5´10-123. 若a>b,则下列不等式中,一定正确的是( )A、 B、-2a>-2b C、a2>b2 D、4. 下列命题与它的逆命题均为真命题的是( )A、内错角相等 B、对顶角相等 C、如果ab=0,那么a=0 D、互为相反数的两个数和为05. 一辆汽车从 地驶往 地,前 路段为普通公路,其余路段为高速公路,已知汽车在普通公路上行驶的速度为 ,在高速公路上行驶的速度为 ,汽车从 地到 地一共行驶了 .设普通公路长、高速公路长分别为 ,则可列方程组为( )A、 B、 C、 D、6. 如图,在四边形ABCD中,连接BD,下列判断正确的是( )
 A、若∠1=∠2,则AB//CD B、若∠3=∠4,则AD//BC C、若∠A+∠ABC=180°,则AB//CD D、若∠A=∠C,∠ABC=∠ADC,则AB//CD
A、若∠1=∠2,则AB//CD B、若∠3=∠4,则AD//BC C、若∠A+∠ABC=180°,则AB//CD D、若∠A=∠C,∠ABC=∠ADC,则AB//CD二、填空题
-
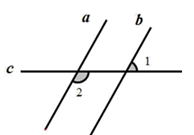
7. 计算:5-1= , 50=.8. 如图,直线a,b被直线c所截,∠1=40°.要使a∥b,则∠2的度数应为.
 9. 计算: .10. 若(x+y)2=5,xy=2,则x2+y211. 如果有理数x,y满足方程组 那么x2-y2=.12. 如图,CD//AB,若∠ECB=92°,∠B=57°,则∠1=°
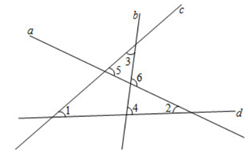
9. 计算: .10. 若(x+y)2=5,xy=2,则x2+y211. 如果有理数x,y满足方程组 那么x2-y2=.12. 如图,CD//AB,若∠ECB=92°,∠B=57°,则∠1=°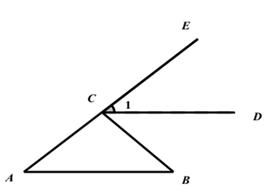 13. 若关于x的不等式组 ,有3个整数解,则a的取值范围是.14. 如图,直线a、b、c、d互不平行,以下结论正确的是.(只填序号)
13. 若关于x的不等式组 ,有3个整数解,则a的取值范围是.14. 如图,直线a、b、c、d互不平行,以下结论正确的是.(只填序号)① ∠ 1+ ∠ 2= ∠ 5;② ∠ 1+ ∠ 3= ∠ 4;
③ ∠ 1+ ∠ 2+ ∠ 3= ∠ 6;④ ∠ 3+ ∠ 4= ∠ 2+ ∠ 5.
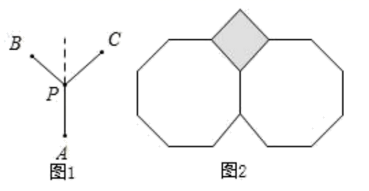
 15. 如图1,作 ∠ BPC平分线的反向延长线PA,以 ∠ APB,∠APC,∠BPC为内角可以分别作三个边长相等的正多边形.
15. 如图1,作 ∠ BPC平分线的反向延长线PA,以 ∠ APB,∠APC,∠BPC为内角可以分别作三个边长相等的正多边形.例如:若∠BPC=90°,则∠APB=∠APC=135°,图2就是一个符合要求的图形.
在所有符合要求的图形中,∠BPC的度数是.(∠BPC=90°除外)
三、解答题
-
16. 计算:(1)、(-a)5×a2+a×(-a6)(2)、(y-2x)(x+2y)17. 先化简,再求值:(x-1)2-2(x+3)(x-3)+x(x-4),其中x=3.18. 分解因式:(1)、4x2-12x+9(2)、x2(3y-6)+x(6-3y)19. 已知4x+y=1(1)、y=.(用含x的代数式表示)(2)、当y为非负数时,x的取值范围是.(3)、当-1<y≤2时,求x的取值范围.20. 解方程组 .21.(1)、分别画出图中△ABC的角平分线AF(点F在BC上)、中线BD(点D在AC上)和高CE(E为垂足).
 (2)、根据(1)中的要求,回答下列问题:
(2)、根据(1)中的要求,回答下列问题:①面积一定相等的三角形是(不添加字母和辅助线);
②若∠BAC=120°,则∠AFC+∠FCE=°
22. 如图,点D、E分别在AB、BC上,AF//BC,∠1=∠2.试证明:DE//AC(请写出每一步的证明依据)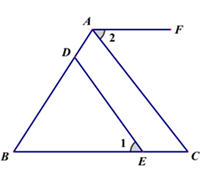 23. 甲、乙两人各有图书若干,如果甲从乙那里拿来10本,那么甲拥有图书的本数是乙所剩本数的5倍;如果乙从甲那里拿来10本,那么乙拥有的图书的本数与甲所剩的本数相等.甲乙两人原来分别有多少本图书?(1)、设甲原来有x本图书,乙原来有y本图书,完成下表:
23. 甲、乙两人各有图书若干,如果甲从乙那里拿来10本,那么甲拥有图书的本数是乙所剩本数的5倍;如果乙从甲那里拿来10本,那么乙拥有的图书的本数与甲所剩的本数相等.甲乙两人原来分别有多少本图书?(1)、设甲原来有x本图书,乙原来有y本图书,完成下表:甲从乙那里拿来10本
乙从甲那里拿来10本
甲拥有的图书
x+10
乙拥有的图书
y+10
(2)、根据以上信息列方程组解决上述问题.24. 用两种方法证明“三角形的外角和等于360°”;如图,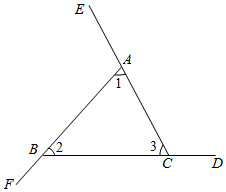
∠BAE、∠CBF、∠ACD是△ABC的三个外角.求证:∠BAE+∠CBF+∠ACD=360°
证法1:∵∠BAE、∠CBF、∠ACD是△ABC的三个外角
∴__▲_.
∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3)
∵_▲_.
∴∠BAE+∠CBF+∠ACD=360°
请把证法1补充完整,并用不同的方法完成证法2
25. 2020年2月,为了应对武汉发生的新型冠状病毒疫情,国家卫健委及相关单位在武汉建立了方舱医院,某方舱医院的具体信息如下:( 1 )方舱医院由四部分组成,分别是废弃物处理单元、病房单元、技术保障单元、医疗功能单元;
( 2 )整个方舱医院占地面积为80000平方米;
( 3 )废弃物处理单元面积为总占地面积的5%;
( 4 )病房单元占地面积是技术保障单元占地面积的4倍;
( 5 )病房单元与医疗功能单元面积的和不高于总占地面积的85%,求医疗功能单元的最大面积.
26. 在∠MAN的两边上各取点B、C,在平面上任取点P(不与点A、B、C重合),连接PB、PC,设∠BPC为∠1,∠ABP为∠2,∠ACP为∠3.请探索∠1、∠2、∠3和∠BAC这4个角之间的数量关系.分析问题:由于点P是平面上的任意点,要考虑全面,需对点P的位置进行如下分类.
(1)、若点P在∠MAN的两边上,易知点B、C将两边分成线段AB、AC,射线BM、CN四个部分,根据提示,完成表格;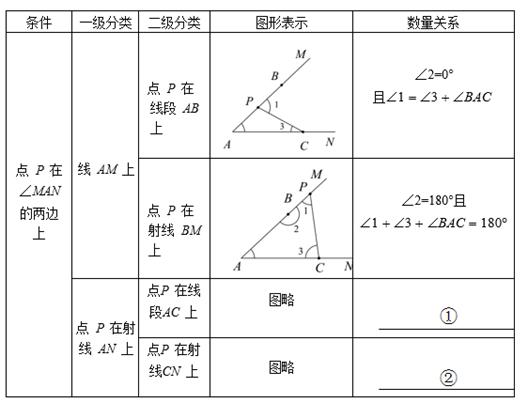
①;②。
(2)、点P在∠MAN的内部,如图1,线段BC将内部分成线段BC,区域①,区域②三个部分.若点P在线段BC上,则所求数量关系:∠1=180°且∠2+∠3+∠BAC=180°;若点P在区域①中,则所求数量关系为:▲ ;
若点P在区域②中,写出这4个角之间的数量关系,并利用图2加以证明.
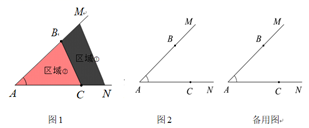 (3)、类比解决:
(3)、类比解决:点P在∠MAN的外部时,直接写出当点P在该部分时这4个角之间的数量关系.