天津市武清区2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-09-21 类型：期中考试
一、单选题
-
1. 下列四个图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列线段能组成三角形的是（ ）A、3、4、8 B、5、6、11 C、5、6、10 D、2、2、43. 如果n边形的内角和是它外角和的4倍，则n等于（ ）A、7 B、8 C、10 D、94. 若等腰三角形的一边长等于6，另一边长等于4，则它的周长等于（ ）A、15或17 B、16 C、14 D、14或165. 下列说法正确的是（ ）A、能够完全重合的三角形是全等三角形 B、面积相等的三角形是全等三角形 C、周长相等的三角形是全等三角形 D、所有的等边三角形都是全等三角形6. 已知：点P、Q是△ABC的边BC上的两个点，且BP=PQ=QC=AP=AQ，∠BAC的度数是（ ）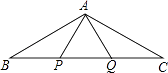
A、100° B、120° C、130° D、150°7.如图，在△ABC和△DEC中，已知AB=DE，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是（ ）
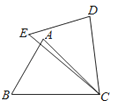A、BC=EC，∠B=∠E B、BC=EC，AC=DC C、BC=DC，∠A=∠D D、∠B=∠E，∠A=∠D8. 如图，在Rt△ABC中，∠ACB=90°，BD平分∠ABC．若CD=3，BC+AB=16，则△ABC的面积为（ ）
A、16 B、18 C、24 D、329. 如图，在△ABC 中，AB = AC ， E 、D 分别为 AB 、AC 边上的中点，连接 BD 、CE 交于O ， 此图中全等三角形的对数为（ ） 对．
A、4 B、3 C、2 D、110. 下列说法正确的是（ ）A、任何一个图形都有对称轴 B、两个全等三角形一定关于某直线对称 C、若△ABC与△A′B′C′成轴对称，则△ABC≌△A′B′C′ D、点A，点B在直线1两旁，且AB与直线1交于点O，若AO=BO，则点A与点B关于直线l对称11. 如图，在锐角三角形ABC中，直线l为BC的中垂线，射线m为∠ABC的角平分线，直线l与m相交于点P.若∠BAC＝60°，∠ACP＝24°，则∠ABP的度数是（ ）
A、24° B、30° C、32° D、36°12. 如图，等边△ABC的边长为4，AD是边BC上的中线，F是边AD上的动点，E是边AC上一点，若AE=2，则EF+CF取得最小值时，∠ECF的度数为（ ）
A、15° B、22.5° C、30° D、45°二、填空题
-
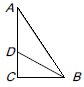
13. 等腰三角形的一个角100°，它的另外两个角的度数分别为14. 若A（x，3）关于y轴的对称点是B（－2，y），则x= ,y= ,点A关于x轴的对称点的坐标是 。15. 从八边形的一个顶点出发可以画出条对角线，内角和为 ．16. 如图 ，在△ ABC 中，∠C＝90°，∠ABC 的平分线 BD 交 AC 于点 D．若 BD＝10cm，BC＝8cm，则点 D 到直线 AB 的距离= ．
17. 如图，在△ABC中，AC＝8，BC＝5，AB的垂直平分线DE交AB于点D，交边AC于点E，则△BCE的周长为 ．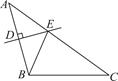
18. 如图所示，△ABC为等边三角形，AQ＝PQ，PR＝PS，PR⊥AB于R，PS⊥AC于S，则四个结论正确的是 ．①P在∠A的平分线上； ②AS＝AR； ③QP∥AR； ④△BRP≌△QSP．
三、解答题
-
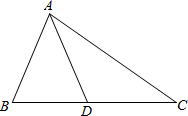
19. 如图，△ABC中，AB＝AD＝DC，∠BAD＝40°，求∠B、∠C的度数.
20. △ABC在平面直角坐标系中的位置如图所示，点A(−2，2)，点B(−3，−1)，点C(−1，1).
(1)、画出△ABC关于y轴对称的△A1B1C1 ， 并写出点A1的坐标.(2)、求出△A1B1C1的面积.21. 已知AB＝AC，BD＝CE，求证：∠B＝∠C．
22. 已知：AB＝CD，AE⊥BC于E，DF⊥BC于F，且CE＝BF ．求证：AB∥CD．
