重庆市万州区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-21 类型:期末考试
一、选择题
-
1. 下列各式中,属于分式的是( )A、 B、 C、 D、2. 下列四边形中,不属于轴对称图形的是( )A、平行四边形 B、矩形 C、菱形 D、正方形3. 把分式 中 的值都同时扩大到原来的5倍,则分式的值( )A、缩小到原来的5倍 B、扩大到原来5倍 C、不变 D、扩大到原来25倍4. 在平面直角坐标系中,点 关于 轴对称的点的坐标为( )A、 B、 C、 D、5. 下列命题为真命题的是( )A、对角线互相垂直的四边形是矩形 B、对角线相等的四边形是矩形 C、四条边都相等的四边形是矩形 D、四个角都相等的四边形是矩形6. 如图是用程序计算函数值,若输入 , 则输出的 的值为( )
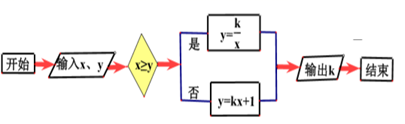 A、 B、6 C、 D、7. 如图,在 中, 分别为 上一点,延长 至 ,使得 ,若 则 的长为( )
A、 B、6 C、 D、7. 如图,在 中, 分别为 上一点,延长 至 ,使得 ,若 则 的长为( )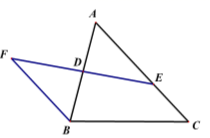 A、0.5 B、1 C、1.5 D、28. 若 ,则 的值是( )A、 B、 C、-16 D、9. 如图,菱形 中,在边 上分别截取 ,连接 交 于点 ,连接 ,若 ,则 的度数为( )
A、0.5 B、1 C、1.5 D、28. 若 ,则 的值是( )A、 B、 C、-16 D、9. 如图,菱形 中,在边 上分别截取 ,连接 交 于点 ,连接 ,若 ,则 的度数为( )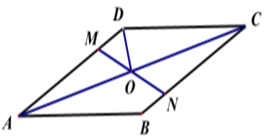 A、 B、 C、 D、10. 已知四边形 是矩形,边 在 轴上,边 在 轴上,反比例函数 经过矩形 对角线的交点 .若 的面积为 ,则 的值是( )
A、 B、 C、 D、10. 已知四边形 是矩形,边 在 轴上,边 在 轴上,反比例函数 经过矩形 对角线的交点 .若 的面积为 ,则 的值是( )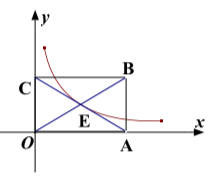 A、10 B、5 C、 D、11. 若实数 使得关于 的分式方程 的解为负数,且使得关于 的一次函数 过第一、二、三象限.则符合条件的所有整数 的和为( )A、6 B、5 C、3 D、212. 如图,在边长为 的正方形纸片 中, 是边 上的一点, 连结 ,将正方形纸片折叠,使点 落在线段 上的点 处,折痕为 .则 的长为( )
A、10 B、5 C、 D、11. 若实数 使得关于 的分式方程 的解为负数,且使得关于 的一次函数 过第一、二、三象限.则符合条件的所有整数 的和为( )A、6 B、5 C、3 D、212. 如图,在边长为 的正方形纸片 中, 是边 上的一点, 连结 ,将正方形纸片折叠,使点 落在线段 上的点 处,折痕为 .则 的长为( )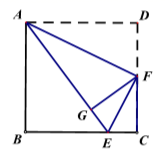 A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
13. 计算: .14. 万州区九池乡盛产草莓,每年三四月正是草莓成熟的季节.某水果经销商为了更好地了解市场,分别对甲、乙、丙、丁四个市场四月份每天出售的草莓价格进行调查,通过计算发现这个月四个市场草莓的平均售价相同,方差分别为 ,则该经销商四月份草莓价格最稳定的市场是.15. 如图所示,一次函数y=kx+3的图象经过点(2,0),则关于x的不等式kx+3>0的解集是 .
 16. 如图,在菱形 中, ,以 边作正方形 交于点 ,则图中阴影部分的面积为.
16. 如图,在菱形 中, ,以 边作正方形 交于点 ,则图中阴影部分的面积为. 17. 高峡平湖,平湖万州.万州变得越来越漂亮,一天晚饭后,小浩和他爸爸同时从家出发沿相同路线不同的速度到离家2400米的滨江公园散步,当小浩途中经过音乐喷泉广场时,音乐喷泉恰好开放,于是小浩停下脚步观看了一会儿音乐喷泉后,继续以先前的速度前往公园,爸爸途径音乐喷泉广场时看见小浩,挥手示意后继续向公园方向前行,最终小浩比爸爸晚到 分钟,如图是两人之间的距离 (米)与爸爸行走的时间 (分钟)之间的函数关系,则小浩在音乐喷泉广场观看音乐喷泉分钟.
17. 高峡平湖,平湖万州.万州变得越来越漂亮,一天晚饭后,小浩和他爸爸同时从家出发沿相同路线不同的速度到离家2400米的滨江公园散步,当小浩途中经过音乐喷泉广场时,音乐喷泉恰好开放,于是小浩停下脚步观看了一会儿音乐喷泉后,继续以先前的速度前往公园,爸爸途径音乐喷泉广场时看见小浩,挥手示意后继续向公园方向前行,最终小浩比爸爸晚到 分钟,如图是两人之间的距离 (米)与爸爸行走的时间 (分钟)之间的函数关系,则小浩在音乐喷泉广场观看音乐喷泉分钟.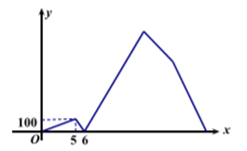 18. 如图,已知AB=12米,MA⊥AB于点A,MA=6米,射线BD⊥AB于点B,点P从点B出发沿BA方向往点A运动,每秒走1米,点Q从点B出发沿BD方向运动,每秒走2米,若点P、Q同时从点B出发,出发t秒后,在线段MA上有一点C,使由点C、A、P组成的三角形与△PBQ全等,则t的值是.
18. 如图,已知AB=12米,MA⊥AB于点A,MA=6米,射线BD⊥AB于点B,点P从点B出发沿BA方向往点A运动,每秒走1米,点Q从点B出发沿BD方向运动,每秒走2米,若点P、Q同时从点B出发,出发t秒后,在线段MA上有一点C,使由点C、A、P组成的三角形与△PBQ全等,则t的值是.
三、解答题
-
19.(1)、解分式方程:(2)、化简:20. 已知,如图,在 中,分别在边 上取两点,使得 ,连接 相交于点 ,若
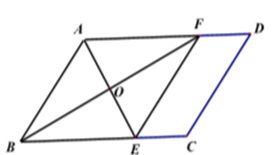 (1)、求证:四边形 是菱形; .(2)、若菱形 的周长为 求 的长.21. 为了让万州区义务教育阶段学生更加深入地了解新型冠状肺炎,从而增强学生的自我防护意识,万州区教委组织了一次新型冠状肺炎相关防疫知识竞赛,通过学校选拔和推荐,对进入此次决赛的小学组和初中组各20名学生的成绩进行了整理和分析,给出了部分信息如下:
(1)、求证:四边形 是菱形; .(2)、若菱形 的周长为 求 的长.21. 为了让万州区义务教育阶段学生更加深入地了解新型冠状肺炎,从而增强学生的自我防护意识,万州区教委组织了一次新型冠状肺炎相关防疫知识竞赛,通过学校选拔和推荐,对进入此次决赛的小学组和初中组各20名学生的成绩进行了整理和分析,给出了部分信息如下:小学组学生决赛成绩统计如下: (满分: 100 分)表1
67
89
88
65
75
76
80
85
88
92
98
100
66
73
86
86
87
95
86
78
初中组学生决赛成绩统计如下: (满分: 100分)表 2
76
83
89
68
68
95
83
86
86
67
77
86
90
84
68
100
86
73
93
86
整理数据:(用 表示学生决赛成绩)表3
分及以上
小学组学生决赛成绩
3
4
9
4
初中组学生决赛成绩
4
3
9
4
分析数据:两组样本数据的平均数、中位数、众数如表所示:表4
平均数
中位数
众数
优秀率(80分及以上)
小学组学生决赛成绩
83
86
初中组学生决赛成绩
(1)、表中 , ;(2)、本次决赛各组分别设一等奖 名,二等奖 名,三等奖 名,在初中的小虎在此次决赛中成绩为 分,他说只要知道一个数据就能确定是否得奖了,你认为他是根据知道的 (填"平均数”、”中位数”、”众数”、"优秀率") ;(3)、根据表4中的数据,你认为哪个组在此次决赛中表现比较好?请说明理由.22. 阅读材料:小学时,我们学习过假分数和带分数的互化.我们可以将一个假分数化为带分数,如:.
初二 (1)班学生小杨同学根据学习分数的方法, 在学习分式这一章时,对分式进行了探究:
根据探究过程,小杨同学说,我可以根据这一探究过程可以分析分式整数解的问题,同学们,你们能吗?
请你帮小杨同学解答下列问题:
(1)、当 为整数时,若 也为整数,求满足条件的所有 的值;(2)、当 为整数时,若 也为整数,求满足条件的所有 的绝对值之和.23. 以诗育德,以诗启智,以诗怡情,以诗塑美,万州区某中学开展诗歌创作比赛,积极营造诗韵书香学生生活.年级决定购买 两种笔记本奖励在此次创作比赛中的优秀学生,已知 种笔记本的单价比 种笔记本的单价便宜 元,已知用1800元购买 种笔记本的数量是用1350元购买 种笔记本的数量的2倍.(1)、求 种笔记本的单价;(2)、根据需要,年级组准备购买 两种笔记本共100本,其中购买 种笔记本的数量不超过 种笔记本的二倍.设购买 种笔记本 本,所需经费为 元,试写出 与 的函数关系式,并请你根据函数关系式求所需的最少经费.24. 函数揭示了两个变量之间的关系,它的表示方法有三种:表格法、图象法、解析式法请你根据学习函数的经验,完成对函数, 的探究.下表是函数 与自变量 的几组对应值:···
-3
-2
-1
0
2
3
4
5
···
···
-0.5
-1
-2
-5
7
4
3
2.5
···
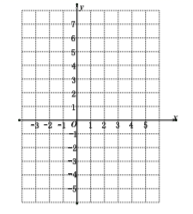 (1)、函数 自变量 的取值范围为(2)、根据表格中的数据,得 , 并在右面平面 直角坐标系 中,画出该函数的图象.(3)、请根据画出的函数图象,直接写出该函数的一条性质:(4)、利用所学函数知识,仔细观察上面表格和函数图象,直接写出不等式 的解集为25. 已知,矩形 在平面直角坐标系中的位置如图所示,点 在 轴的正半轴上,点 在 轴的正半轴上,已知点 的坐标为 , 反比例函数 的图象经过 的中点 ,且与 交于点 ,顺次连接
(1)、函数 自变量 的取值范围为(2)、根据表格中的数据,得 , 并在右面平面 直角坐标系 中,画出该函数的图象.(3)、请根据画出的函数图象,直接写出该函数的一条性质:(4)、利用所学函数知识,仔细观察上面表格和函数图象,直接写出不等式 的解集为25. 已知,矩形 在平面直角坐标系中的位置如图所示,点 在 轴的正半轴上,点 在 轴的正半轴上,已知点 的坐标为 , 反比例函数 的图象经过 的中点 ,且与 交于点 ,顺次连接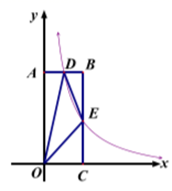 (1)、求线段 的长;(2)、在线段 上存在一点 ,当 的面积等于 时,求点 的坐标;(3)、平面直角坐标系中是否存在一点 ,使得 四点构成平行四边形?若存在,请直接写出 的坐标;若不存在,请说明理由.26. 已知如图1,四边形 是正方形, .
(1)、求线段 的长;(2)、在线段 上存在一点 ,当 的面积等于 时,求点 的坐标;(3)、平面直角坐标系中是否存在一点 ,使得 四点构成平行四边形?若存在,请直接写出 的坐标;若不存在,请说明理由.26. 已知如图1,四边形 是正方形, .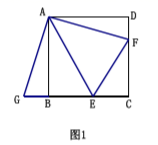 (1)、如图1,若点 分别在边 上,延长线段 至 ,使得 ,若 求 的长;(2)、如图2,若点 分别在边 延长线上时,求证:
(1)、如图1,若点 分别在边 上,延长线段 至 ,使得 ,若 求 的长;(2)、如图2,若点 分别在边 延长线上时,求证: (3)、如图3,如果四边形 不是正方形,但满足 且 ,请你直接写出 的长.
(3)、如图3,如果四边形 不是正方形,但满足 且 ,请你直接写出 的长.