天津市和平区2019-2020学年八年级上学期数学期中试卷
试卷更新日期:2020-09-21 类型:期中考试
一、单选题
-
1. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中具有稳定性的是( )A、
2. 下列图形中具有稳定性的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图,在△ 和△ 中, 90°, .有以下结论:① ;② 平分 ;③ 平分 .其中,正确结论的个数是( )
3. 如图,在△ 和△ 中, 90°, .有以下结论:① ;② 平分 ;③ 平分 .其中,正确结论的个数是( ) A、0 B、1 C、2 D、34. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、0 B、1 C、2 D、34. 如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD5. 等腰三角形一边长等于5,一边长等于9,则它的周长是 ( )
A、14 B、23 C、19或23 D、196. 如图,在△ 中, , 于点 ,若 , ,则△ABC的周长是( ) A、10 B、14 C、16 D、207. 如图,△ 是等边三角形, 为 的中点, ,垂足为点 , ∥ , ,下列结论错误的是( )
A、10 B、14 C、16 D、207. 如图,△ 是等边三角形, 为 的中点, ,垂足为点 , ∥ , ,下列结论错误的是( )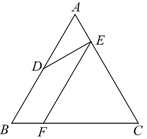 A、 30° B、 C、△ 的周长为10 D、△ 的周长为98. 如图,在四边形 中, , 相交于点 , , , 60°, ,下列结论错误的是( )
A、 30° B、 C、△ 的周长为10 D、△ 的周长为98. 如图,在四边形 中, , 相交于点 , , , 60°, ,下列结论错误的是( ) A、 是△ 的高 B、 30° C、 100° D、9. 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( )
A、 是△ 的高 B、 30° C、 100° D、9. 如图,在△ABC中,AB=AC,∠A=30°,以B为圆心,BC的长为半径圆弧,交AC于点D,连接BD,则∠ABD=( ) A、30° B、45° C、60° D、90°10. 如图,在△ABC中,E , D分别是边AB , AC上的点,且AE=AD , BD , CE交于点F , AF的延长线交BC于点H , 若∠EAF=∠DAF , 则图中的全等三角形共有( )
A、30° B、45° C、60° D、90°10. 如图,在△ABC中,E , D分别是边AB , AC上的点,且AE=AD , BD , CE交于点F , AF的延长线交BC于点H , 若∠EAF=∠DAF , 则图中的全等三角形共有( )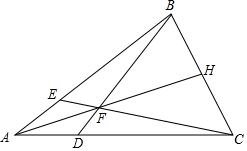 A、4对 B、5对 C、6对 D、7对11. 点(1, )关于直线 的对称点的坐标是( )A、( ,1) B、(-1, ) C、(-1, ) D、( , )12. 如图,过边长为2的等边△ABC的边AB上一点P , 作PE⊥AC于E , Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D , 则DE的长为( )
A、4对 B、5对 C、6对 D、7对11. 点(1, )关于直线 的对称点的坐标是( )A、( ,1) B、(-1, ) C、(-1, ) D、( , )12. 如图,过边长为2的等边△ABC的边AB上一点P , 作PE⊥AC于E , Q为BC延长线上一点,当PA=CQ时,连接PQ交AC边于D , 则DE的长为( )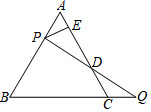 A、 B、1 C、 D、不能确定
A、 B、1 C、 D、不能确定二、填空题
-
13. 如图,点B,E,C,F在一条直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=
 14.
14.如图,点D在△ABC边BC的延长线上,CE平分∠ACD , ∠A=80°,∠B=40°,则∠ACE的大小是度.
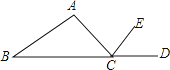 15. 如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是.
15. 如图,AB=AD,∠BAE=∠DAC,要使△ABC≌△ADE,还需添加一个条件,这个条件可以是. 16. 如图,在Rt△ 中, =90°, =30°,在直线 或直线 上取一点 ,使得△ 是等腰三角形,则符合条件的 点有个.
16. 如图,在Rt△ 中, =90°, =30°,在直线 或直线 上取一点 ,使得△ 是等腰三角形,则符合条件的 点有个. 17. 在 中,已知 ,点 分别是边 上的点,且 .则 .
17. 在 中,已知 ,点 分别是边 上的点,且 .则 .三、解答题
-
18. 已知,在四边形ABCD中,∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角,若∠A=α,∠D=β,
 (1)、如图①,当α+β>180°时,∠F=(用含α,β的式子表示);(2)、如图②,当α+β<180°时,请在图②中,画出∠F , 且∠F=(用含α,β的式子表示);(3)、当α,β满足条件时,不存在∠F .19. 如图,点B、F、C、E在一条直线上,AB∥ED , AC∥FD , BF=EC , 求证:△ABC≌△DEF .
(1)、如图①,当α+β>180°时,∠F=(用含α,β的式子表示);(2)、如图②,当α+β<180°时,请在图②中,画出∠F , 且∠F=(用含α,β的式子表示);(3)、当α,β满足条件时,不存在∠F .19. 如图,点B、F、C、E在一条直线上,AB∥ED , AC∥FD , BF=EC , 求证:△ABC≌△DEF . 20. 如图,在△ABC中,∠C=80°,点D在边BC上,且∠ADB=100°,∠BAD= ∠DAC , BE平分∠ABC , 交AD于点E . 求∠BED的大小.
20. 如图,在△ABC中,∠C=80°,点D在边BC上,且∠ADB=100°,∠BAD= ∠DAC , BE平分∠ABC , 交AD于点E . 求∠BED的大小. 21. 如图,在3×3的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中△ 是一个格点三角形.在每张图中画出一个与△ 成轴对称的格点三角形,并将所画三角形涂上阴影.
21. 如图,在3×3的正方形格纸中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形.图中△ 是一个格点三角形.在每张图中画出一个与△ 成轴对称的格点三角形,并将所画三角形涂上阴影. 22. 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
22. 已知,如图,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF. 23. 在△ABC中,DE垂直平分AB , 分别交AB , BC于点D , E , MN垂直平分AC , 分别交AC , BC于点M , N.
23. 在△ABC中,DE垂直平分AB , 分别交AB , BC于点D , E , MN垂直平分AC , 分别交AC , BC于点M , N. (1)、如图①,若∠BAC = 110°,求∠EAN的度数;(2)、如图②,若∠BAC =70°,求∠EAN的度数;(3)、若∠BAC = α(α ≠ 90°),直接写出用α表示∠EAN大小的代数式.24. 如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)、如图①,若∠BAC = 110°,求∠EAN的度数;(2)、如图②,若∠BAC =70°,求∠EAN的度数;(3)、若∠BAC = α(α ≠ 90°),直接写出用α表示∠EAN大小的代数式.24. 如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP). (1)、在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.(2)、将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;(3)、将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
(1)、在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.(2)、将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;(3)、将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.