重庆市涪陵区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-21 类型:期末考试
一、选择题
-
1. 下列各式中是二次根式的是( )A、 B、 C、 D、2. 化简的结果是( )
A、 B、 C、 D、3. 某车间对甲、乙、丙、丁四名工人一天生产出的各自20个零件长度进行调查,每位工人生产的零件长度的平均值均为5厘米,方差分别为S甲2=0.51,S乙2=0.35,S丙2=1.5,S丁2=0.75.其中生产出的零件长度最稳定的工人是( )A、甲 B、乙 C、丙 D、丁4. 下列命题是假命题的是( )A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、对角线互相垂直的四边形是菱形 D、对角线互相垂直平分且相等的四边形是正方形5. 关于函数y=﹣2x+3,下列结论正确的是( )A、y随x的增大而增大 B、图象经过第一、二、三象限 C、图象必经过点(﹣2,3) D、图象与直线y=﹣2x﹣3平行6. 以下列各组数为边长,不能构成直角三角形的是( )A、1, ,2 B、4,5,6 C、5,12,13 D、1,2,7. 如图,在矩形ABCD中,对角线AC、BD相交于点O,∠ABD=60°,则∠BOC的大小为( )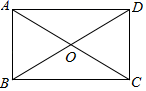 A、30° B、60° C、90° D、120°8. 一次函数y=2x+3与y=3x+2的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 根据如图所示的程序计算函数y的值,若输入x的值是﹣1,则输出y的值是( )
A、30° B、60° C、90° D、120°8. 一次函数y=2x+3与y=3x+2的交点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 根据如图所示的程序计算函数y的值,若输入x的值是﹣1,则输出y的值是( ) A、1 B、3 C、﹣1 D、﹣310. 估计( ) 的值应在( )A、1和2之间 B、3和4之间 C、4和5之间 D、5和6之间11. 若数a使关于x的不等式组 有且只有四个整数解,且关于a的代数式 有意义,则符合条件的所有整数a的和为( )A、﹣3 B、﹣2 C、1 D、212. 如图,在正方形ABCD中,AB=4,E是CD的中点,将 BCE沿BE翻折至 BFE,连接DF,则DF的长度是( )
A、1 B、3 C、﹣1 D、﹣310. 估计( ) 的值应在( )A、1和2之间 B、3和4之间 C、4和5之间 D、5和6之间11. 若数a使关于x的不等式组 有且只有四个整数解,且关于a的代数式 有意义,则符合条件的所有整数a的和为( )A、﹣3 B、﹣2 C、1 D、212. 如图,在正方形ABCD中,AB=4,E是CD的中点,将 BCE沿BE翻折至 BFE,连接DF,则DF的长度是( )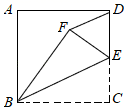 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 如图,在▱ABCD中,对角线AC,BD相交于点O,若AC=10,则AO=.
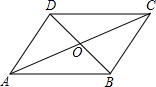 14. 在平面直角坐标系中,直线y=2x+6与x轴的交点坐标是.15. 如图,A、B两地被池塘隔开,在AB外选一点C,连接AC和BC.若E、F分别是AC、BC的中点,EF=50米,则A、B两点的距离为米.
14. 在平面直角坐标系中,直线y=2x+6与x轴的交点坐标是.15. 如图,A、B两地被池塘隔开,在AB外选一点C,连接AC和BC.若E、F分别是AC、BC的中点,EF=50米,则A、B两点的距离为米. 16. 某班体育委员对本班学生一周最炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的平均数是小时.
16. 某班体育委员对本班学生一周最炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的平均数是小时. 17. 《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地四尺.引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有4尺.牵着绳索(绳索头与地面接触)退行,在距木根部8尺处时绳索用尽,问绳索长是多少?根据题意求出绳索长为尺.18. 白鹤公园风景秀丽,成为广大市民休闲锻炼的圣地星期天,小明和爸爸到白鹤公园登山锻炼,他们同时从山脚出发,以各自的速度匀速登山、前20分钟小明以v1的速度一直在前,由于小明体力不支,休息了20分钟,这时他发现爸已超过他走在了前面,小明立即以v2的速度追赶爸爸,直到与爸爸相遇,如图是两人之间相距的路程y(米)与爸爸登山时间x(分)之间的函数图象,则 =.
17. 《九章算术》卷九“勾股”中记载:今有立木,系索其末,委地四尺.引索却行,去本八尺而索尽,问索长几何?译文:今有一竖立着的木柱,在木柱的上端系有绳索,绳索从木柱上端顺木柱下垂后,堆在地面的部分尚有4尺.牵着绳索(绳索头与地面接触)退行,在距木根部8尺处时绳索用尽,问绳索长是多少?根据题意求出绳索长为尺.18. 白鹤公园风景秀丽,成为广大市民休闲锻炼的圣地星期天,小明和爸爸到白鹤公园登山锻炼,他们同时从山脚出发,以各自的速度匀速登山、前20分钟小明以v1的速度一直在前,由于小明体力不支,休息了20分钟,这时他发现爸已超过他走在了前面,小明立即以v2的速度追赶爸爸,直到与爸爸相遇,如图是两人之间相距的路程y(米)与爸爸登山时间x(分)之间的函数图象,则 =. 19. 计算: .
19. 计算: .三、解答题
-
20. 如图,在Rt ABC中,∠ACB=90°,CD是斜边AB上的中线,AC=4,CD=3.求直角边BC的长.
 21. 如图,在四边形ABCD中,O是对角线BD的中点,点E是BC边上一点,连接EO并延长交AD边于点F、交CD延长线于点G.OE=OF,AD=BC.
21. 如图,在四边形ABCD中,O是对角线BD的中点,点E是BC边上一点,连接EO并延长交AD边于点F、交CD延长线于点G.OE=OF,AD=BC. (1)、求证:四边形ABCD是平行四边形;(2)、若∠A=65°,∠G=40°,求∠BEG的度数.22. 某次数学活动时,八年级数学兴趣小组成员研究函数y=|2x﹣4|﹣2的图象和性质.如表是该函数y与自变量x的几组对应值:
(1)、求证:四边形ABCD是平行四边形;(2)、若∠A=65°,∠G=40°,求∠BEG的度数.22. 某次数学活动时,八年级数学兴趣小组成员研究函数y=|2x﹣4|﹣2的图象和性质.如表是该函数y与自变量x的几组对应值:x
……
﹣1
0
1
2
3
4
5
……
y
……
4
2
0
﹣2
0
2
4
……
(1)、如图,在平面直角坐标系xOy中,描出以上各组对应值为坐标的点,再根据描出的点画出该函数的图象; (2)、观察函数图象,当x>2时,y随x的增大而(填“增大”或“减小”);(3)、若一次函数y=kx+b的图象过点A(1,0)、B(4,2),结合你所画的函数图象,不等式kx+b≥|2x﹣4|﹣2的解集是.23. 阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,团结一致、优势互补、取长补短、威力无比.在二次根式中也有这种相辅相成的“对子”.如:( +3)( ﹣3)=﹣4,像( +3)和( ﹣3)这样的两个二次根式,它们的积不含根号,我们就称这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.再如( )与( )也互为有理化因式.于是,下面二次根式除法可以这样运算: = =7+4 .像这样,通过分子、分母同乘以一个式子把分母中的根号化去的过程叫分母有理化.
(2)、观察函数图象,当x>2时,y随x的增大而(填“增大”或“减小”);(3)、若一次函数y=kx+b的图象过点A(1,0)、B(4,2),结合你所画的函数图象,不等式kx+b≥|2x﹣4|﹣2的解集是.23. 阅读材料:黑白双雄,纵横江湖;双剑合壁,天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,团结一致、优势互补、取长补短、威力无比.在二次根式中也有这种相辅相成的“对子”.如:( +3)( ﹣3)=﹣4,像( +3)和( ﹣3)这样的两个二次根式,它们的积不含根号,我们就称这两个二次根式互为有理化因式,其中一个是另一个的有理化因式.再如( )与( )也互为有理化因式.于是,下面二次根式除法可以这样运算: = =7+4 .像这样,通过分子、分母同乘以一个式子把分母中的根号化去的过程叫分母有理化.解决问题:
(1)、2 +3 的一个有理化因式是 , 分母有理化结果是;(2)、计算: + .24. 疫情防控,人人有责.为此某校开展了“新冠疫情”防控知识竞赛现从该校七、八年级中各随机抽取10名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,共分成四组:A.80≤x<85,B.85≤x<90,C.90≤x<95,D.95≤x≤100),下面给出了部分信息:七年级10名学生的竞赛成绩是:99,80,99,86,99,96,90,100,89,82
八年级10名学生的竞赛成绩在C组中的数据是:94,90,94
七八年级抽取的学生竞赛成绩统计表:
年级
平均数
中位数
众数
方差
七年级
92
93
c
52
八年级
92
b
100
50.4

根据以上信息,解答下列问题:
(1)、直接写出上述图表中a、b、c的值:a=、b=、c=.(2)、由以上数据,你认为该校七、八年级中哪个年级学生掌握“新冠疫情”防控知识较好?请说明理由(一条理由即可);(3)、该校七、八年级参加此次竞赛活动的人数分别为1200人和1300人,估计在本次竞赛活动中七、八年级成绩优秀(x≥90)的学生人数共有多少?