辽宁省沈阳市沈河区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-21 类型：期末考试

进入出卷网下载

一、选择题

1. 若x＞y，则下列不等式中成立的是（）

A、x﹣y＜0 B、 $\frac{1}{2}$ x＜ $\frac{1}{2}$ y C、x﹣3＜y﹣3 D、4x＞4y

查看试题解析
2. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则x的值为（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
3. 下面是四个手机APP的图标，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 菱形的两条对角线长分别为6，8，则它的周长是（）

A、5 B、10 C、20 D、24

查看试题解析
5. 下列等式成立的是（）

A、 $\frac{a + 1}{b + 1} = \frac{a}{b}$ B、 $\frac{a - b}{a + b}$ ＝﹣1 C、 $\frac{a^{3}}{b^{3}} = \frac{a}{b}$ D、 $\frac{x^{2} + 2 x y + y^{2}}{x + y}$ ＝x+y

查看试题解析
6. 下列命题中，逆命题是真命题的是（）

A、平行四边形的两组对角分别相等 B、正多边形的每条边都相等 C、成中心对称的两个图形一定全等 D、矩形的两条对角线相等

查看试题解析
7. 下列多项式中，能运用平方差公式分解因式的是（）

A、 $a^{2} + b^{2}$ B、 $2 a - b^{2}$ C、 $a^{2} - b^{2}$ D、 $- a^{2} - b^{2}$

查看试题解析
8. 下列说法不正确的是（）

A、有两组对边分别平行的四边形是平行四边形 B、平行四边形的对角线互相平分 C、平行四边形的对边平行且相等 D、平行四边形的对角互补，邻角相等

查看试题解析
9. 如图，在矩形ABCD中，AB＝8，BC＝4.将矩形沿AC折叠，CD′与AB交于点F，则AF：BF的值为（）

A、2 B、 $\frac{5}{3}$ C、 $\frac{5}{4}$ D、 $\sqrt{3}$

查看试题解析
10. 一次函数y₁＝kx+b与y₂＝x+a的图象如图，则kx+b≥x+a的解集是（）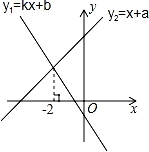

A、x＞﹣2 B、x≥﹣2 C、x≤﹣2 D、无法确定

查看试题解析

二、填空题

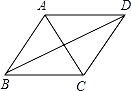
11. 一个n边形的内角和为1080°，则n= ．

查看试题解析
12. 如图，已知四边形ABCD是平行四边形，请你添加一个条件使它成为菱形.这个条件为.

查看试题解析
13. 若分式的 $\frac{3 y}{x - y}$ 的值为5，则x、y扩大2倍后，这个分式的值为.

查看试题解析
14. 如图，点P是∠AOB的角平分线OC上一点，PN⊥OB于点N，点M是线段ON上一点.已知OM＝3，ON＝5，点D为OA上一点，若满足PD＝PM，则OD的长度为.

查看试题解析
15. 如图，点A（2，a）在直线y＝x上，AB⊥x轴于点B，若点C在△AOB的内部，到点O、B的距离相等且CA＝AB，则点C的坐标为.

查看试题解析

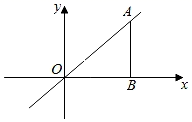
三、解答题

16. 因式分解：

(1)、2a³﹣8a²+8a；

(2)、9x²（9x²﹣2）+1.

查看试题解析
17. 利用数轴解不等式组： ${\begin{array}{l} x - 3 (x - 2) ⩽ 40 \\ \frac{2 x - 1}{3} > x - \frac{5}{6} \end{array}$ .

查看试题解析
18. 先化简，再求值：若x＝3y，求 $\frac{x}{x - y} - \frac{y}{x + y} - \frac{y^{2}}{x^{2} - y^{2}}$ 的值.

查看试题解析
19. 解方程： $\frac{1}{x - 2} - 3 = \frac{x - 1}{2 - x}$ ．

查看试题解析
20. 如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A（1，3），B（2，5），C（4，2）（每个方格的边长均为1个单位长度）

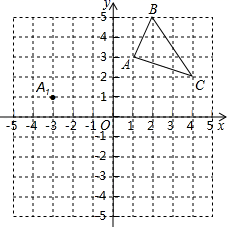
（ 1 ）将△ABC平移，使点A移动到点A₁ ，请画出△A₁B₁C₁；

（ 2 ）作出△ABC关于O点成中心对称的△A₂B₂C₂ ，并直接写出A₂ ， B₂ ， C₂的坐标；

（ 3 ）△A₁B₁C₁与△A₂B₂C₂是否成中心对称？若是，请写出对称中心的坐标；若不是，请说明理由.

查看试题解析
21. 某大型超市从生产基地购进一批水果，运输过程中质量损失10%，假设超市购进这批水果的总量为m千克，每千克进价为n元（不计超市其它费用）.

(1)、如果超市在进价的基础上提高10%作为售价，此时：
①超市最终的销售额为元（用含m、n的代数式表示）；

②在这一次销售中，超市（填：盈利或亏本）.

(2)、如果超市至少要获得17%的利润，请通过计算说明这种水果的售价最低应提高百分之几？

查看试题解析
22. 如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F，AB=10，AC=6，求DF的长.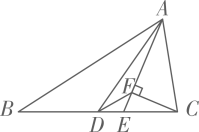

查看试题解析
23. 如图，△ABC中，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连结AD、CE.且AB＝AC.

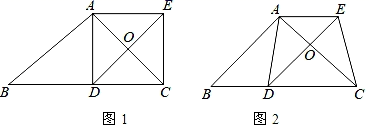(1)、如图1，若D为BC中点时，求证：四边形ADCE是矩形；

(2)、如图2，若D不是BC中点，且∠BAC＝90°，AB＝AC＝10 $\sqrt{2}$ 时，求四边形ADCE的面积.

查看试题解析
24. 如图1，已知AB⊥CD，C是AB上一动点，AB＝CD

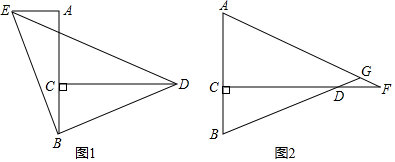(1)、在图1中，将BD绕点B逆时针方向旋转90°到BE，若连接DE，则△DBE为等腰直角三角形；若连接AE，试判断AE与BC的数量和位置关系并证明；

(2)、如图2，F是CD延长线上一点，且DF＝BC，直线AF，BD相交于点G，∠AGB的度数是一个固定值吗？若是，请求出它的度数；若不是，请说明理由．

查看试题解析