辽宁省抚顺市顺城区2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-21 类型:期末考试
一、选择题
-
1. 下列各式中,能与 合并的二次根式是( )A、 B、 C、 D、2. 下列各式中,运算正确的是( )A、 B、 C、 D、3. 下列函数中,正比例函数是( )A、y = B、y = C、y = x+4 D、y = x24. 为了解某校计算机考试情况,抽取了50名学生的计算机考试成绩进行统计,统计结果如表所示,则50名学生计算机考试成绩的众数,中位数分别为( )
考试分数(分)
20
16
12
8
人数
24
18
5
3
A、24,18 B、20,16 C、20,12 D、24,55. 如图,四边形ABCD是菱形,DH⊥AB于点H,若AC=8cm,BD=6cm,则DH=( )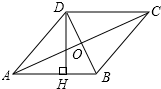 A、5 cm B、 cm C、 cm D、 cm6. 如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )
A、5 cm B、 cm C、 cm D、 cm6. 如图:在△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若CM=5,则CE2+CF2等于( )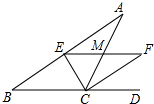 A、75 B、100 C、120 D、1257. 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
A、75 B、100 C、120 D、1257. 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )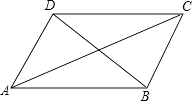 A、①② B、②③ C、①③ D、②④8. 如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )
A、①② B、②③ C、①③ D、②④8. 如图,在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的个数是( )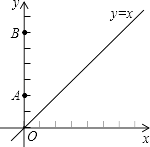 A、2 B、3 C、4 D、59. 如图,在四边形ABCD中,∠A=90°,AB=3, ,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( )
A、2 B、3 C、4 D、59. 如图,在四边形ABCD中,∠A=90°,AB=3, ,点M、N分别为线段BC、AB上的动点,点E、F分别为DM、MN的中点,则EF长度的最大值为( ) A、2 B、3 C、4 D、10. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了32分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米其中正确的结论有( )
A、2 B、3 C、4 D、10. 甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:①甲步行的速度为60米/分;②乙走完全程用了32分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米其中正确的结论有( )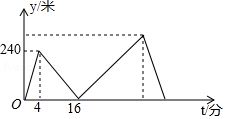 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 若 =x 5,则x的取值范围是 .12. 小张和小李练习射击,两人10次射击训练成绩(环数)的统计结果如表所示,
平均数
中位数
众数
方差
小张
7.2
7.5
7
1.2
小李
7.1
7.5
8
5.4
通常新手的成绩不稳定,根据表格中的信息,估计小张和小李两人中新手是.
13. 某招聘考试分笔试和面试两种,其中笔试按60%、面试按40%计算加权平均数,作为总成绩.孔明笔试成绩90分,面试成绩85分,那么孔明的总成绩是 分.14. 如图,有一块菱形纸片ABCD,沿高DE剪下后拼成一个矩形,矩形的长和宽分别是5cm,3cm.EB的长是. 15. 如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是
15. 如图,在△ABC中,AB=13,BC=12,点D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么CD的长是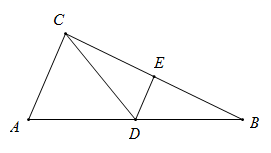 16. 如图,点 是边长为 的菱形 对角线 上的一个动点,点 分别是 边上的中点,则 的最小值是.
16. 如图,点 是边长为 的菱形 对角线 上的一个动点,点 分别是 边上的中点,则 的最小值是. 17. 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为
17. 如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 18. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2…按如图的方式放置,A1 , A2 , A3…和点C1 , C2 , C3…分别在直线y=x+2和x轴上,则点C2020的横坐标是 .
18. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2…按如图的方式放置,A1 , A2 , A3…和点C1 , C2 , C3…分别在直线y=x+2和x轴上,则点C2020的横坐标是 .
三、解答题
-
19. 计算:(1)、 6 +(2)、( )2+2 ×320. 某校全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况,并统计绘制成了如图两幅不完整的条形统计图和扇形统计图,请根据所提供的信息,解答下列问题:
 (1)、本次共抽查学生 ▲ 人,并将条形图补充完整:(2)、捐款金额的众数是元,中位数是元;(3)、若该校共有2000名学生参加捐款,根据样本平均数估计该校大约可捐款多少元?21. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动.
(1)、本次共抽查学生 ▲ 人,并将条形图补充完整:(2)、捐款金额的众数是元,中位数是元;(3)、若该校共有2000名学生参加捐款,根据样本平均数估计该校大约可捐款多少元?21. 如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点N沿路线O→A→C运动. (1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、当△ONC的面积是△OAC面积的 时,求出这时点N的坐标.22. 如图,直线y1=2x 2 的图像与y轴交于点A,直线y2= 2x+6的图像与y轴交于点B,两者相交于点C.
(1)、求直线AB的解析式.(2)、求△OAC的面积.(3)、当△ONC的面积是△OAC面积的 时,求出这时点N的坐标.22. 如图,直线y1=2x 2 的图像与y轴交于点A,直线y2= 2x+6的图像与y轴交于点B,两者相交于点C.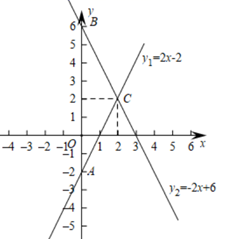 (1)、方程组 的解是:(2)、当y1>0与y2>0同时成立时,x的取值范围为:(3)、点M是直线y1=2x 2上的动点,过点M作MN⊥x轴,交直线y2= 2x+6于点N,当MN≤8时,设点M的横坐标为m,则求出m的取值范围.23. 如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.
(1)、方程组 的解是:(2)、当y1>0与y2>0同时成立时,x的取值范围为:(3)、点M是直线y1=2x 2上的动点,过点M作MN⊥x轴,交直线y2= 2x+6于点N,当MN≤8时,设点M的横坐标为m,则求出m的取值范围.23. 如图,菱形ABCD的对角线AC、BD相交于点O,BE∥AC,AE∥BD,OE与AB交于点F.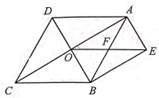 (1)、试判断四边形AEBO的形状,并说明理由;(2)、若OE=10,AC=16,求菱形ABCD的面积.24. 如图,正方形ABCD的对角线交于点O , 点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M , OF、AB的延长线交于点N , 连接MN .
(1)、试判断四边形AEBO的形状,并说明理由;(2)、若OE=10,AC=16,求菱形ABCD的面积.24. 如图,正方形ABCD的对角线交于点O , 点E、F分别在AB、BC上(AE<BE),且∠EOF=90°,OE、DA的延长线交于点M , OF、AB的延长线交于点N , 连接MN . (1)、求证:OM=ON;(2)、若正方形ABCD的边长为6,OE=EM , 求MN的长.25. 小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系式如图2所示.
(1)、求证:OM=ON;(2)、若正方形ABCD的边长为6,OE=EM , 求MN的长.25. 小明家今年种植的“红灯”樱桃喜获丰收,采摘上市20天全部销售完,小明对销售情况进行跟踪记录,并将记录情况绘成图象,日销售量y(单位:千克)与上市时间x(单位:天)的函数关系如图1所示,樱桃价格z(单位:元/千克)与上市时间x(单位:天)的函数关系式如图2所示. (1)、观察图象,直接写出日销售量的最大值;(2)、求小明家樱桃的日销售量y与上市时间x的函数解析式;(3)、试比较第10天与第12天的销售金额哪天多?26. 如图,△ABC为等腰直角三角形,∠ACB=90°,D,E分别是AC、AB的中点,P为直线DE上的一点,PQ⊥PC交直线AB于Q.
(1)、观察图象,直接写出日销售量的最大值;(2)、求小明家樱桃的日销售量y与上市时间x的函数解析式;(3)、试比较第10天与第12天的销售金额哪天多?26. 如图,△ABC为等腰直角三角形,∠ACB=90°,D,E分别是AC、AB的中点,P为直线DE上的一点,PQ⊥PC交直线AB于Q. (1)、如图1,当P在ED延长线上时,求证:EC+EQ= EP;(2)、当P在射线DE上时,请直接写出EC,EQ,EP三条线段之间的数量关系.
(1)、如图1,当P在ED延长线上时,求证:EC+EQ= EP;(2)、当P在射线DE上时,请直接写出EC,EQ,EP三条线段之间的数量关系.