江苏省徐州市2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-21 类型:期末考试
一、选择题
-
1. 在以下标志中,是中心对称图形的是( )A、
 绿色食品
B、
绿色食品
B、 响应环保
C、
响应环保
C、 可回收物
D、
可回收物
D、 节水
2. 下列调查中,适宜采用普查方式的是( )A、调查一批节能灯管的使用寿命 B、了解全国八年级学生身高的现状 C、检查一枚用于发射卫星的运载火箭的各零部件 D、考察人们保护海洋的意识3. 下列运算正确的是( )A、 + = B、 =2 C、 • = D、 ÷ =24. 菱形具有,而矩形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相垂直5. 下列分式是最简分式的是( )A、 B、 C、 D、6. 下列事件中,属于必然事件的是( )A、随时打开电视机,正在播新闻 B、优秀射击运动员射击一次,命中靶心 C、抛掷一枚质地均匀的骰子,出现4点朝上 D、长度分别是3cm,5cm,6cm的三根木条首尾相接,组成一个三角形7. 某公司某年产量变化如图所示.下列说法正确的是( )
节水
2. 下列调查中,适宜采用普查方式的是( )A、调查一批节能灯管的使用寿命 B、了解全国八年级学生身高的现状 C、检查一枚用于发射卫星的运载火箭的各零部件 D、考察人们保护海洋的意识3. 下列运算正确的是( )A、 + = B、 =2 C、 • = D、 ÷ =24. 菱形具有,而矩形不一定具有的性质是( )A、对边相等 B、对角相等 C、对角线相等 D、对角线互相垂直5. 下列分式是最简分式的是( )A、 B、 C、 D、6. 下列事件中,属于必然事件的是( )A、随时打开电视机,正在播新闻 B、优秀射击运动员射击一次,命中靶心 C、抛掷一枚质地均匀的骰子,出现4点朝上 D、长度分别是3cm,5cm,6cm的三根木条首尾相接,组成一个三角形7. 某公司某年产量变化如图所示.下列说法正确的是( )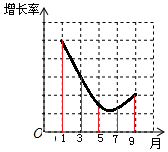 A、1—5月产量逐渐下降 B、1—9月每月生产量不断增加 C、1月份产量最大 D、1—9月月产量有增加有减少8. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=A2019A2020 , 过点A1、A2、A3、…、A2019、A2020分别作x轴的垂线,与反比例函数 的图像依次相交于P1、P2、P3、…P2019、P2020 , 得到直角三角形OP1A1、A1P1A2、…、A2019P2020A2020 , 并设其面积分别为S1、S2、…、S2020 , 则S2020的值为( )
A、1—5月产量逐渐下降 B、1—9月每月生产量不断增加 C、1月份产量最大 D、1—9月月产量有增加有减少8. 如图,在x轴正半轴上依次截取OA1=A1A2=A2A3=…=A2019A2020 , 过点A1、A2、A3、…、A2019、A2020分别作x轴的垂线,与反比例函数 的图像依次相交于P1、P2、P3、…P2019、P2020 , 得到直角三角形OP1A1、A1P1A2、…、A2019P2020A2020 , 并设其面积分别为S1、S2、…、S2020 , 则S2020的值为( )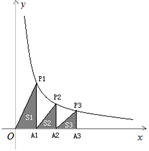 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 化简: =; × = .10. 计算: =.11. 若代数式 有意义,则实数x的取值范围是 .12. 已知菱形ABCD的面积是12cm2 , 对角线AC=4cm,则菱形的边长是cm.13. 已知一个样本中,样本容量为50,这50个数据分别落在5个小组内,第一、二、四、五小组的频数分别是2,10,10,20,则第三个小组的频率为.14. 如图,正比例函数 的图象与反比例函数 的图象相交于A,B两点,其中点B的横坐标为-2,当y1<y2时,x的取值范围是.
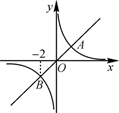 15. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为.
15. 如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别为6、7、8,四边形DHOG面积为.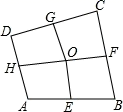 16. 一副直角三角板叠放如图所示,现将含 角的三角板固定不动,把含 角的三角板绕直角顶点沿逆时针方向以 的速度匀速旋转一周,当两块三角板的斜边平行时,则三角板旋转运动的时间为.
16. 一副直角三角板叠放如图所示,现将含 角的三角板固定不动,把含 角的三角板绕直角顶点沿逆时针方向以 的速度匀速旋转一周,当两块三角板的斜边平行时,则三角板旋转运动的时间为.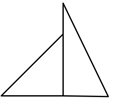
三、解答题
-
17. 计算:(1)、 ;(2)、 .18.(1)、化简: ;(2)、解方程: .19. 家庭过期药品属于“有害垃圾”,处理不当将污染环境,危害健康.某校甲、乙两位同学为了解全市家庭处理过期药品的方式,进行了一次抽样调查,结果如下(大写英文字母A—F分别代表不同的处理方式):

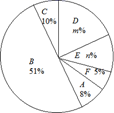 (1)、m= , n=;(2)、补全条形统计图;(3)、若该市有180万户家庭,试估计全市用E方式处理过期药品的家庭数量.20. 已知△ABC的顶点A、B、C在边长为1的网格格点上.
(1)、m= , n=;(2)、补全条形统计图;(3)、若该市有180万户家庭,试估计全市用E方式处理过期药品的家庭数量.20. 已知△ABC的顶点A、B、C在边长为1的网格格点上.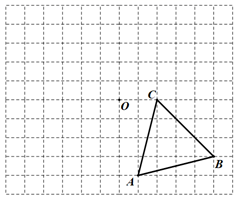 (1)、①画△ABC绕点O逆时针旋转90°得到的△A1B1C1;
(1)、①画△ABC绕点O逆时针旋转90°得到的△A1B1C1;②画△A1B1C1关于点O的中心对称图形△A2B2C2;
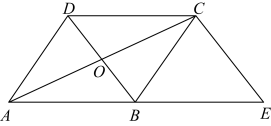
(2)、平行四边形A1B1A2B2的面积为 .21. 如图,已知菱形ABCD的对角线相交于点O , 延长AB至点E , 使BE=AB , 连接CE . ∠E=50°,求∠BAO的大小.
 22. 科技创新加速中国高铁技术发展,某建筑集团承担一座高架桥的铺设任务,在合同期内高效完成了任务,这是记者与该集团工程师的一段对话:
22. 科技创新加速中国高铁技术发展,某建筑集团承担一座高架桥的铺设任务,在合同期内高效完成了任务,这是记者与该集团工程师的一段对话:记者:你们是用9天完成4800米长的高架桥铺设任务的?
工程师:是的,我们铺设600米后,采用新的铺设技术,这样每天铺设长度是原来的2倍.
通过这段对话,请你求出该建筑集团原来每天铺设高架桥的长度.
23. 某气象研究中心观测到一场沙尘暴从发生到减弱的过程,开始一段时间风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,然后风速不变,当沙尘暴遇到绿色植被区时,风速y(千米/小时),时间x(小时)成反比例关系地慢慢减弱,结合风速与时间的图象,回答下列问题: (1)、这场沙尘暴的最高风速是多少?最高风速维持了多长时间;(2)、求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?(3)、在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?
(1)、这场沙尘暴的最高风速是多少?最高风速维持了多长时间;(2)、求出当x≥20时,风速y(千米/小时)与时间x(小时)之间的函数关系?(3)、在这次沙尘暴的形成过程中,当风速不超过10千米/小时称为“安全时刻”,其余时刻是“危险时刻”.问这次风暴的整个过程中,“危险时刻”一共有多长时间?

