北京市海淀区理工大学附中2019-2020学年八年级上学期数学期中试卷
试卷更新日期：2020-09-21 类型：期中考试
一、单选题
-
1. 下列图形中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列运算的结果为a6的是（ ）A、 B、 C、 D、3. 如果关于x的多项式（2x-m）与(x+5)的乘积中，常数项为15，则m的值为（ ）A、3 B、－3 C、10 D、－104. 如图，△ABC中，D、E两点分别在AC、BC上，AB＝AC，CD＝DE，若∠A＝40°，∠ABD：∠DBC＝3：4，则∠BDE＝（ ）
A、24° B、25° C、30° D、35°5. 若a，b，c是三角形的三边，则代数式（a-b）2-c2的值是（ ）A、正数 B、负数 C、等于零 D、不能确定6. 如图，D是AB边上的中点，将△ABC沿过D的直线折叠，使点A落在BC上F处，若∠B=50°，则∠EDF的度数为 （ ）
A、50° B、40° C、80° D、60°7. 如图，在△ABE中，∠BAE＝105°，AE的垂直平分线MN交BE于点C，且AB＝CE，则∠B的度数是（ ）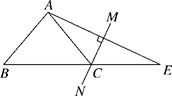
A、45° B、60° C、50° D、55°8. 如图，四边形ABCD 中，AB=AD ， 点B关于AC的对称点B′恰好落在CD上，若∠BAD= ，则∠ACB的度数为（ ）
A、 α B、90°- α C、45° D、α-45°二、填空题
-
9. 若等腰三角形的顶角为 ，则这个等腰三角形的底角的度数 ．10. 对于任意实数，规定 =ad－bc.则当2x2－6x+2=0时， =.11. 如图，在△ABC中，AB=AC，D，E，F分别在BC，AC，AB上的点，且BF=CD，BD=CE，∠FDE=α，则∠A的度数是度．（用含α的代数式表示）
12. 如图，△ABC中，H是高AD、BE的交点，且BH＝AC，则∠ABC＝.
13. 如图，在△ABC中， ，AB垂直平分线DE交AB边于点D，交BC边于点E，在线段DE上有一动点P，连接AP、PC，则△APC的周长最小值为 ．
14. 已知等腰三角形一腰上的高与另一腰的夹角为35°，则这个等腰三角形顶角的度数为.15. 已知三角形的两边长分别为5和7，则第三边 的取值范围是.16. 如图，已知BD⊥AE于点B，DC⊥AF于点C，且DB=DC，∠BAC=40°，∠ADG=130°，则∠DGF=.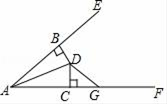
三、解答题
-
17. 计算下列各题：(1)、3x•6x2y(2)、（a+2b）（a﹣2b）18. 如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C，AF与DE相交于点O，请判断△OEF的形状，并说明理由.
19. 先化简，再求值：（x+3）（x﹣3）-（-2x+1）（x﹣3）﹣4x（x﹣1），其中x＝4.20. 已知x7=2,y9=3,试比较x与y的大小.21. 计算：（8x2y﹣4x4y3）÷（﹣2x2y）22. 已知：如图，点A、E、F、C在同一条直线上，DF＝BE，∠B＝∠D，AD∥BC，求证：AE＝CF.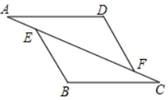
23. 已知，如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD．
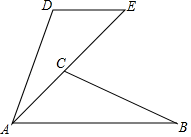24. 已知：如图，AC=BD，AD⊥AC，BC⊥BD．求证：AD=BC
25. 已知：如图，点B、C、E三点在同一条直线上， CD平分∠ACE， DB=DA，DM⊥BE于M.
(1)、求证：AC=BM+CM；(2)、若AC=2，BC=1，求CM的长.26. 如图，已知：线段AB．
(1)、尺规作图：作线段AB的垂直平分线l，与线段AB交于点D；（保留作图痕迹，不写作法）(2)、在（1）的基础上，点C为l上一个动点(点C不与点D重合)，连接CB，过点A作AE⊥BC，垂足为点E．①当垂足E在线段BC上时，直接写出∠ABC度数的取值范围是；
②请你画出一个垂足E在线段BC延长线上时的图形，并求证∠BAE=∠BCD．
27. 已知，如图：AD是△ABC的中线，AE⊥AB，AE=AB，AF⊥AC，AF=AC，连结EF．试猜想线段AD与EF的关系，并证明
28. 定义：如图1，在△ABC和△ADE中，AB=AC=AD=AE，当∠BAC+∠DAE=180° 时，我们称△ABC与△DAE互为“顶补等腰三角形”，△ABC的边BC上的高线AM叫做△ADE的“顶心距”，点A叫做“旋补中心”.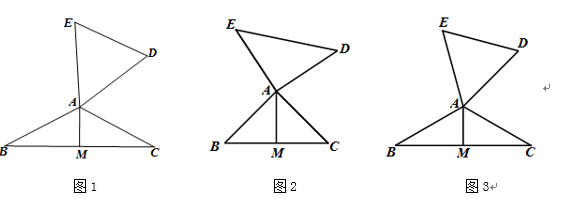
(1)、特例感知：在图2，图3中，△ABC与△DAE互为“顶补等腰三角形”，AM是“顶心距”.①如图2，当∠BAC=90°时，AM与DE之间的数量关系为AM=DE；
②如图3，当∠BAC=120°，ED=6时，AM的长为.
(2)、猜想论证：在图1中，当∠BAC为任意角时，猜想AM与DE之间的数量关系，并给予证明.
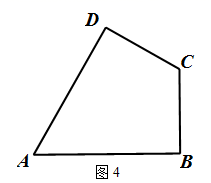
(3)、拓展应用如图4，在四边形ABCD中，AD=AB，CD=BC，∠B=90°，∠A=60°，CA= ，在四边ABCD的内部找到点P，使得△PAD与△PBC互为“顶补等腰三角形”.并回答下列问题.
①请在图中标出点P的位置，并描述出该点的位置为；
②直接写出△PBC的“顶心距”的长为.
