江苏省苏州市姑苏区六校联考2019-2020学年八年级下学期数学期末考试试卷
试卷更新日期:2020-09-21 类型:期末考试
一、选择题
-
1. 下列调查中,适合采用普查的是( )A、全班学生周六晚上收看“新闻联播”的次数 B、某品牌灯泡的使用寿命 C、长江中现有鱼的科类 D、公民垃圾分类的意识2. 若二次根式 有意义,则x的取值范围是( )A、x<2 B、x≠2 C、x≤2 D、x≥23. 一只不透明的袋子中装有一些红球和白球,这些球除颜色外都相同.将球摇匀,从中任意摸出一个球,摸到红球是( )A、确定事件 B、必然事件 C、不可能事件 D、随机事件4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、正三角形 B、正方形 C、等腰三角形 D、平行四边形5. 若反比例函数的图象经过点(-2,3),则该反比例函数图象一定经过点( )A、(2,-3) B、(-2,-3) C、(2,3) D、(-1,-6)6. 若分式方程 有增根,则a的值是( )A、4 B、3 C、2 D、17. 下列说法正确的是( ).A、对角线相等的平行四边形是菱形 B、有一组邻边相等的平行四边形是菱形 C、对角线相互垂直的四边形是菱形 D、有一个角是直角的平行四边形是菱形8. 如图,直线y=-x+3与y轴交于点A,与反比例函数y= (k≠0)的图象交于点C,过点C作CB⊥x轴于点B,AO=3BO,则反比例函数的解析式为( )
 A、y= B、y=- C、y= D、y=-9. 如图,将△ABC绕顶点A顺时针旋转60°后,得到△AB'C',且C'为BC的中点,则C'D:DB'=( )
A、y= B、y=- C、y= D、y=-9. 如图,将△ABC绕顶点A顺时针旋转60°后,得到△AB'C',且C'为BC的中点,则C'D:DB'=( )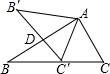 A、 B、 C、 D、10. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A、 B、 C、 D、10. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )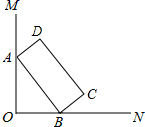 A、 B、 C、 5 D、
A、 B、 C、 5 D、二、填空题
-
11. 当x时, 分式 有意义.12. 已知点A1(-1,y1),A2(-3,y2)都在反比例函数y= (k>0)的图像上,则y1与y2的大小关系为.13. 如果 = 0, 则 =.14. 一组数据共有100个,分成四组后其中前三组的频率分别是0.14,0.20,0.36.则第四组数据的个数为.15. 点A(a,b)是一次函数y=x﹣2与反比例函数y= 的交点,则a2b﹣ab2= .16. 甲,乙两个机器人检测零件,甲比乙每小时多检测10个,甲检测300个与乙检测200个所用时间相等.若设乙机器人每小时检则零件x个,依题意列分式方程为.17. 如图,△ABC的周长为19, 点D、E在边BC上,∠ABC的平分线垂直于AE,垂足为N ,∠ACB的平分线重直于AD,垂足为M,若BC=7,则MN的长度为.
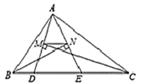 18. 如图,在平行四边形ABCD中,AD=2AB.F是AD的中点,作CE⊥AB, 垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF+ ∠D=90°;(2)∠AEF+∠ECF=90°;(3) =2 ; (4)若∠B=80 ,则∠AEF=50°.其中一定成立的是 (把所有正确结论的字号都填在横线上).
18. 如图,在平行四边形ABCD中,AD=2AB.F是AD的中点,作CE⊥AB, 垂足E在线段AB上,连接EF、CF,则下列结论:(1)∠DCF+ ∠D=90°;(2)∠AEF+∠ECF=90°;(3) =2 ; (4)若∠B=80 ,则∠AEF=50°.其中一定成立的是 (把所有正确结论的字号都填在横线上).
三、解答题
-
19. 计算:(1)、 ;(2)、20. 解分式方程: ﹣1= .21. 先化简,再求值: [其中, ]22. 已知, a= ,b= ,求值:(1)、ab;(2)、a2- 3ab+b2.23. 某校音乐组决定围绕在“舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项) ”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制如下两幅不完整的统计图.
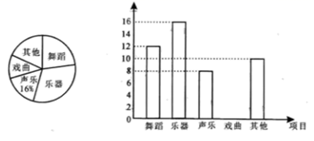
请你根据统计图解答下列问题.
(1)、在这次调查中,一共抽查了名学生,其中喜欢舞蹈活动项目的人数占抽查总人数的百分比为;(2)、请你补全条形统计图;(3)、某班7位同学中,1人喜欢舞蹈,2人喜欢乐器,1人喜欢声乐,3人喜欢乐曲,老师要从这7人中任选1人参加学校社团展演,则恰好选出1人喜欢乐器的概率是.24. 如图在平面直角坐标系xOy中,函数 ( )的图象与一次函数 的图象的交点为A(m,2). (1)、求一次函数的解析式;(2)、观察图像直接写出使得 的 的取值范围;
(1)、求一次函数的解析式;(2)、观察图像直接写出使得 的 的取值范围;
(3)、设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,直接写出P点的坐标.
25. 如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.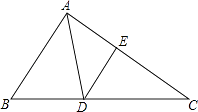 (1)、求证:△DCE∽△BCA;(2)、若AB=3,AC=4.求DE的长.26. 在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.
(1)、求证:△DCE∽△BCA;(2)、若AB=3,AC=4.求DE的长.26. 在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接AE、AF、CE、CF,如图所示.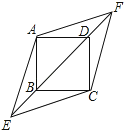 (1)、求证:△ABE≌△ADF;(2)、试判断四边形AECF的形状,并说明理由.27. [探索规律]
(1)、求证:△ABE≌△ADF;(2)、试判断四边形AECF的形状,并说明理由.27. [探索规律]如图①,在△ABC中,点D、E、F分别在AB、 BC、 AC上,且DF//BC,EF//AB.设△ADF的边DF上的高为h1 , △EFC的边CE上的高为h2.
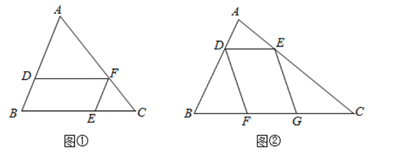 (1)、若△ADF、△EFC的面积分别为4和1,则 =;(2)、某校数学兴趣小组的同学对△ADF、△EFC、四边形BDEF的面积关系进行了研究设△ADF、△EFC、四边形BDEF的面积分别为S1、 S2、S, EC的长为a,则S2= (用含a和h2的式子表示);S1= (用含a、h1和h2的式子表示);S=(用含a、h1的式子表示);从而得出S=2 .(3)、[解决问题]
(1)、若△ADF、△EFC的面积分别为4和1,则 =;(2)、某校数学兴趣小组的同学对△ADF、△EFC、四边形BDEF的面积关系进行了研究设△ADF、△EFC、四边形BDEF的面积分别为S1、 S2、S, EC的长为a,则S2= (用含a和h2的式子表示);S1= (用含a、h1和h2的式子表示);S=(用含a、h1的式子表示);从而得出S=2 .(3)、[解决问题]如图②,在△ABC中,点D、E分别在AB、AC上,点F、G在BC上,且DE//BC,DF//EG.若△ADE、△DBF.△EGC的面积分别为2、3、 5,求△ABC的面积.
28. 如图①,在矩形ABCD中,点P从AB边的中点E出发沿着E-B-C匀速运动,速度为每秒1个单位长度,到达点C后停止运动,点Q是AD上的点AQ=5,设△PAQ的面积为y,点P运动的时间为t秒,y 与t的函数关系如图②所示.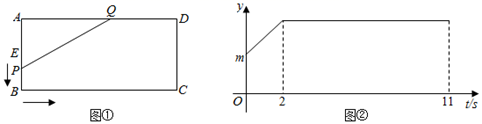 (1)、图①中AB= , BC= , 图②中m=.(2)、点P在运动过程中,将矩形沿PQ所在直线折叠,则t为何值时,折叠后顶点A的对应点A'落在矩形的一边上.
(1)、图①中AB= , BC= , 图②中m=.(2)、点P在运动过程中,将矩形沿PQ所在直线折叠,则t为何值时,折叠后顶点A的对应点A'落在矩形的一边上.