江苏省南京市玄武区2019-2020学年八年级下学期数学期末考试试卷

试卷更新日期：2020-09-21 类型：期末考试

进入出卷网下载

一、选择题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 在一个不透明的盒子里装有3个红球和2个白球，每个球除颜色外都相同，从中任意摸出3个球.下列事件中，不可能事件是（）

A、摸出的3个球都是红球 B、摸出的3个球都是白球 C、摸出的3个球中有2个红球1个白球 D、摸出的3个球中有2个白球1个红球

查看试题解析
3. 下列运算中，正确的是（）

A、 $\frac{1}{- x - y} = - \frac{1}{x - y}$ B、 $\frac{3 x + y}{2 x + y} = \frac{3}{2}$ C、 $\frac{x^{2} + y^{2}}{x + y} = x + y$ D、 $\frac{y - x}{x^{2} - y^{2}} = - \frac{1}{x + y}$

查看试题解析
4. 下列说法正确的是（）

A、一组对边平行，另一组对边相等的四边形是平行四边形 B、对角线相等的四边形是矩形 C、每一条对角线都平分一组对角的四边形是菱形 D、对角线互相垂直且相等的四边形是正方形

查看试题解析
5. 如图，点A在反比例函数y＝ $\frac{k}{x}$ （x＞0）的图像上，C是y轴上一点，过点A作AB⊥x轴，垂足为B，连接AC、BC.若△ABC的面积为3，则k的值为（）

A、9 B、6 C、3 D、1.5

查看试题解析
6. 如图，在矩形ABCD中，AB＝5，BC＝6，点E在BC边上，且BE＝2，F为AB边上的一个动点，连接EF，以EF为边作等边△EFG，且点G在矩形ABCD内，连接CG，则CG的最小值为（）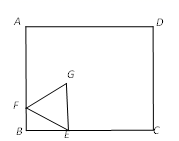

A、3 B、2.5 C、4 D、2 $\sqrt{3}$

查看试题解析

二、填空题

7. 若代数式 $\sqrt{x - 1}$ 在实数范围内有意义，则x的取值范围是。

查看试题解析
8. 若分式 $\frac{x^{2} - 4}{x - 2}$ 的值为0，则 $x$ 的值是.

查看试题解析
9. 计算 $\sqrt{2 a}$ · $\sqrt{8 a}$ (a≥0)的结果是.

查看试题解析

10. 一个不透明的袋子中装有若干个除颜色外都相同的小球，小明每次从袋子中随机摸出一个球，记录下颜色，然后放回，重复这样的试验3000次，记录结果如下：

实验次数n	100	200	300	500	800	1000	2000	3000
摸到红球次数m	65	124	178	302	481	620	1240	1845
摸到红球频率 $\frac{m}{n}$	0.65	0.62	0.593	0.604	0.601	0.620	0.620	0.615

估计从袋子中随机摸出一个球恰好是红球的概率约为.（精确到0.1）

查看试题解析

11. 用配方法解一元二次方程x²＋6x＋1＝0时，配方后方程可化为：.

查看试题解析
12. 已知点A（－1，y₁）、B（2，y₂）在反比例函数y＝ $\frac{m - 1}{x}$ 的图像上，且y₁＞y₂ ，则m的取值范围是.

查看试题解析
13. 如图，顺次连接菱形ABCD的各边中点E、F、G、H.若AC=a，BD=b，则四边形EFGH的面积是.

查看试题解析
14. 已知一次函数y₁＝k₁x＋b（k₁ ， b为常数）与反比例函数y₂＝ $\frac{k_{2}}{x}$ （k₂为常数），函数y₁、y₂与自变量x的部分对应值分别如表1、表2所示：

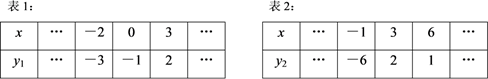
则关于x的不等式k₁x＋b＜ $\frac{k_{2}}{x}$ 的解集是.

查看试题解析
15. 如图，菱形纸片ABCD，AB＝4，∠B＝60°，将该菱形纸片折叠，使点B恰好落在CD边的中点B′处，折痕与边BC、BA分别交于点M、N.则BM的长为.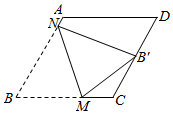

查看试题解析
16. 如图，将边长为2的正方形 ABCD 绕点A按逆时针方向旋转，得到正方形AB'C'D'，连接BB'、BC'，在旋转角从0°到180°的整个旋转过程中，当BB'＝BC'时，△BB'C'的面积为.

查看试题解析

三、解答题

17. 计算：

(1)、 $\frac{1}{\sqrt{3}} + 3 \sqrt{12} - \sqrt{48}$ ；

(2)、 $\frac{\sqrt{5} + \sqrt{20}}{\sqrt{5}} - \sqrt{\frac{1}{3}} \times \sqrt{12}$ .

查看试题解析
18. 解分式方程：

(1)、 $\frac{5 x + 2}{x^{2} + x} = \frac{3}{x + 1}$ ；

(2)、 $\frac{x}{x - 1} = \frac{3}{2 x - 2} - 2$ .

查看试题解析
19. 解一元二次方程：

(1)、x²＋2x－1＝0；

(2)、(x－3)²＝2x－6.

查看试题解析
20. 先化简,再求值： $(x + \frac{1}{x - 2}) \div (1 + \frac{1}{x - 2})$ ，其中x＝－ $\frac{1}{2}$ .

查看试题解析
21. 某中学图书馆将全部图书分为自然科学、文学艺术、社会百科、哲学等四个类别.为了了解图书的借阅情况，图书管理员随机抽取了某月图书的借阅情况进行统计，并绘制成如下尚不完整的统计表和统计图.

(1)、该月四类图书的借阅册数一共是册，其中“自然科学”类所占的百分比是；

(2)、补全条形统计图，并算出扇形统计图中“哲学”对应扇形的圆心角度数为°；

(3)、若该中学打算购买四类图书共10000册，根据上述信息，请你估算“哲学”类图书应购买多少册？

查看试题解析
22. 一辆货车和一辆轿车从南京出发，均沿沪宁高速公路匀速驶向目的地上海.已知沪宁高速公路全长约300 km.设货车的速度是x km / h，到达上海所用的时间为y h.

(1)、写出y关于x的函数表达式；

(2)、沪宁高速公路规定：货车的速度不得超过90 km / h.求货车到达上海所需的最短时间；

(3)、若轿车的速度是货车的1.5倍，轿车到达上海所用的时间比货车少1小时15分钟，求轿车的速度.

查看试题解析
23. 如图，在▱ABCD中，将对角线BD分别向两个方向延长至点E、F，且 BE＝DF.连接AF、CF、CE、AE.

(1)、求证：四边形AECF是平行四边形；

(2)、若AD＝4，BE＝3，∠ADB＝∠CBD＝90°，当四边形AECF是矩形时，则BD的长为.

查看试题解析
24. 已知关于x的一元二次方程(x－m)²＋2(x－m)＝0（m为常数）.

(1)、求证：不论m为何值，该方程总有两个不相等的实数根.

(2)、若该方程有一个根为4，求m的值.

查看试题解析
25. 如图，在下列方格纸中，A、B是两个格点，请用无刻度的直尺在方格纸中完成下列画图.（不写画法，保留画图痕迹）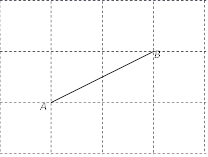

（ 1 ）画出一个∠ABC，使得∠ABC＝45°；

（ 2 ）画出线段AB的垂直平分线.

查看试题解析
26.

(1)、如图①，在菱形ABCD中，P、Q分别是边BC、CD上的点，连接AP、AQ，且∠PAQ＝∠B.求证：AP＝AQ.

下面是小文对这道试题的思考，先研究特殊情况，再证明一般情况.

（Ⅰ）如图②，当AP⊥BC于点P时，请在下列框图中补全他的证明思路.

（Ⅱ）如图①，当AP与BC不垂直时，……请你完成证明.

小文完成证明后，又进一步思考，提出下列问题，请你完成解答.

(2)、如图③，在菱形ABCD中，P、Q分别是BC、CD延长线上的点，且∠PAQ＝∠B.若AB＝4，∠B＝60°，∠APB＝45°，则四边形ABCQ的面积是 .

查看试题解析
27. 在平面直角坐标系中，P是平面内任意一点（坐标轴上的点除外），过点P分别作x轴，y轴的垂线，如果由点P、原点、两个垂足这4个点为顶点的矩形的周长与面积相等，那么称这个点P是平面直角坐标系中的“奇点”.例如：如图①，过点P（4，4）分别作x轴，y轴的垂线，垂足分别为A，B，矩形OAPB的周长为16，面积也为16，周长与面积相等，所以点P是奇点.请根据以上材料回答下列问题：

(1)、已知点C（2，2）、D（－4，－4）、E（ $\frac{10}{3}$ ，－5），其中是平面直角坐标系中的奇点的有；（填字母代号）

(2)、我们可以从函数的角度研究奇点.已知点P（x，y）是第一象限内的奇点.
I.求y关于x的函数表达式，并写出自变量x的取值范围；

II.借鉴研究一次函数和反比例函数的经验，类似地可以对I中所求出的函数的图象和性质进行探索，下列结论正确的是 ▲ （填写所有正确的序号）；

①图像与坐标轴没有交点

②在第一象限内，y随着x的增大而减小

③对于图像上任意一点（x，y），（x－2）·（y－2）是一个定值

(3)、在第一象限内，直线y＝kx＋8（k为常数）上奇点的个数随着k的值变化而变化，直接写出奇点的个数及对应的k的取值范围.

查看试题解析