四川省遂宁市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-21 类型:期末考试
一、单选题
-
1. 已知关于x的方程3x﹣m+4=0的解是x=﹣2,则m的值为( )A、2 B、﹣2 C、4 D、52. 下列等式变形正确的是( )A、若﹣2x=5,则x= B、若3(x+1)﹣2x=1,则3x+1﹣2x=1 C、若5x﹣6=﹣2x﹣8,则5x+2x=8+6 D、若 ,则2x+3(x﹣1)=63. 方程 的解是( )A、2 B、﹣3 C、 D、2或﹣34. 某商店的老板销售一种商品,他以不低于进价20%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价,若你想买下标价为360元的这种商品,且使商店老板愿出售,你最多可要求老板降价( )A、80元 B、100元 C、120元 D、160元5. 三角形的两边长分别是5和8,则第三边长不可能是( )A、3 B、5 C、7 D、96. 若 ,则下列不等式不一定成立的是( )A、 B、 C、 D、7. 不等式组 的解集在数轴上应表示为( )A、
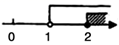 B、
B、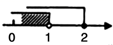 C、
C、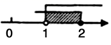 D、
D、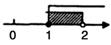 8. 若方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、9. 如果关于x , y的方程组 的解是二元一次方程3x﹣2y=2的一个解,那么m的值为( )A、14 B、﹣26 C、26 D、﹣1410. 若关于x的不等式 的解都能使不等式 成立,则a的取值范围是( )A、 或 B、 C、 D、11. 如图,在 中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G, , , ,则 的面积是( )
8. 若方程组 的解是 ,则方程组 的解是( )A、 B、 C、 D、9. 如果关于x , y的方程组 的解是二元一次方程3x﹣2y=2的一个解,那么m的值为( )A、14 B、﹣26 C、26 D、﹣1410. 若关于x的不等式 的解都能使不等式 成立,则a的取值范围是( )A、 或 B、 C、 D、11. 如图,在 中,点D,E,F分别在三边上,E是AC的中点,AD,BE,CF交于一点G, , , ,则 的面积是( )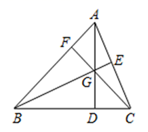 A、42 B、48 C、54 D、6012. 用正三角形和正六边形铺成一个平面,则在同一个顶点处,正三角形和正六边形的个数之比为( )A、4:1 B、1:1 C、1:4 D、4:1或1:113. 已知关于x , y的方程组 ,与 ,有相同的解,则a , b的值为( )A、 B、 C、 D、14. 已知 .当t=1时,s=13,当t=2时s=42,则当t=3时s=( )A、106.5 B、87 C、70.5 D、6915. 若关于
A、42 B、48 C、54 D、6012. 用正三角形和正六边形铺成一个平面,则在同一个顶点处,正三角形和正六边形的个数之比为( )A、4:1 B、1:1 C、1:4 D、4:1或1:113. 已知关于x , y的方程组 ,与 ,有相同的解,则a , b的值为( )A、 B、 C、 D、14. 已知 .当t=1时,s=13,当t=2时s=42,则当t=3时s=( )A、106.5 B、87 C、70.5 D、6915. 若关于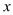 的不等式组 有且只有两个整数解,则
的不等式组 有且只有两个整数解,则  的取值范围是( ) A、 B、 C、 D、16. 如图,七边形 中, 的延长线交于点O,若 , 相邻的外角的和等于 ,则 的度数是( )
的取值范围是( ) A、 B、 C、 D、16. 如图,七边形 中, 的延长线交于点O,若 , 相邻的外角的和等于 ,则 的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
17. 不等式5x+8<3(2+x)的解集为 .18. 如果关于x的不等式2(x-1)<a+2与2x<4的解集相同,则a的值为 .19. 已知 则 .20. 足球比赛的计分规则为:胜一场积3分,平一场积1分,负1场积0分. 初三.(1)班在校足球联赛中踢了17场,其中负4场,共积31分,那么这支足球队胜了场.21. 若 、 、 满足 ,则 的值为 .22. 如图, +∠G= .
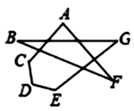 23. 如图,在 中, ,AD、BD、CD分别平分 的外角 ,内角 ,外角 ,以下结论:① ;② ;③ ;④ ,其中正确的结论有.
23. 如图,在 中, ,AD、BD、CD分别平分 的外角 ,内角 ,外角 ,以下结论:① ;② ;③ ;④ ,其中正确的结论有.
三、解答题
-
24. 解下列方程(组):(1)、3(2x-1)-(x-1)=2(8-2x)(2)、(3)、25. 解下列不等式(组):(1)、 ,并把它的解集在数轴上表示出来.
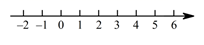 (2)、26. 已知关于x,y的方程组 ,甲由于看错了方程(1)中的a,得到方程组的解为 ,乙由于看错了方程(2)中的b,得到方程组的解 . 试求出方程组的符合题意解.27. 已知关于x、y的方程组 的解满足 .(1)、求a的取值范围;(2)、已知 ,且 ,求z的最大值.28. 如图,已知BD、CE是△ABC的两条高,直线BD、CE相交于点H .
(2)、26. 已知关于x,y的方程组 ,甲由于看错了方程(1)中的a,得到方程组的解为 ,乙由于看错了方程(2)中的b,得到方程组的解 . 试求出方程组的符合题意解.27. 已知关于x、y的方程组 的解满足 .(1)、求a的取值范围;(2)、已知 ,且 ,求z的最大值.28. 如图,已知BD、CE是△ABC的两条高,直线BD、CE相交于点H .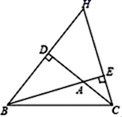 (1)、在图中找出与∠DBA相等的角,并说明理由;(2)、若∠BAC=110°,求∠DHE的度数.29. 如图,在五边形ABCDE中,∠C=90°,∠D=70°,∠E=130°,AP平分∠EAB , BP平分∠ABC , 求∠P的度数.
(1)、在图中找出与∠DBA相等的角,并说明理由;(2)、若∠BAC=110°,求∠DHE的度数.29. 如图,在五边形ABCDE中,∠C=90°,∠D=70°,∠E=130°,AP平分∠EAB , BP平分∠ABC , 求∠P的度数.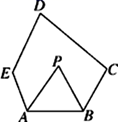 30. 某商场柜台销售每台进价分别为160元、120元的 、 两种型号的电器,下表是近两周的销售情况:
30. 某商场柜台销售每台进价分别为160元、120元的 、 两种型号的电器,下表是近两周的销售情况:销售时段
销售数量
销售收入
种型号
种型号
第一周
3台
4台
1200元
第二周
5台
6台
1900元
(进价、售价均保持不变,利润=销售收入—进货成本)
(1)、求A、B两种型号的电器的销售单价;(2)、若商场准备用不多于7500元的金额再采购这两种型号的电器共50台,求 种型号的电器最多能采购多少台?(3)、在(2)中商场用不多于7500元采购这两种型号的电器共50台的条件下,商场销售完这50台电器能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.31. Rt△ABC中,∠C=90°,点D、E分别是△ABC边AC、BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α .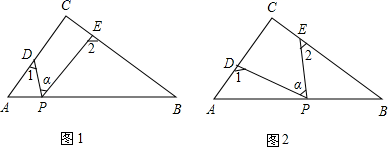
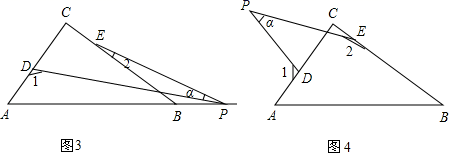 (1)、若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=;(2)、若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为;(3)、若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)、若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.
(1)、若点P在线段AB上,如图(1)所示,且∠α=60°,则∠1+∠2=;(2)、若点P在线段AB上运动,如图(2)所示,则∠α、∠1、∠2之间的关系为;(3)、若点P运动到边AB的延长线上,如图(3)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由;(4)、若点P运动到△ABC形外,如图(4)所示,则∠α、∠1、∠2之间有何关系?猜想并说明理由.