四川省成都市天府新区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-21 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、（a³）⁴＝a¹² B、a³•a²＝a⁶ C、3a•4a＝12a D、a⁶÷a²＝a³

查看试题解析
2. 下列四个手机APP图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2019年底，我国暴发了新型冠状病毒感染的肺炎疫情.已知新型冠状病毒的平均直径约为0.000000203米，该数据用科学记数法表示为（　　）

A、 2.03×10^﹣⁸ B、2.03×10^﹣⁷ C、2.03×10^﹣⁶ D、0.203×10^﹣⁶

查看试题解析
4. 下列事件中属于必然事件的是（）

A、任意买一张电影票，座位号是偶数 B、某射击运动员射击1次，命中靶心 C、掷一次骰子，向上的一面是6点 D、367人中至少有2人的生日相同

查看试题解析
5. 下列正确说法的个数是（）
①同位角相等；②等角的补角相等；③两直线平行，同旁内角相等；④在同一平面内，过一点有且只有一条直线与已知直线垂直.

A、1 B、2 C、3 D、4

查看试题解析
6. 能将一个三角形分成面积相等的两个三角形的一条线段是（）

A、三角形的高线 B、边的中垂线 C、三角形的中线 D、三角形的角平分线

查看试题解析
7. 已知 $(x - 2) (x + 3) = x^{2} + m x - 6$ ，则m的值是（）

A、-1 B、1 C、5 D、-5

查看试题解析
8. 一个等腰三角形的顶角是50°，则它的底角是（）

A、100° B、65° C、70° D、75°

查看试题解析
9. 如图在边长为a的正方形中挖掉一个边长为b的小正方形(a＞b)．把余下的部分剪拼成一个长方形，通过计算阴影部分的面积，验证了一个等式，则这个等式是（）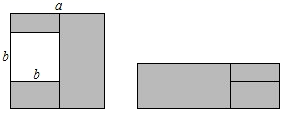

A、a²﹣2ab+b²＝(a﹣b)² B、a²﹣ab＝a(a﹣b) C、a²﹣b²＝(a﹣b)² D、a²﹣b²＝(a+b)(a﹣b)

查看试题解析
10. 如图，△ABC≌△ADE，点 D 落在 BC 上，且∠B＝55°，则∠EDC 的度数等于（）

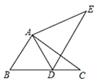A、50° B、60° C、80° D、70°

查看试题解析

二、填空题

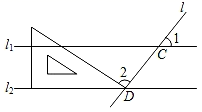
11. 已知∠1=30°，则∠1的补角的度数为度．

查看试题解析
12. 关于x的二次多项式x²+6x+m恰好是另一个多项式的平方，则常数项m＝．

查看试题解析
13. 如图，直线l₁//l₂ ，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝58°，则∠2的度数为．

查看试题解析
14. 如图，在 $R t △ A B C$ 中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=6，AB=17，则 $△ A B D$ 的面积是．

查看试题解析
15. 若x^m＝3，xⁿ＝5，则x^2m+n的值为．

查看试题解析
16. 一个不透明的布袋里装有3个球，其中2个红球，1个白球，它们除颜色外其余都相同．现再将n个白球放入布袋，搅匀后，使摸出1个红球的概率为 $\frac{2}{9}$ ，则n的值为．

查看试题解析
17. 如图，边长为5的正方形ABCD与直角三角板如图放置，延长CB与三角板的直角边相交于点E，则四边形AECF的面积为．

查看试题解析
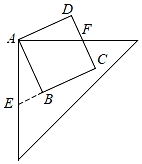18. 如图，正方形ABCD中，AE＝2cm，CG＝5cm．长方形EFGD的面积是11，四边形NGDH和MEDQ都是正方形，PQDH是长方形，则图中阴影部分的面积是cm² ．

查看试题解析
19. 如图， $△ A B C$ 中，CD⊥AB，垂足为D，CD＝BD＝5，AD＝4，点M从点B出发沿线段BA方向运动到点A停止，过点M作MN⊥AB，交折线BC﹣CA于点N，连接DN，AN，若 $△ A D N$ 与 $△ C N D$ 的面积相等，则线段BM的长为．

查看试题解析

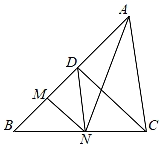
三、解答题

20.

(1)、计算：﹣3²﹣（2020﹣π）⁰﹣|﹣4|+（﹣ $\frac{1}{3}$ ）^﹣²；

(2)、计算：8m⁴•（﹣12m³n⁵）÷（﹣2mn）⁵ ．

查看试题解析
21. 先化简，再求值[（x+2y）²﹣（x+y）（x﹣y）﹣5y²]÷2x，其中 $x = - 2 ， y = \frac{1}{2}$ ．

查看试题解析
22. 如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A，B，C在小正方形的顶点上．

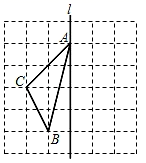
⑴在图中画出 $△ A B C$ 关于直线l成轴对称的 $△ A^{'} B^{'} C^{'}$ ；

⑵求 $△ A B C$ 的面积；

⑶在直线l上找一点P，使PB+PC的长最短，标出点P（保留作图痕迹）．

查看试题解析
23. 公路上，A，B两站相距25千米，C、D为两所学校，DA⊥AB于点A，CB⊥AB于点B，如图，已知DA＝15千米，现在要在公路AB上建一报亭H，使得C、D两所学校到H的距离相等，且∠DHC＝90°，问：H应建在距离A站多远处？学校C到公路的距离是多少千米？

查看试题解析

24. 在弹性限度内，某弹簧挂上物体后弹簧的长度与所挂物体的质量之间的关系如表：

所挂物体的质量/千克	0	1	2	3	4	5	6	7	8
弹簧的长度/cm	12	12.5	13	13.5	14	14.5	15	15.5	16

(1)、在这个变化过程中，自变量和因变量各是什么？

(2)、如果用x表示弹性限度内物体的质量，用y表示弹簧的长度，写出y与x的关系式．

(3)、如果该弹簧最大挂重量为25千克，当挂重为14千克时，该弹簧的长度是多少？

查看试题解析

25. 已知AB∥CD，点E为直线AB、CD所确定的平面内一点．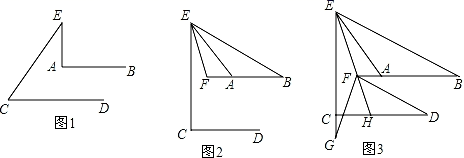

(1)、如图1，若AE⊥AB，求证：∠C+∠E=90°；

(2)、如图2，点F在BA的延长线上，连接BE、EF，若CE⊥CD，EF平分∠AEC，∠B=∠AEB，则∠BEF的度数为．

(3)、在（2）的条件下，如图3，过点F作∠BFG=∠BFE交EC的延长线于点G，连接DF，作∠DFG的平分线交CD于点H，当FD∥BE时，求∠CHF的度数．

查看试题解析
26. 若a，b，c为 $△ A B C$ 的三边．

(1)、化简：|a﹣b+c|+|c﹣a﹣b|﹣|a+b|；

(2)、若a，b，c都是正整数，且a²+b²﹣2a﹣8b+17＝0， $△ A B C$ 的周长．

查看试题解析
27. 某景区的三个景点A，B，C在同一线路上，甲、乙两名游客从景点A出发，步行到景点C；乙先乘景区观光车到景点B，在B处停留一段时间后，再步行到景点C，甲、乙两人同时到达最点C．甲、乙两人距景点A的路程y（米）与甲出发的时间x（分）之间的图象如图所示：

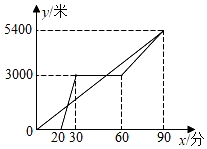(1)、甲步行的速度为米/分，乙步行时的速度为米/分；

(2)、分别写出甲游客从景点A出发步行到景点C和乙游客乘景区观光车时y与x之间的关系式；

(3)、问乙出发多长时间与甲在途中相遇？

查看试题解析
28. 如图1，在 $△ A B C$ 中，∠BAC＝90°，点D为AC边上一点，连接BD，点E为BD点连接CE，∠CED＝∠ABD，过点A作AG⊥CE，垂足为G，AG交ED于点F．

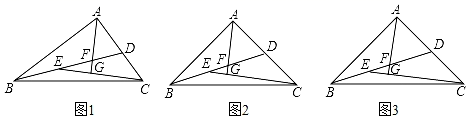(1)、判断AF与AD的数量关系，并说明理由；

(2)、如图2，若AC＝CE，点D为AC的中点，AB与AC相等吗？为什么？

(3)、在（2）的条件下，如图3，若DF＝5，求 $△ D E C$ 的面积．

查看试题解析