四川省成都市龙泉驿区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-21 类型:期末考试
一、单选题
-
1. 下列艺术字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式运算正确的是( )A、a2+a2=2a4 B、a2•a3=a5 C、(﹣3x)3÷(﹣3x)=﹣9x2 D、(﹣ab2)2=﹣a2b43. 下列事件中,属于必然事件的是( )A、抛出的篮球会下落 B、打开电视,正在播《新闻联播》 C、任意买一张电影票,座位号是3的倍数 D、校篮球队将夺得区冠军4. 计算(x+3)(x﹣3)的结果为( )A、x2+6x+9 B、x2﹣6x+9 C、x2+9 D、x2﹣95. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=30°,则∠1的度数为( )
2. 下列各式运算正确的是( )A、a2+a2=2a4 B、a2•a3=a5 C、(﹣3x)3÷(﹣3x)=﹣9x2 D、(﹣ab2)2=﹣a2b43. 下列事件中,属于必然事件的是( )A、抛出的篮球会下落 B、打开电视,正在播《新闻联播》 C、任意买一张电影票,座位号是3的倍数 D、校篮球队将夺得区冠军4. 计算(x+3)(x﹣3)的结果为( )A、x2+6x+9 B、x2﹣6x+9 C、x2+9 D、x2﹣95. 如图,一块直角三角尺的一个顶点落在直尺的一边上,若∠2=30°,则∠1的度数为( ) A、30° B、45° C、60° D、75°6. 下列各组数据,能构成三角形的是( )A、1cm , 2cm , 3cm B、2cm , 2cm , 5cm C、3cm , 4cm , 5cm D、7cm , 5cm , 1cm7. 如图,D , E是△ABC中BC边上的点,且BD=DE=EC , 那么( )
A、30° B、45° C、60° D、75°6. 下列各组数据,能构成三角形的是( )A、1cm , 2cm , 3cm B、2cm , 2cm , 5cm C、3cm , 4cm , 5cm D、7cm , 5cm , 1cm7. 如图,D , E是△ABC中BC边上的点,且BD=DE=EC , 那么( )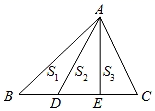 A、S1<S2<S3 B、S1>S2>S3 C、S1=S2=S3 D、S2<S1<S38. 李老师用直尺和圆规作已知角的平分线.
A、S1<S2<S3 B、S1>S2>S3 C、S1=S2=S3 D、S2<S1<S38. 李老师用直尺和圆规作已知角的平分线.作法:①以点O为圆心,适当长为半径画弧,交OA于点D,交OB于点E
②分别以点D、E为圆心,大于 DE的长为半径画弧,两弧在∠AOB的内部相交于点C.
③画射线OC,则OC就是∠AOB的平分线.
李老师用尺规作角平分线时,用到的三角形全等的判定方法是( )
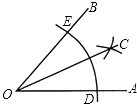 A、SSS B、SAS C、ASA D、AAS9. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()A、
A、SSS B、SAS C、ASA D、AAS9. 小明骑自行车上学,开始以正常速度匀速行驶,但行至中途时,自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合小明行驶情况的大致图象是()A、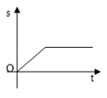 B、
B、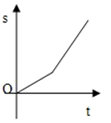 C、
C、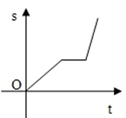 D、
D、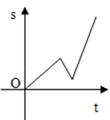 10. 如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )
10. 如图所示,在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,则∠A等于( )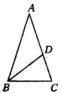 A、30° B、40° C、45° D、36°
A、30° B、40° C、45° D、36°二、填空题
-
11. 化简 (a+b)(a-b)= .12. 如图,用一段长为20米的篱笆围成一个一边靠墙(墙的长度不限)的长方形菜园ABCD , 设AB为x米,则菜园的面积y(平方米)与x(米)的关系式为 . (不要求写出自变量x的取值范围)
 13. 如图有一张直角三角形纸片,两直角边AC=4cm , BC=8cm , 把纸片的部分折叠,使点B与点A重合,折痕为DE , 则△ACD的周长为 .
13. 如图有一张直角三角形纸片,两直角边AC=4cm , BC=8cm , 把纸片的部分折叠,使点B与点A重合,折痕为DE , 则△ACD的周长为 .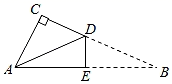 14. 一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为 .
14. 一只蚂蚁在如图所示的正方形地砖上爬行,蚂蚁停在阴影部分的概率为 .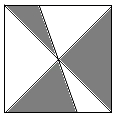 15. 若x2+2mx+9是完全平方式,则m= .16. 在△ABC中,BO平分∠ABC , CO平分∠ACB , 若∠O=120°,则∠A= .
15. 若x2+2mx+9是完全平方式,则m= .16. 在△ABC中,BO平分∠ABC , CO平分∠ACB , 若∠O=120°,则∠A= .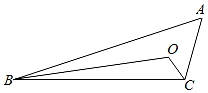 17. 如图,在Rt△ABC中,AC⊥BC , ∠A=30°,D为斜边AB的中点.若BC=2,则CD= .
17. 如图,在Rt△ABC中,AC⊥BC , ∠A=30°,D为斜边AB的中点.若BC=2,则CD= .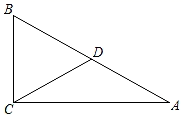 18. 若(x﹣3)(x2+ax+b)的积中不含x的二次项和一次项,则a+b的值为 .19. 如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b , 则∠AEG的度数度,再沿BF折叠成图c . 则图中的∠CFE的度数是度.
18. 若(x﹣3)(x2+ax+b)的积中不含x的二次项和一次项,则a+b的值为 .19. 如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b , 则∠AEG的度数度,再沿BF折叠成图c . 则图中的∠CFE的度数是度.
三、解答题
-
20.(1)、(﹣1)2020+(﹣ )2﹣(3.14﹣π)0;(2)、(a﹣1)(a+1)﹣(a﹣2)2;(3)、(20x2y﹣10xy2)÷(﹣5xy);(4)、(2x3y)2•(﹣2xy)+(﹣2x3y)3÷(2x2).21. 先化简,再求值:(x+3y)2﹣2x(x+2y)+(x﹣3y)(x+3y),其中x=﹣1,y=2.22. 如图所示,有两个村庄A , B在一公路CD的一侧,如果把A , B村庄的位置放在格点图中.
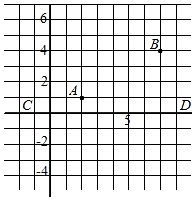
①请作出A点关于CD的对称点A′;
②若要在公路CD上修建一个菜鸟驿站P , 使得驿站到两个村庄的线段距离和最小,请作出P点的位置.
23. 如图,E、F分别在 、 上, , 与 互余, .求证: .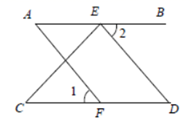 24. 已知:如图,点E , D , B , F在同一条直线上,AD∥CB , ∠E=∠F , DE=BF . 求证:AE=CF . (每一行都要写依据)
24. 已知:如图,点E , D , B , F在同一条直线上,AD∥CB , ∠E=∠F , DE=BF . 求证:AE=CF . (每一行都要写依据)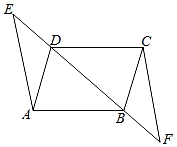 25. 已知:AB=AC , AF=AG , AE⊥BG交BG的延长线于E , AD⊥CF交CF的延长线于D . 求证:AD=AE .
25. 已知:AB=AC , AF=AG , AE⊥BG交BG的延长线于E , AD⊥CF交CF的延长线于D . 求证:AD=AE .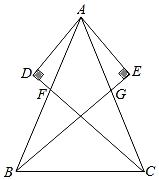 26. 如图,C为线段AE上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交与点P,BE与CD交于点Q,连接PQ.
26. 如图,C为线段AE上一动点,(不与点A、E重合),在AE同侧分别作正△ABC和正△CDE,AD与BE交于点O,AD与BC交与点P,BE与CD交于点Q,连接PQ.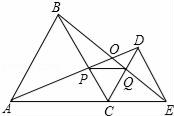
求证:
(1)、AD=BE(2)、△APC≌△BQC(3)、△PCQ是等边三角形.27. 如图1,∠FBD=90°,EB=EF , CB=CD .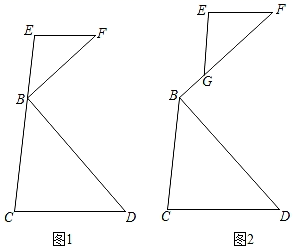 (1)、求证:EF∥CD;(2)、如图2所示,若将△EBF沿射线BF平移,即EG∥BC , ∠FBD=90°,EG=EF , CB=CD , 请问(1)中的结论是否仍成立?请证明.28.
(1)、求证:EF∥CD;(2)、如图2所示,若将△EBF沿射线BF平移,即EG∥BC , ∠FBD=90°,EG=EF , CB=CD , 请问(1)中的结论是否仍成立?请证明.28.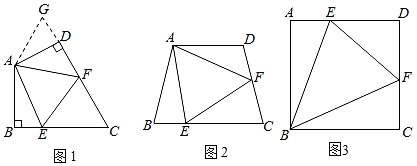 (1)、如图1,在四边形ABCD中,AB=AD , ∠BAD=100°,∠B=∠ADC=90°.E , F分别是BC , CD上的点.且∠EAF=50°.探究图中线段EF , BE , FD之间的数量关系.
(1)、如图1,在四边形ABCD中,AB=AD , ∠BAD=100°,∠B=∠ADC=90°.E , F分别是BC , CD上的点.且∠EAF=50°.探究图中线段EF , BE , FD之间的数量关系.小明同学探究的方法是:延长FD到点G , 使DG=BE , 连接AG , 先证明△ABE≌△ADG , 再证明△AEF≌△AGF , 可得出结论,他的结论是(直接写结论,不需证明);
(2)、如图2,若在四边形ABCD中,AB=AD , ∠B+∠D=180°,E , F分别是BC , CD上的点,且2∠EAF=∠BAD , 上述结论是否仍然成立,若成立,请证明,若不成立,请说明理由;(3)、如图3,四边形ABCD是边长为7的正方形,∠EBF=45°,直接写出△DEF的周长.