四川省成都市成华区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-21 类型：期末考试

进入出卷网下载

一、单选题

1. 如图，在线段 $P A$ 、 $P B$ 、 $P C$ 、 $P D$ 中，长度最小的是（）

A、线段 $P A$ B、线段 $P B$ C、线段 $P C$ D、线段 $P D$

查看试题解析
2. 中国的方块字中有些具有对称性．下列美术字是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 某种新型冠状病毒的直径为0.000000053米，将0.000000053用科学记数法表示为（）

A、53×10^﹣⁸ B、5.3×10^﹣⁷ C、5.3×10^﹣⁸ D、5.3×10^﹣⁹

查看试题解析
4. “对顶角相等”，这一事件是（）

A、必然事件 B、不确定事件 C、随机事件 D、不可能事件

查看试题解析
5. 下列长度的三条线段，能组成三角形的是（）

A、4，5，9 B、6，7，14 C、4，6，10 D、8，8，15

查看试题解析
6. 下列运算正确的是（）

A、（a³）²＝a⁶ B、a²•a³＝a⁶ C、（a+b）²＝a²+b² D、a²+a³＝a⁵

查看试题解析
7. 如图，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（）

A、∠A=∠D B、AB=DC C、∠ACB=∠DBC D、AC=BD

查看试题解析
8. 如图，直线AD∥BC，若∠1＝74°，∠BAC＝56°，则∠2的度数为（）

A、70° B、60° C、50° D、40°

查看试题解析
9. 如图，在△ABC 中，AB=AC，∠C=70°，△AB′C′与△ABC 关于直线 EF对称，∠CAF=10°，连接 BB′，则∠ABB′的度数是（）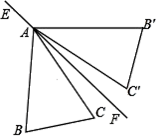

A、30° B、35° C、40° D、45°

查看试题解析
10. 第一次“龟兔赛跑”，兔子因为在途中睡觉而输掉比赛，很不服气，决定与乌龟再比一次，并且骄傲地说，这次我一定不睡觉，让乌龟先跑一段距离我再去追都可以赢.结果兔子又一次输掉了比赛，则下列函数图象可以体现这次比赛过程的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 已知∠1=30°，则∠1的补角的度数为度．

查看试题解析
12. 某十字路口的交通信号灯每分钟红灯亮30秒，绿灯亮25秒，黄灯亮5秒，当你抬头看信号灯时，是绿灯的概率为．

查看试题解析
13. 若a²+b²=6，a+b=3，则ab的值为．

查看试题解析
14. 如图，在 $Δ A B C$ 中，分别以点A和点C为圆心，大于 $\frac{1}{2} A C$ 长为半径画弧，两弧相交于点M、N；作直线MN分别交BC、AC于点D、点E ，若 $A E = 3 m$ ， $Δ A B D$ 的周长为13cm ，则 $Δ A B C$ 的周长为.

查看试题解析
15. 若2^x=5，2^y=3，则2^2x⁺^y= ．

查看试题解析
16. 如图，已知1₁∥l₂ ， ∠C＝90°，∠1＝40°，则∠2的度数是．

查看试题解析
17. 如图，在4×4正方形网格中，黑色部分的图形构成一个轴对称图形，现在任选取一个白色的小正方形并涂黑，使图中黑色部分的图形仍然构成一个轴对称图形的概率是．

查看试题解析
18. 如图，图1是“杨辉三角”数阵；图2是（a+b）ⁿ的展开式（按b的升幂排列）．若（1+x）⁴⁵的展开式按x的升幂排列得：（1+x）⁴⁵＝a₀+a₁x+a₂x²+…+a₄₅x⁴⁵ ，则a₂＝．

查看试题解析
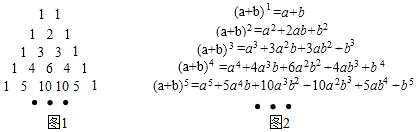19. 如图，AD，BE在AB的同侧，AD＝2，BE＝2，AB＝4，点C为AB的中点，若∠DCE＝120°，则DE的最大值是．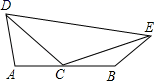

查看试题解析

三、解答题

20. 计算：

(1)、（﹣1）²⁰²⁰﹣（2020﹣π）⁰+（﹣ $\frac{1}{3}$ ）^﹣²﹣|﹣2|；

(2)、[（2x²）³﹣6x³（x³﹣2x²）]÷2x⁴ ．

查看试题解析
21.

(1)、先化简，再求值：（x+1）（x﹣1）+（2x﹣1）²﹣2x（2x﹣1），其中x＝﹣2．

(2)、先化简，再求值：[（2x﹣y）²+（2x﹣y）（2x+y）]÷4x，其中x＝2，y＝﹣1．

查看试题解析

22. 为了增强学生的安全意识，某校组织了一次全校2500名学生都参加的“安全知识”考试．阅卷后，学校团委随机抽取了100份考卷进行分析统计，发现考试成绩（

x

分）的最低分为51分，最高分为满分100分，并绘制了如下尚不完整的统计图表．请根据图表提供的信息，解答下列问题：

分数段（分）	频数（人）	频率
$51 \leq x < 61$	$a$	0.1
$61 \leq x < 71$	18	0.18
$71 \leq x < 81$	$b$	$n$
$81 \leq x < 91$	35	0.35
$91 \leq x < 101$	12	0.12
合计	100	1

(1)、填空：

a =

，

b =

，

n =

；

(2)、将频数分布直方图补充完整；

(3)、该校对考试成绩为

91 \leq x \leq 100

的学生进行奖励，按成绩从高分到低分设一、二、三等奖，并且一、二、三等奖的人数比例为1：3：6，请你估算全校获得二等奖的学生人数.

查看试题解析

23. 如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，BD=CE，BE、CD相交于点0；

求证：

(1)、 $Δ D B C ≅ Δ E C B$

(2)、 $O B = O C$

查看试题解析
24. 某种型号汽车油箱容量为63升，每行驶100千米耗油8升．设一辆加满油的该型号汽车行驶路程为x千米．

(1)、写出汽车耗油量y（升）与x之间的关系式；

(2)、写出油箱内剩余油量Q（升）与x之间的关系式；

(3)、为了有效延长汽车使用寿命，厂家建议汽车油箱内剩余油量为油箱容量的 $\frac{1}{7}$ 时必须加油．按此建议，问该辆汽车最多行驶多少千米必须加油？

查看试题解析
25. 已知：如图，点B在线段AD上， $△$ ABC和 $△$ BDE都是等边三角形，且在AD同侧，连接AE交BC于点G，连接CD交BE于点H，连接GH．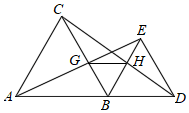

(1)、求证：AE=CD；

(2)、求证：AG=CH；

(3)、求证：GH∥AD．

查看试题解析
26. 图1和图2的大正方形都是由一些长方形和小正方形组成的．观察图形，完成下列各题：

(1)、如图1，求S_大正方形的方法有两种：S_大正方形=(x+y)² ，同时，S_大正方形=S_①+S_②+S_③+S_④= ．所以图1可以用来解释等式：；同理图2可以用来解释等式：．

(2)、已知a+b+c=6，ab+bc+ca=11，利用上面得到的等式，求a²+b²+c²的值．

查看试题解析
27. 王老师和小颖住同一小区，小区距离学校2400米．王老师步行去学校，出发10分钟后小颖才骑共享单车出发．小颖途经学校继续骑行若干米到达还车点后，立即跑步返回学校．小颖跑步比王老师步行每分钟快70米．设王老师步行的时间为x（分钟），图1中线段OA和折线B﹣C﹣D分别表示王老师和小颖离开小区的路程y（米）与x（分钟）的关系：图2表示王老师和小颖两人之间的距离S（米）与x（分钟）的关系（不完整）．

(1)、求王老师步行的速度和小颍出发时王老师离开小区的路程；

(2)、求小颖骑共享单车的速度和小颖到达还车点时王老师、小颖两人之间的距离；

(3)、在图2中，画出当25≤x≤30时S关于x的大致图象（要求标注关键数据）．

查看试题解析
28.

(1)、如图1，在 $△$ ABC中，AB=4，AC=6，AD是BC边上的中线，延长AD到点E使DE=AD，连接CE，把AB，AC，2AD集中在 $△$ ACE中，利用三角形三边关系可得AD的取值范围是；

(2)、如图2，在 $△$ ABC中，AD是BC边上的中线，点E，F分别在AB，AC上，且DE⊥DF，求证：BE+CF＞EF；

(3)、如图3，在四边形ABCD中，∠A为钝角，∠C为锐角，∠B+∠ADC=180°，DA=DC，点E，F分别在BC，AB上，且∠EDF= $\frac{1}{2}$ ∠ADC，连接EF，试探索线段AF，EF，CE之间的数量关系，并加以证明．

查看试题解析