湖南省郴州市2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-21 类型：期末考试

进入出卷网下载

一、单选题

1. 若 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ 是方程 $3 x + a y = 1$ 的一个解，则a的值是（）

A、 $1$ B、 $- 1$ C、 $2$ D、 $- 2$

查看试题解析
2. 下列各式计算正确的是（）

A、 ${(a^{2})}^{3} = a^{5}$ B、 $a^{4} \cdot a^{2} = a^{2}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(a b)}^{3} = a^{3} b^{3}$

查看试题解析
3. 二元一次方程组 ${\begin{matrix} x + y = 2 \\ x - y = - 2 \end{matrix}$ 的解是（）

A、 ${\begin{matrix} x = 0 \\ y = 2 \end{matrix}$ B、 ${\begin{matrix} x = 2 \\ y = 0 \end{matrix}$ C、 ${\begin{matrix} x = 1 \\ y = 4 \end{matrix}$ D、 ${\begin{matrix} x = 1 \\ y = 1 \end{matrix}$

查看试题解析
4. 下图是我国几家银行的标志，其中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 如果 $3^{5} \times 9 = 3^{n}$ ，则n的值为（）

A、6 B、7 C、8 D、9

查看试题解析
6. 如图，直线a，b被直线c所截，下列条件中，不能判定a∥b（）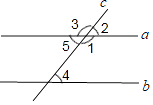

A、∠2=∠4 B、∠1+∠4=180° C、∠5=∠4 D、∠1=∠3

查看试题解析
7. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是8.4环，方差分别是 $s^{2}_{甲} =0 .5$ ， $s^{2}_{乙} =0 .7$ ， $s^{2}_{丙} =0 .9$ ， $s^{2}_{丁} =1 .5$ ．在这次射击测试中，成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
8. 如果二次三项式 $x^{2} + a x + 2$ 可分解为 $(x - 1) (x + b)$ ，则 $a + b$ 的值为（）

A、 $- 2$ B、 $- 5$ C、3 D、5

查看试题解析
9. 在同一平面内，设a、b、c是三条互相平行的直线，已知a与b的距离为4cm，b与c的距离为1cm，则a与c的距离为（）

A、1cm B、3cm C、5cm或3cm D、1cm或3cm

查看试题解析

二、填空题

10. 计算： $2 a \cdot a^{2} - a^{3} =$ ．

查看试题解析
11. 因式分解： ${xy}^{2} + 2 xy + x =$ ．

查看试题解析
12. 已知方程 $2 x + y - 1 = 0$ ，用含x的代数式表示y的形式为.

查看试题解析
13. 一组数据：2，2，1，4，4，4的中位数是.

查看试题解析
14. 若 $x - 3 y = 2$ 且 $3 x - y = 6$ ，则 $y - x$ 的值为.

查看试题解析
15. 如图，三角形ABC绕点A逆时针旋转90°到三角形 $A B^{'} C^{'}$ 的位置.已知 $∠ B A C = 35^{°}$ ，则 $∠ B^{'} A C =$ 度.

查看试题解析
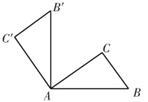16. 如图，直线 $a ∥ b$ ，三角板的直角顶点A落在直线a上，两条边分别交直线b于B ， C两点.若 $∠ 1 = 25^{°}$ ，则 $∠ 2 =$ 度.

查看试题解析
17. 如图， $A D ∥ B C$ ， $A D = B C = 4$ ，且三角形ABC的面积为6，则点C到AD的距离是.

查看试题解析
18. 将长方形ABCD纸片按如图所示方式折叠，使得 $∠ A^{'} E B^{'} = 50^{°}$ ，其中EF ， EG为折痕，则 $∠ A E F +$ $∠ B E G =$ 度.

查看试题解析

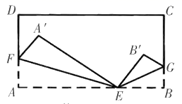
三、解答题

19. 解方程组： ${\begin{array}{l} 2 x - 3 y = 7, ① \\ x + 3 y = - 1. ② \end{array}$

查看试题解析
20. 先化简，再求值：
(x＋2)(x－2)＋x(4－x)，其中x＝ $\frac{1}{4}$ .

查看试题解析
21. 如图，三角形ABC和直线MN ，且三角形ABC的顶点在网格的交点上.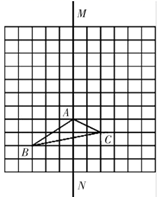

①画出三角形ABC向上平移4小格后的三角形 $A_{1} B_{1} C_{1}$ ；

②画出三角形ABC关于直线MN对称的三角形 $A_{2} B_{2} C_{2}$

（以上作图不要求写作法）

查看试题解析
22. 推理填空：
如图， $D E ∥ B C$ ， $∠ A D E = ∠ E F C$ ，将说明 $∠ 1 = ∠ 2$ 成立的理由填写完整.

解：因为 $D E ∥ B C$ （已知），

所以 $∠ A D E = ∠ A B C$ （）

又因为 $∠ A D E = ∠ E F C$ （已知），

所以 $∠ A B C = ∠ E F C$ （等量代换），

所以（同位角相等，两直线平行），

所以 $∠ 1 = ∠ 2$ （）

查看试题解析
23. 小欣打算购买气球装扮好朋友小岩的生日派对现场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同.由于布置的需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为多少元?

查看试题解析

24. 为准备参加某市2019年度中小学生机器人竞赛，学校对甲、乙两支机器人制作小队所创作的机器人分别从创意、设计、编程与制作三方面进行量化，各项量化满分100分，根据量化结果择优推荐.它们三项量化得分如下表：

量化项目	量化得分
量化项目	甲队	乙队
创意	85	72
设计	70	66
编程与制作	64	84

(1)、如果根据三项量化的平均分择优推荐，哪队将被推荐参赛？

(2)、根据本次中小学生机器人竞赛的主题要求，如果学校根据创意、设计、编程与制作三项量化得分按

5 ： 3 ： 2

的比例确定每队最后得分的平均分择优推荐，哪队将被推荐参赛？并对另外一队提出合理化的建议.

查看试题解析

25. 如图，BF ， DE分别是 $∠ A B D$ ， $∠ B D C$ 的平分线，且 $B F ⊥ D E$ ，垂足为点E ， BF交DC于点F.

(1)、试说明 $A B ∥ C D$ ；

(2)、若 $∠ D B F = 55^{°}$ ，试求 $∠ E F D$ 的度数.

查看试题解析
26. 阅读某同学对多项式 $(x^{2} - 4 x + 2) (x^{2} - 4 x + 6) + 4$ 进行因式分解的过程，并解决问题：
解：设 $x^{2} - 4 x = y$ ，

原式 $= (y + 2) (y + 6) + 4$ （第一步）

$= y^{2} + 8 y + 16$ （第二步）

$= {(y + 4)}^{2}$ （第三步）

$= {(x^{2} - 4 x + 4)}^{2}$ （第四步）

(1)、该同学第二步到第三步的变形运用了________（填序号）；

A、提公因式法 B、平方差公式 C、两数和的平方公式 D、两数差的平方公式

(2)、该同学在第三步用所设的的代数式进行了代换，得到第四步的结果，这个结果能否进一步因式分解？（填“能”或“不能”）.如果能，直接写出最后结果.

(3)、请你模仿以上方法尝试对多项式 $(x^{2} + 6 x) (x^{2} + 6 x + 18) + 81$ 进行因式分行解.

查看试题解析
27. 如图，点O为直线AB上一点，过点O作射线OC ，使 $∠ B O C = 135^{°}$ .将一个含45°角的直角三角板OMN的一个顶点放在点O处，斜边OM与直线AB重合，另外两条直角边ON ， MN都在直线AB的下方.

(1)、将图1中的三角板OMN绕着点O逆时针旋转90°，如图2所示，请问OM是否平分 $∠ C O N$ ？请说明理由；

(2)、将图2中的三角板OMN绕点O逆时针继续旋转到图3的位置所示，使得ON在 $∠ A O C$ 的内部，请探究 $∠ A O M$ 与 $∠ C O N$ 之间的数量关系，并说明理由；

(3)、将图1中的三角板OMN绕点O按每秒 ${2.5}^{°}$ 的速度沿逆时针方向旋转一周，在旋转的过程中，第t秒时，直角边ON所在直线恰好平分锐角 $∠ A O C$ ，则t的值为（直接写出结果）.

查看试题解析