湖南长沙湘一芙蓉、一中双语2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2020-09-21 类型：期末考试

进入出卷网下载

一、单选题

1. 下列实数.是无理数的是（）

A、 $\sqrt{9}$ B、 $\sqrt{- 8}$ C、3 .14 D、 $\sqrt{5}$

查看试题解析
2. 将方程3x﹣y＝1变形为用x的代数式表示y（　　）

A、3x＝y+1 B、x＝ $\frac{1 + y}{3}$ C、y＝1﹣3x D、y＝3x﹣1

查看试题解析
3. 若 $x > y$ ，则下列判断中错误的是（）

A、 $x + 2 > y + 2$ B、 $x - 1 > y - 1$ C、 $5 x > 5 y$ D、 $- 3 x > - 3 y$

查看试题解析
4. 下列四个图形.∠1与∠2是内错角的是（）

A、 B、 C、 D、

查看试题解析
5. 以下调查.适宜抽样调查的是（）

A、调查本班同学的体重 B、湖南卫视跨年演唱会的收视率 C、长沙地铁 5 号线对乘客的安检 D、全国人口普查

查看试题解析
6. 已知 ${\begin{array}{l} x = a \\ y = b \end{array}$ 是方程组 ${\begin{array}{l} 2 x + y = 3 \\ 3 x - 2 y = 7 \end{array}$ 的解，则 $5 a - b$ 的值是（）

A、10 B、-10 C、14 D、21

查看试题解析
7. 在平面直角坐标系.将点P（﹣2，1）向右平移3个单位长度，再向上平移4个单位长度得到点P′的坐标是（）

A、（2，4） B、（1，5） C、（1，-3） D、（-5，5）

查看试题解析
8. 如图，下列条件.能判断AB∥CD的是（）

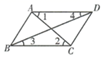A、∠BAD=∠BCD B、∠BAC=∠ACD C、∠1=∠2 D、∠3=∠4

查看试题解析
9. 一个关于x的一元一次不等式组的解集在数轴上的表示如图，则该不等式组的解集是（）

A、x＞1 B、x≥1 C、x＞3 D、x≥3

查看试题解析
10. 下列命题.假命题是（　　）

A、如果两条直线都与第三条直线平行，那么这两条直线也互相平行 B、在同一平面内，过一点有且只有一条直线与已知直线垂直 C、两条直线被第三条直线所截，同旁内角互补 D、两直线平行，内错角相等

查看试题解析
11. 若不等式组 ${\begin{array}{l} x \geq a \\ x \leq b \end{array}$ 无解，则不等式组 ${\begin{array}{l} x > 3 - a \\ x < 3 - b \end{array}$ 的解集是（）

A、 $x > 3 - a$ B、 $x < 3 - b$ C、 $3 - a < x < 3 - b$ D、无解

查看试题解析
12. 如图，在平面直角坐标系.点 A₁、A₂、A₃、A₄、A₅、A₆ 的坐标依次为 A₁(0，1)， A₂(1，1)，A₃(1，0)，A₄(2，0)，A₅(2，1)，A₆(3，1)，…按此规律排列，则点 A₂₀₂₀的坐标是（）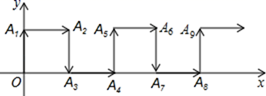

A、(1009，1) B、(1009，0) C、(1010，1) D、(1010，0)

查看试题解析

二、填空题

13. 已知点A(a-2，a)在y轴上，则A点坐标为．

查看试题解析
14. 在一个扇形统计图.有一个扇形占所在圆的40%，则这个扇形圆心角是．

查看试题解析
15. 把命题“对顶角相等”改写成“如果…那么…”的形式是.

查看试题解析
16. 某年级有学生246人，其中男生比女生人数的2倍少3人，问男女学生各多少人，设女生人数为x人，男生人数为y人，可列方程组为．

查看试题解析
17. 若关于x的不等式组 ${\begin{cases} x + 6 < 2 + 3 x \\ \frac{a + 2 x}{4} > x \end{cases}$ 有且只有四个整数解，则实数a的取值范围是．

查看试题解析
18. 对非负实数x“四舍五入”到个位的值记为（x），即当 n 为非负整数时，若 $n - \frac{1}{2} \leq x$ ＜ $n + \frac{1}{2}$ ，则（x）=n，如（0.46）=0，（3.67）=4．则下列结论正确的有(填所有正确的序号)．
①（1.493）=1

②（2x）=2(x)

③若 $\frac{1}{2} x - 1 = 4$ ，则实数x的取值范围是9≤?<11

④当 x≥ 0，m 为非负整数时，有（m+2013x）=m+(2013x)

⑤（x+y）=(x)+(y)

查看试题解析

三、解答题

19. 计算：

(1)、 $(- 2) \times \sqrt{{(- 4)}^{2}} - \sqrt{9}$

(2)、 $\sqrt[3]{- 27} - \sqrt{0} - \sqrt{\frac{1}{4}} + \sqrt[3]{1 - \frac{63}{64}}$

查看试题解析
20.

(1)、解方程组： ${\begin{array}{l} 3 x - y = 2 ① \\ 9 x + 8 y = 17 ② \end{array}$ ．

(2)、解不等式组 ${\begin{array}{l} \frac{x - 3}{2} + 3 \geq x + 1 ① \\ 1 - 3 (x - 1) < 8 - x ② \end{array}$ 并把解集在数轴上表示出来．

查看试题解析
21. 某市举行“建国70周年”征文比赛，已知每篇参赛征文成绩记m分(60≤m≤100)，组委会从1000篇征文随机抽取了部分参赛征文，统计了它们的成绩，并绘制了如下不完整的两幅统计图表．

请根指以上信息，解答下列问题

(1)、征文比赛成绩频数分布表.a= ， b= ， c= ．

(2)、补全征文比赛成绩频数分布直方图；

(3)、若80分以上(含80分)的征文将被评为一等奖，试估计全市获得一等奖征文的篇数．

查看试题解析
22. 如图，在平面直角坐标系.已知A(0，a)，B(b，0)，C(b，c)三点，其中 a，b，c 满足关系式|a－2|＋(b－3)²＝0，(c－4)²≤0．

(1)、求 a，b，c 的值；

(2)、如果在第二象限内有一点P(m， $\frac{1}{2}$ )，请用含m 的式子表示四边形ABOP 的面积；

查看试题解析
23. 如图，已知BD⊥AC，EF⊥AC，D，F分别为垂足，G是AB上一点，且∠1＝∠2.试说明：∠AGD＝∠ABC．

查看试题解析
24. 一中双语举行书画大赛，准备购买甲、乙两种文具，奖励在活动中表现优秀的师生，已知购买2个甲种文具，1个乙种文具共需要花费35元，购买1个甲种文具，3个乙种文具共需要花费30元．

(1)、求购买一个甲种文具，一个乙种文具各需多少钱？

(2)、若学校计划购买这两种文具共120个，投入资金不少于955元，又不多于1000元，问有多少种购买方案？

查看试题解析
25. 如果一元一次方程的根是一元一次不等式组的解，则称该一元一次方程为该不等式组的关联方程．

(1)、在方程①x-（3x+1）＝﹣5；② $\frac{2 x}{3} + 1 = 0$ ；③3x﹣1＝0.不等式组 ${\begin{array}{l} - x + 2 > x - 5 \\ 3 x - 1 > - x + 2 \end{array}$ 的关联方程是（填序号）；

(2)、若不等式组 ${\begin{array}{l} x - 2 < 1 \\ 1 + x > - x + 2 \end{array}$ 的某个关联方程的根是整数，则这个关联方程可以是（写出一个即可）；

(3)、若方程 $\frac{1}{2} - \frac{1}{2} x = \frac{1}{2} x ， 3 + x = 2 (x + \frac{1}{2})$ 都是关于x的不等式组 ${\begin{array}{l} x - 2 ⩽ m \\ x < 2 x - m \end{array}$ 的关联方程，直接写出m的取值范围．

查看试题解析
26. 如图所示，在平面直角坐标系.点 $C (m ， m)$ 在一三象限角平分线上，点 $B (n ， 0)$ 在x轴上，且m= $\sqrt{n - 2}$ + $\sqrt{2 - n}$ +4，点A在y轴的正半轴上；四边形 $A O B C$ 的面积为6

(1)、求点A的坐标；

(2)、P为 $A B$ 延长线上一点， $P Q // O C$ ，交 $C B$ 延长线于Q ，探究 $∠ O A P$ 、 $∠ A B Q$ 、 $∠ Q$ 的数量关系并说明理由；

(3)、作 $A D$ 平行 $C B$ 交 $CO$ 延长线于D ， $B E$ 平分 $∠ C B x$ ， $B E$ 反向延长线交 $CO$ 延长线于，若设 $∠ A D O = α$ ， $∠ F = β$ ，试求 $α + 2 β$ 的值．

查看试题解析