四川省南充市营山县2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-21 类型:期末考试
一、单选题
-
1. 下面的四个图形中,∠1与∠2是对顶角的是( )A、
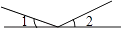 B、
B、 C、
C、 D、
D、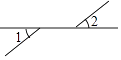 2. 下列实数中最大的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点M(a,b)位于第一象限,则点N(-a,-b)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 二元一次方程3x + 2y = 12的解可以是( )A、 B、 C、 D、5. 如果 ,那么下列结论错误的是( )A、 ; B、 ; C、 ; D、 .6. 下列调查中,适合抽样调查的是( )A、了解某班同学的身高情况 B、了解神舟飞船的设备零件的质量情况 C、了解某班同学到学校乘坐的交通工具情况 D、了解全市学生在疫情期间的线上学习情况7. 不等式4(x-1)<3x-2的正整数解的个数是( )A、0 B、1 C、2 D、38. 要直观介绍空气中各成分的百分比,最适合使用的统计图是( )A、条形图 B、扇形图 C、折线图 D、直方图9. 在“幻方拓展课程”探索中,小明在如图的3×3方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则x﹣y=( )
2. 下列实数中最大的是( )A、 B、 C、 D、3. 在平面直角坐标系中,点M(a,b)位于第一象限,则点N(-a,-b)位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 二元一次方程3x + 2y = 12的解可以是( )A、 B、 C、 D、5. 如果 ,那么下列结论错误的是( )A、 ; B、 ; C、 ; D、 .6. 下列调查中,适合抽样调查的是( )A、了解某班同学的身高情况 B、了解神舟飞船的设备零件的质量情况 C、了解某班同学到学校乘坐的交通工具情况 D、了解全市学生在疫情期间的线上学习情况7. 不等式4(x-1)<3x-2的正整数解的个数是( )A、0 B、1 C、2 D、38. 要直观介绍空气中各成分的百分比,最适合使用的统计图是( )A、条形图 B、扇形图 C、折线图 D、直方图9. 在“幻方拓展课程”探索中,小明在如图的3×3方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则x﹣y=( )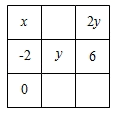 A、2 B、4 C、6 D、810. 在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为( )A、20° B、55° C、20°或 125° D、20°或55°
A、2 B、4 C、6 D、810. 在同-平面内,若∠A与∠B的两边分别垂直,且∠A比∠B的3倍少40°,则∠A的度数为( )A、20° B、55° C、20°或 125° D、20°或55°二、填空题
-
11. 4的算术平方根是 , 9的平方根是 , ﹣27的立方根是 .12. 9月3日是抗日战争胜利纪念日,某校为了解学生对抗日战争的知晓情况,从全校3000名学生中,随机抽取了100名学生进行调查,这次调查的样本容量是13. 点P(m﹣1,m+3)在平面直角坐标系的x轴上,则P点坐标是 .14. 若 ,则 的值为 .15. 在直线AB上有一点O,OC OD,∠AOC=30°,则∠BOD的度数是 .16. 已知关于x的不等式组 有且只有四个整数解,则a的取值范围为
三、解答题
-
17. 计算:18. 解方程组: .19. 解不等式组 ,把解集在数轴上表示出来.并求出其中的负整数解.20. 已知 `是 经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:(1)、观察表中各对应点坐标的变化,求出a、b、c的值:(2)、在平面直角坐标系中画出 ,求出 的面积.21. 完成下面的证明:
已知:如图, , 与 交于E点.求证: .
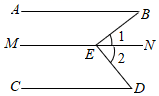
证明:过E作
(已知)
().
()
又
().
().
又 (已知),
(等量代换)
22. 随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗IL的情况下,所行驶的路程(单位:km)进行统计分析,结果如图所示:(注:记A为12<A<12.5,B为12.5SB<13,C为13SC<13.5,D为13.5≤D<14,E为14SE<14.5)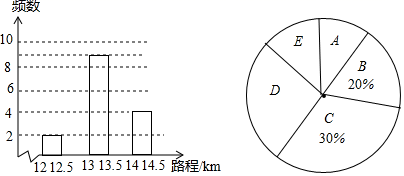
请依据统计结果回答以下问题:
(1)、试求进行该试验的车辆数:(2)、请补全频数分布直方图:(3)、若该市有这种型号的汽车约900辆(不考虑其他因素),请利用上述统计数据初步预测,该市约有多少辆该型号的汽车,在耗油IL的情况下可以行驶13km(含13km)以上?23. A地至B地的航线长9750km,-架飞机从A地顺风飞往B地需12.5h,它逆风飞行同样的航线需13h,求飞机无风时的平均速度与风速.24. 为积极响应政府提出的“绿色发展•低碳出行”号召,某社区决定购置一批共享单车.经市场调查得知,购买3辆男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.(1)、求男式单车和女式单车的单价;(2)、该社区要求男式单车比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?25. 如图1,已知PQ//MN,且∠BAM=2∠BAN.
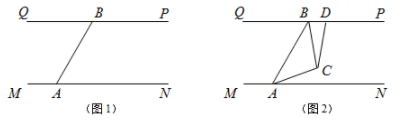 (1)、求∠BAN的度数;(2)、如图1所示,射线AM绕点A开始顺时针旋转至AN便立即回转至AM位置,射线BP绕点B开始顺时针旋转至BQ便立即回转至BP位置.若AM转动的速度是每秒2度,BP转动的速度是每秒1度,若射线BP先转动30秒,射线AM才开始转动,在射线BP到达BQ之前,射线AM转动多少秒?两射线互相平行.(3)、如图2,若两射线分别绕点A,B顺时针方向同时转动,速度同(2),在射线AM到达AN之前,若两射线交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系:若改变,请说明理由.
(1)、求∠BAN的度数;(2)、如图1所示,射线AM绕点A开始顺时针旋转至AN便立即回转至AM位置,射线BP绕点B开始顺时针旋转至BQ便立即回转至BP位置.若AM转动的速度是每秒2度,BP转动的速度是每秒1度,若射线BP先转动30秒,射线AM才开始转动,在射线BP到达BQ之前,射线AM转动多少秒?两射线互相平行.(3)、如图2,若两射线分别绕点A,B顺时针方向同时转动,速度同(2),在射线AM到达AN之前,若两射线交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系:若改变,请说明理由.