湖南省常德市市区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-21 类型:期末考试
一、单选题
-
1. 下列四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列计算正确的是( )A、 B、 C、 D、3. 市直某中学足球队的18名队员的年龄情况如下表:
2. 下列计算正确的是( )A、 B、 C、 D、3. 市直某中学足球队的18名队员的年龄情况如下表:年龄(单位:岁)
14
15
16
17
18
人数(单位:名)
3
6
4
4
1
则这些队员年龄的众数和中位数分别是( )
A、15,15 B、1,4 C、15,15.5 D、1,3.54. 下列说法错误的是( )A、过一点有且只有一条直线与已知直线平行 B、两条平行线的所有公垂线段都相等 C、平行于同一条直线的两条直线平行 D、垂线段最短5. 如图,DH∥EG∥BC,EF∥CD,则图中与∠1(不包括∠1)一定相等的角有( )个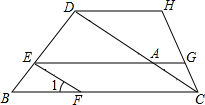 A、3 B、4 C、5 D、66. 常德市出租车的收费规定如下:出租车起步价所包含的路程为0~2km,超过2km的部分按每千米另收费.甲乘坐这种出租车走了8千米,付了12元;乙乘坐这种出租车走了13千米,付了17元.设该出租车的起步价为x元,超过2km后,每千米的车费是y元,根据题意,所列方程组正确的是( )A、 B、 C、 D、7. 如图是小明在镜子中看到的钟表的图象,此时的真实时间是( )
A、3 B、4 C、5 D、66. 常德市出租车的收费规定如下:出租车起步价所包含的路程为0~2km,超过2km的部分按每千米另收费.甲乘坐这种出租车走了8千米,付了12元;乙乘坐这种出租车走了13千米,付了17元.设该出租车的起步价为x元,超过2km后,每千米的车费是y元,根据题意,所列方程组正确的是( )A、 B、 C、 D、7. 如图是小明在镜子中看到的钟表的图象,此时的真实时间是( )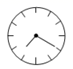 A、4:40 B、4:20 C、7:40 D、7:208. “抢30”游戏规则是:第一个人先说“1”或“1、2”,第二个人要接着按顺序往下说一个或两个数,然后又轮到第一个人,再接着按顺序往下说一个或两个数,这样两人反复轮流,每次每人说一个或两个数都可以,但是不可以连说三个数,谁先抢到30则获胜.那么采取适当策略,那么一定能取胜的是( )A、先报数者 B、后报数者 C、两者都可能 D、很难预料
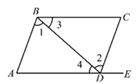
A、4:40 B、4:20 C、7:40 D、7:208. “抢30”游戏规则是:第一个人先说“1”或“1、2”,第二个人要接着按顺序往下说一个或两个数,然后又轮到第一个人,再接着按顺序往下说一个或两个数,这样两人反复轮流,每次每人说一个或两个数都可以,但是不可以连说三个数,谁先抢到30则获胜.那么采取适当策略,那么一定能取胜的是( )A、先报数者 B、后报数者 C、两者都可能 D、很难预料二、填空题
-
9. 计算:10. 已知 是方程组 的解,则 =11. 若 ,则12. 如图,给出下列条件:① ∠1=∠2;② ∠3=∠4;③ ∠A=∠CDE;④ ∠ABC+∠C=180∘.其中,能推出 AB∥CD 的条件是(填序号)
 13. 若方程组 的解中x与y的值相等,则k为 .14. 小明购买文具需要付32元,小明的钱包里只有2元和5元两种面值的若干张,无需找零钱,则他最多有种付款方式.15. 若 是完全平方公式,则m=16. 如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=°.
13. 若方程组 的解中x与y的值相等,则k为 .14. 小明购买文具需要付32元,小明的钱包里只有2元和5元两种面值的若干张,无需找零钱,则他最多有种付款方式.15. 若 是完全平方公式,则m=16. 如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=°. 17. 如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
17. 如图,已知AB∥CD,∠B=40°,CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数.
三、解答题
-
18. 解方程组(1)、(2)、19. 因式分解(1)、(2)、20. 化简求值: ,其中 .21. 某工厂第一季度生产甲、乙两种机器共450台,改进技术后,计划第二季度生产这两种机器520台,其中甲种机器增产10%,乙种机器增产20%,该厂第二季度计划生产甲、乙机器各多少台?22. 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O、M也在格点上.
 (1)、画出 关于直线OM对称的 ;
(1)、画出 关于直线OM对称的 ;画出 绕点O按顺时针方向旋转90°后所得的 ;
(2)、计算: 的面积为;(3)、 (填“>”,“=”或“<”)23. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环): (1)、根据表格中的数据,计算出甲的平均成绩是环,乙的平均成绩是环;(2)、分别计算甲、乙六次测试成绩的方差;(3)、根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.24. 如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90 .
(1)、根据表格中的数据,计算出甲的平均成绩是环,乙的平均成绩是环;(2)、分别计算甲、乙六次测试成绩的方差;(3)、根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.24. 如图,BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90 . (1)、求证:AB∥CD;(2)、若DG∥BE,试说明DG是∠CDF的平分线.25. 在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,通过用不同的方法求同一个平面图形的面积验证了平方差公式和完全平方公式,我们把这种方法称为等面积法.类似地,通过不同的方法求同一个立体图形的体积,我们称为等体积法;
(1)、求证:AB∥CD;(2)、若DG∥BE,试说明DG是∠CDF的平分线.25. 在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,通过用不同的方法求同一个平面图形的面积验证了平方差公式和完全平方公式,我们把这种方法称为等面积法.类似地,通过不同的方法求同一个立体图形的体积,我们称为等体积法;根据课堂学习的经验,解决下列问题:
在一个边长为a 的正方体中挖出一个边长为b的正方体(如图1),然后利用切割的方法把剩余的立体图形(如图2)分成三部分(如图3),这三部分长方体的体积依次为 , , .


 (1)、分解因式: ;(2)、请用两种不同的方法求图1中的立体图形的体积:(用含有 的代数式表示)
(1)、分解因式: ;(2)、请用两种不同的方法求图1中的立体图形的体积:(用含有 的代数式表示)①;
②;
思考:类比平方差公式,你能得到的等式为;
(3)、应用:利用在(2)中所得到的等式进行因式分解: ;(4)、拓展:已知 ,你能求出代数式 的值为 .