四川省自贡市2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2020-09-21 类型:期末考试
一、单选题
-
1. 的算术平方根是( )
A、3 B、 C、±3 D、±2. 为了反映某地的天气变化趋势,最好选择( )A、扇形统计图 B、条形统计图 C、折线统计图 D、以上三种都不行3. 如图,若 , 相交于点O,过点O作 ,则下列结论错误的是( )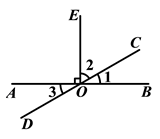 A、 与 互为余角 B、 与 互为余角 C、 与 互为补角 D、 与 是对顶角4. 以下调查中适合作抽样调查的有( )
A、 与 互为余角 B、 与 互为余角 C、 与 互为补角 D、 与 是对顶角4. 以下调查中适合作抽样调查的有( )①了解一批灯泡的使用寿命;②研究某种新式武器的威力;③审查一本书科学性的错误.④调查人们的环保意识.
A、4种 B、3种 C、2种 D、1种5. 将点P 向右平移1个单位长度到 ,且 在y轴上,那么点P的坐标是( )A、(1,3) B、(3,-1) C、(-1,5) D、(3,1)6. 下列方程中,与方程组 同解的是( )A、 B、 C、 D、7. 如图, ∥ , 为直线 上两点,且 平分 ;若 ,则∠2的度数为( )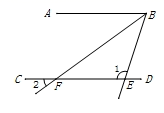 A、30° B、36° C、42° D、45°8. 若关于x的不等式组 只有4个整数解,则a的取值范围是( )A、 B、 C、 D、
A、30° B、36° C、42° D、45°8. 若关于x的不等式组 只有4个整数解,则a的取值范围是( )A、 B、 C、 D、二、填空题
-
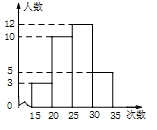
9. 如果 ,那么 等于 .10. 若 是方程 的解,则 = .11. 命题:同旁内角互补的题设是 , 结论是 .12. 某校为了了解七年级学生的体能情况,随机抽查了其中的30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,请根据图示计算,仰卧起坐次数在25~30次之间的频率是 .
 13. 如图,若满足条件 , 则有AB∥CD , 理由是 . (要求:不再添加辅助线,只需填一个答案即可)
13. 如图,若满足条件 , 则有AB∥CD , 理由是 . (要求:不再添加辅助线,只需填一个答案即可)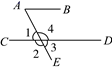 14. 已知点M(a , b)的坐标满足 ,且 ,则点N(1-a , b-1)在第象限.
14. 已知点M(a , b)的坐标满足 ,且 ,则点N(1-a , b-1)在第象限.三、解答题
-
15. 计算: .16. 解方程组:17. 解不等式组: 并在数轴上表示其解集.18. 已知:如图,在△ 中, 于点D,E是 上一点,且 .求证: .
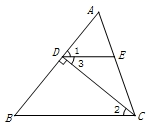
请在括号内填写出证明依据.
证明:∵ (已知)
∴ ()
∵ ()
∴ ()
∴ ∥ ()
∴ ()
19. 如图所示,大长方形图案由10个完全一样的小长方形拼成,若大长方形的短边长为 ,求图中每一个小长方形的面积.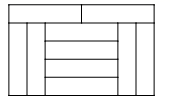 20. 已知△ABC中,点A(-1,2),B(-3,-2),C(3,-3),试解決下列问题:
20. 已知△ABC中,点A(-1,2),B(-3,-2),C(3,-3),试解決下列问题: (1)、在直角坐标系中画出△ABC.(2)、求△ABC的面积21. 某校七年级开展了为期一周的“敬老爱亲”社会实践活动,并根据做家务的时间来评价他们在活动中的表现,为了解活动开展情况,学校随机调查了本校七年级50名学生在这次活动中做家务的时间(学生做家务的时间在0.5至3小时之内),并将统计的时间(单位:小时)分成5组:A. ,B . ,C . ,D . ,E . .王老师根据他手机的数据,制成两幅不完整的统计图(如图).
(1)、在直角坐标系中画出△ABC.(2)、求△ABC的面积21. 某校七年级开展了为期一周的“敬老爱亲”社会实践活动,并根据做家务的时间来评价他们在活动中的表现,为了解活动开展情况,学校随机调查了本校七年级50名学生在这次活动中做家务的时间(学生做家务的时间在0.5至3小时之内),并将统计的时间(单位:小时)分成5组:A. ,B . ,C . ,D . ,E . .王老师根据他手机的数据,制成两幅不完整的统计图(如图).请根据图中提供的信息,解答下列问题:
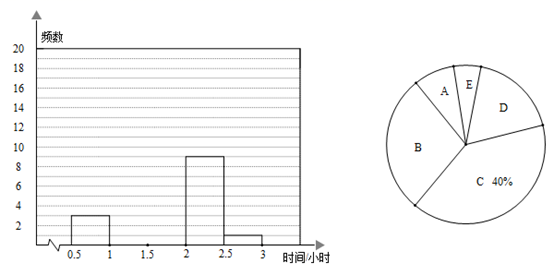 (1)、扇形统计图中D组扇形圆心角的度数是;(2)、补全频数分布直方图;(3)、该校七年级共有学生500名,请估计在这次活动中,七年级每周做家务时间为1至2小时的学生人数.22. 请阅读求绝对值不等式 和 的解集过程.
(1)、扇形统计图中D组扇形圆心角的度数是;(2)、补全频数分布直方图;(3)、该校七年级共有学生500名,请估计在这次活动中,七年级每周做家务时间为1至2小时的学生人数.22. 请阅读求绝对值不等式 和 的解集过程.对于绝对值不等式 ,从图1的数轴上看:大于-3而小于3的绝对值是是小于3的,所以 的解集为 ;
对于绝对值不等式 ,从图2的数轴上看:小于-3而大于3的绝对值是是大于3的,所以 的解集为 或 .
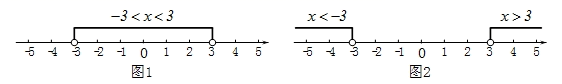
已知关于x、y的二元一次方程组 的解满足 ,其中m是负整数,求m的值.
23. 某商店销售 两种型号的皮箱,进价100元、80元,第一天卖出A型3个,B型2个,销售收入590元;第二天A型5个,B型4个,销售收入1050元.(1)、若商店准备用不多于5000元的金额再采购这两种型号的皮箱共55个,求A种型号的皮箱最多能采购多少个?(2)、在(1)的条件下,商店销售完这55个皮箱能否实现利润超过1380元的目标?若能,请给出相应的采购方案;若不能,请说明理由.24. 在平面直角坐标系中,点A , B在坐标轴上,其中 、 满足: .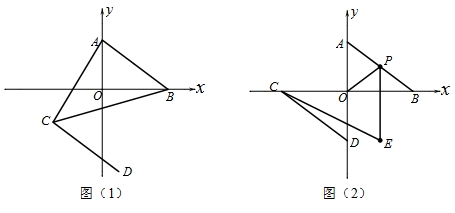 (1)、求A , B两点的坐标;(2)、将线段 平移至 ,点A对应点为 ,如图(1)所示,若三角形 的面积为14.5,求点D的坐标;(3)、平移线段 至 ,若点 也在坐标轴上,如图(2)所示,P为线段 上的一动点(不与A , B重合),连接 , 平分 , .求证: .
(1)、求A , B两点的坐标;(2)、将线段 平移至 ,点A对应点为 ,如图(1)所示,若三角形 的面积为14.5,求点D的坐标;(3)、平移线段 至 ,若点 也在坐标轴上,如图(2)所示,P为线段 上的一动点(不与A , B重合),连接 , 平分 , .求证: .