高中数学人教新课标A版 选修2-1 3.2立体几何中的向量方法
试卷更新日期:2020-09-21 类型:同步测试
一、单选题
-
1. 如图,在长方体 中,M,N分别是棱BB1 , B1C1的中点,若∠CMN=90°,则异面直线AD1和DM所成角为( )
 A、30° B、45° C、60° D、90°2. 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1= ,则AA1与平面AB1C1所成的角为( )
A、30° B、45° C、60° D、90°2. 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AC=2,AA1= ,则AA1与平面AB1C1所成的角为( ) A、 B、 C、 D、3. 已知两平面的法向量分别为 , ,则两平面所成的二面角为( )A、 B、 C、 或 D、4. 在四面体 中,已知棱 的长为 ,其余各棱长都为1,则二面角 的平面角的余弦值为( )A、 B、 C、 D、5. 正方体ABCD—A′B′C′D′中,AB的中点为M,DD′的中点为N,则异面直线B′M与CN所成角的大小为( )A、0° B、45° C、60 ° D、90°6. 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( )
A、 B、 C、 D、3. 已知两平面的法向量分别为 , ,则两平面所成的二面角为( )A、 B、 C、 或 D、4. 在四面体 中,已知棱 的长为 ,其余各棱长都为1,则二面角 的平面角的余弦值为( )A、 B、 C、 D、5. 正方体ABCD—A′B′C′D′中,AB的中点为M,DD′的中点为N,则异面直线B′M与CN所成角的大小为( )A、0° B、45° C、60 ° D、90°6. 如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,使得∠B′AC=60°.那么这个二面角大小是( ) A、30° B、60° C、90° D、120°7. 如图,直三棱柱 的底面是边长为6的等边三角形,侧棱长为2,E是棱BC上的动点,F是棱 上靠近 点的三分点,M是棱 上的动点,则二面角 的正切值不可能是( )
A、30° B、60° C、90° D、120°7. 如图,直三棱柱 的底面是边长为6的等边三角形,侧棱长为2,E是棱BC上的动点,F是棱 上靠近 点的三分点,M是棱 上的动点,则二面角 的正切值不可能是( ) A、 B、 C、 D、8. 如图,三棱柱 满足棱长都相等且 平面 ,D是棱 的中点,E是棱 上的动点.设 ,随着x增大,平面BDE与底面ABC所成锐二面角的平面角是( )
A、 B、 C、 D、8. 如图,三棱柱 满足棱长都相等且 平面 ,D是棱 的中点,E是棱 上的动点.设 ,随着x增大,平面BDE与底面ABC所成锐二面角的平面角是( ) A、先增大再减小 B、减小 C、增大 D、先减小再增大9. 如图,正四棱锥S-ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是( )
A、先增大再减小 B、减小 C、增大 D、先减小再增大9. 如图,正四棱锥S-ABCD中,O为顶点在底面内的投影,P为侧棱SD的中点,且SO=OD,则直线BC与平面PAC的夹角是( ) A、30° B、45° C、60° D、90°10. 已知正四面体 中, 为 的中点,则过点 与侧面 和底面 所在平面都成 的平面共有( )(注:若二面角 的大小为 ,则平面 与平面 所成的角也为 )A、1个 B、2个 C、3个 D、4个11. 如图,设矩形 ABCD 所在的平面与梯形 ACEF 所在平面交于 AC ,若 ,则下面二面角的平面角大小为定值的是( )
A、30° B、45° C、60° D、90°10. 已知正四面体 中, 为 的中点,则过点 与侧面 和底面 所在平面都成 的平面共有( )(注:若二面角 的大小为 ,则平面 与平面 所成的角也为 )A、1个 B、2个 C、3个 D、4个11. 如图,设矩形 ABCD 所在的平面与梯形 ACEF 所在平面交于 AC ,若 ,则下面二面角的平面角大小为定值的是( )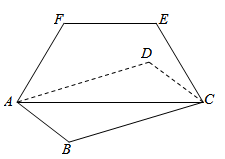 A、 B、 C、 D、12. 在三棱锥 中, , , P在平面 的射影O为 的中点,D是 上的动点,M,N是 的两个三等分点, ( ),记二面角 , 的平面角分别为 , .若 ,则 的最大值为( )A、 B、 C、 D、
A、 B、 C、 D、12. 在三棱锥 中, , , P在平面 的射影O为 的中点,D是 上的动点,M,N是 的两个三等分点, ( ),记二面角 , 的平面角分别为 , .若 ,则 的最大值为( )A、 B、 C、 D、二、填空题
-
13. 棱长相等的三棱锥的任意两个面组成的二面角的余弦值是 .14. 将边长为1的正方形 沿对角线 折叠,使得点B和D的距离为1,则二面角 的大小为.15. 如图,在正方体 中,直线 与平面 所成的角等于 .
 16. 四棱锥 中, 平面ABCD, , ,BC//AD,已知Q是四边形ABCD内部一点,且二面角 的平面角大小为 ,若动点Q的轨迹将ABCD分成面积为 的两部分,则 = .
16. 四棱锥 中, 平面ABCD, , ,BC//AD,已知Q是四边形ABCD内部一点,且二面角 的平面角大小为 ,若动点Q的轨迹将ABCD分成面积为 的两部分,则 = .三、解答题
-
17. 在三棱锥A—BCD中,已知CB=CD= ,BD=2,O为BD的中点,AO⊥平面BCD,AO=2,E为AC的中点.
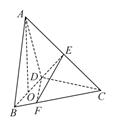 (1)、求直线AB与DE所成角的余弦值;(2)、若点F在BC上,满足BF= BC,设二面角F—DE—C的大小为θ,求sinθ的值.18. 如图,在直三棱柱 中,已知 , , , .D是线段 的中点.
(1)、求直线AB与DE所成角的余弦值;(2)、若点F在BC上,满足BF= BC,设二面角F—DE—C的大小为θ,求sinθ的值.18. 如图,在直三棱柱 中,已知 , , , .D是线段 的中点. (1)、求直线 与平面 所成角的正弦值;(2)、求二面角 的大小的余弦值.19. 如图,在三棱柱 中, 平面 , ,且 .
(1)、求直线 与平面 所成角的正弦值;(2)、求二面角 的大小的余弦值.19. 如图,在三棱柱 中, 平面 , ,且 . (1)、求棱 与 所成的角的大小;(2)、在棱 上确定一点 ,使二面角 的平面角的余弦值为 .20. 如图,在直三棱柱 中, , , , .
(1)、求棱 与 所成的角的大小;(2)、在棱 上确定一点 ,使二面角 的平面角的余弦值为 .20. 如图,在直三棱柱 中, , , , . (1)、设 ,异面直线 与 所成角的余弦值为 ,求 的值;(2)、若点D是 的中点,求二面角 的余弦值.
(1)、设 ,异面直线 与 所成角的余弦值为 ,求 的值;(2)、若点D是 的中点,求二面角 的余弦值.

