初中数学苏科版七年级上册3.3 代数式的值同步练习

试卷更新日期：2020-09-18 类型：同步测试

进入出卷网下载

一、单选题

1. 当 $x = - 2$ 时，代数式 $x+ 3$ 的值是（）

A、1 B、－1 C、5 D、－5

查看试题解析
2. 若多项式3x²－5x＋6的值为12，则多项式6x²－10x＋6的值为（）

A、14 B、16 C、20 D、18

查看试题解析
3. 若|a﹣1|+|b﹣2|=0，那么2ab=（　　）

A、-4 B、+4 C、-8 D、+8

查看试题解析
4. 若a²=25，|bl=3，则a+b=（）

A、-8 B、±8 C、±2 D、±8或±2

查看试题解析
5. 当x=1时，代数式ax³-3bx+5的值是2019，则当x=-1时，这个代数式的值是（）

A、2014 B、-2019 C、2009 D、-2009

查看试题解析
6. 按如图所示的运算程序，输出 $y$ 的值为 $11$ 的是（）

A、 $x = - 3$ B、 $x = 0$ C、 $x = 5$ D、 $x = - 1$

查看试题解析
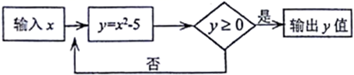7. 按如图所示的程序运算：当输入的数据为1时，则输出的数据是（）

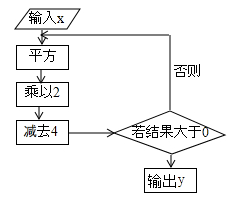A、2 B、4 C、6 D、8

查看试题解析
8. 已知代数式x﹣2y的值是5，则代数式﹣3x+6y+1的值是（）

A、16 B、﹣14 C、14 D、﹣16

查看试题解析
9. 若a ， b互为相反数，c ， d互为倒数，m的绝对值是1，n是有理数且既不是正数也不是负数，则2014^a^+b+1+m²-（cd）²⁰¹⁴+n（a+b+c+d）的值为（　　）

A、1 B、-1 C、0 D、2014

查看试题解析
10. 历史上，数学家欧拉最先把关于x的多项式用记号f（x）来表示，把x等于某数a时的多项式的值用f（a）来表示，例如x=﹣1时，多项式f（x）=x²+2x﹣3的值记为f（﹣1），那么f（﹣1）等于（）

A、0 B、﹣4 C、﹣6 D、6

查看试题解析

二、填空题

11. 已知 $a + b = \frac{1}{2}$ ，则代数式 $2 a + 2 b - 3$ 的值为.

查看试题解析
12. 已知代数式 $x^{2} - \frac{3}{2} x$ 的值为10，则 $2 x^{2} - 3 x + 2000$ 的值为．

查看试题解析
13. 如图所示是一个设计好的计算程序，若输入x的值为1，那么执行此程序后，输出的数y是.

查看试题解析
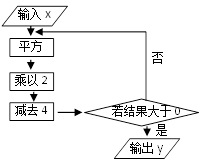14. 已知：当x=-2时，代数式 $a x^{3} + b x + 5$ 的值为 $- 9$ ，那么当x=2时, 代数式 $a x^{3} + b x + 5$ 的值为.

查看试题解析
15. 若多项式2x²+3x+7的值为10，则多项式6x²+9x-7的值为．

查看试题解析
16. 已知代数式 $x - 2 y$ 的值是1，则代数式 $3 - 2 x + 4 y$ 的值是.

查看试题解析

三、计算题

17. 当a=6，b $= - \frac{2}{3}$ 时，求下列代数式的值.

(1)、2ab；

(2)、a²+2ab+b².

查看试题解析
18. 已知|a-1|=3，|b-3|与（c+1）²互为相反数，且a＞b，求代数式2a-b+c-abc的值。

查看试题解析
19. 按下列程序计算，把答案写在表格内：

(1)、填写表格：

输入n

3

1

﹣2

﹣3

…

答案

12

…

(2)、请将题中计算程序用含n的代数式表示出来，并将该式化简.

查看试题解析
20.

(1)、当 $a = 3$ ， $b = 2$ 时，分别求代数式 $a^{2} - 2 a b + b^{2}$ 与 ${(a - b)}^{2}$ 的值；

(2)、当 $a = - 3$ ， $b = 1$ 时，分别求代数式 $a^{2} - 2 a b + b^{2}$ 与 ${(a - b)}^{2}$ 的值；

(3)、从（1），（2）中你发现了什么规律?利用你的发现，求当 $a = - \frac{2019}{2020}$ ， $b = \frac{1011}{2020}$ 时代数式 $a^{2} - 2 a b + b^{2}$ 的值.

查看试题解析
21. 如图，将面积为 $a^{2}$ 的小正方形和面积为 $b^{2}$ 的大正方形放在同一水平面上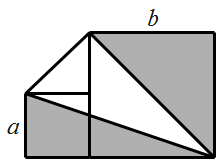（ $b > a > 0$ ）

(1)、用a、b表示阴影部分的面积；

(2)、计算当 $a = 3$ ， $b = 5$ 时，阴影部分的面积．

查看试题解析
22. 初一年级学生在7名教师的带领下去公园秋游，公园的门票为每人20元．现有两种优惠方案，甲方案：带队教师免费，学生按8折收费；乙方案：师生都7.5折收费．

(1)、若有m名学生，用代数式表示两种优惠方案各需多少元？

(2)、当m=50时，采用哪种方案优惠？

(3)、当m=400时，采用哪种方案优惠？

查看试题解析
23. 阅读下面的文字，完成后面的问题：
我们知道： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$
那么

(1)、 $\frac{1}{4 \times 5} =$ ； $\frac{1}{21 \times 22} =$ ；

(2)、用含有 $n$ 的等式表示你发现的规律；

(3)、如果 $| a - 1 | + {(a b - 2)}^{2} = 0$ ，求 $\frac{1}{a b} + \frac{1}{(a + 1) (b + 1)} + \frac{1}{(a + 2) (b + 2)} + ... + \frac{1}{(a + 2016) (b + 2017)}$ 的值.

查看试题解析
24. 历史上杰出的数学家欧拉最先把关于 $x$ 的多项式用记号 $f (x)$ （ $f$ 可用其它字母，但不同的字母表示不同的多项式）形式来表示，例如 $f (x) = x^{2} - 2 x + 4$ ，其意义是当 $x = a$ 时多项式的值用 $f (a)$ 来表示．例如 $x = 2$ 时，多项式 $x^{2} - 2 x + 4$ 的值记为 $f (2) = 2^{2} - 2 \times 2 + 4 = 4$ ．已知 $g (x) = - 2 x^{2} + 5 x - 1$ ，
$h (x) = a x^{3} + 2 a x^{2} - x - 8$ ．

(1)、求 $g (- 2)$ 值；

(2)、若 $h (\frac{1}{2}) = - 11$ ，求 $g (\frac{1}{a}) \cdot h (2)$ 的值．

查看试题解析
25. 已知（2x﹣1）⁵=a₅x⁵+a₄x⁴+a₃x³+a₂x²+a₁x+a₀对于任意的x都成立.求：

(1)、a₀的值；

(2)、a₀_﹣a₁+a₂﹣a₃+a₄﹣a₅的值；

(3)、a₂+a₄的值.

查看试题解析

输入n	3	1	﹣2	﹣3	…
答案	12				…

初中数学苏科版七年级上册3.3 代数式的值 同步练习

一、单选题

二、填空题

三、计算题

初中数学苏科版七年级上册3.3 代数式的值同步练习