初中数学华师大版九年级上学期第24章测试卷

试卷更新日期：2020-09-18 类型：单元试卷

进入出卷网下载

一、单选题

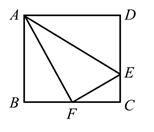
1. 如图，路灯距地面8米，身高1.6米的小明从距离路灯的底部(点O)20米的点A处沿OA所在的直线行走14米到点B时，人影长度（）

A、变长3.5米 B、变长2.5米 C、变短3.5米 D、变短2.5米

查看试题解析
2. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，D是 $A B$ 的中点， $B E ⊥ C D$ ，交 $C D$ 的延长线于点E ．若 $A C = 2$ ， $B C = 2 \sqrt{2}$ ，则 $B E$ 的长为（）

A、 $\frac{2 \sqrt{6}}{3}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
3. 如图，在Rt△ABC中，∠ACB=90°，CD为中线，延长CB至点E，使BE=BC，连结DE，F为DE中点，连结BF.若AC=8，BC=6，则BF的长为（）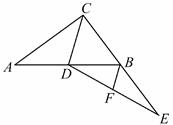

A、2 B、2.5 C、3 D、4

查看试题解析
4. 在Rt△ABC中，∠C=90°，BC=5，AC=12，则sinB的值是（）

A、 $\frac{5}{12}$ B、 $\frac{12}{5}$ C、 $\frac{5}{13}$ D、 $\frac{12}{13}$

查看试题解析
5. 如图，在 $R t △ A C B$ 中， $∠ C = 90 ° ， s i n B = 0.5$ ，若 $A C = 6$ ，则 $B C$ 的长为（）

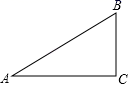A、8 B、12 C、 $6 \sqrt{3}$ D、 $12 \sqrt{3}$

查看试题解析
6. 如图，为了测量一条河流的宽度，一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置，T在P的正北方向，且T在Q的北偏西70°方向，则河宽（PT的长）可以表示为（）

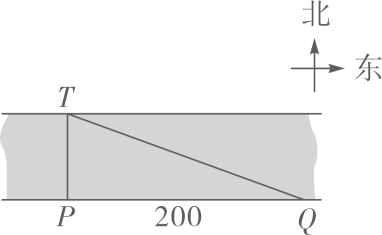A、200tan70°米 B、 $\frac{200}{\tan 70 °}$ 米 C、200sin70°米 D、 $\frac{200}{\sin 70 °}$ 米

查看试题解析

二、计算题

7. 先化简，再求代数式的值： $(\frac{4 x}{x - 2} - \frac{x}{x + 2}) \div \frac{x}{x^{2} - 4}$ ，其中 $x = \cos 60 ° + 6^{- 1}$ .

查看试题解析
8. 计算： $2 \sin 60^{°} + {(- \frac{1}{3})}^{- 2} + {(π - 2020)}^{0} + | 2 - \sqrt{3} |$

查看试题解析
9. 先化简，再求代数式 $(1 - \frac{2}{x + 1}) \div \frac{x^{2} - 1}{2 x + 2}$ 的值，其中 $x = 4 \cos 30 ° - 1$

查看试题解析

三、解答题

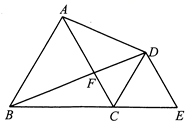
10. 如图，要测量河宽，可在两岸找到相对的两点A、B，先从B出发与AB成90°方向向前走50米，到C处立一标杆，然后方向不变继续朝前走10米到D处，在D处转90°，沿DE方向走到E处，若A、C、E三点恰好在同一直线上，且DE=17米，你能根据题目提供的数据和图形求出河宽吗？

查看试题解析
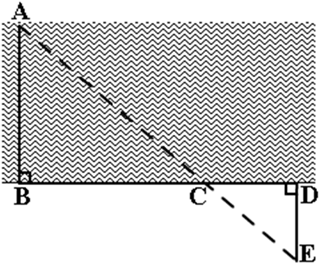11. 如图，某中学两座教学楼中间有个路灯，甲、乙两个人分别在楼上观察路灯顶端，视线所及如图①所示。根据实际情况画出平面图形如图②，CD⊥DF，AB⊥DF，EF⊥DF，甲从点C可以看到点G处，乙从点E恰巧可以看到点D处，点B是DF的中点，路灯AB高5.5米，DF=120米，BG=10.5米，求甲、乙两人的观测点到地面的距离的差。

查看试题解析
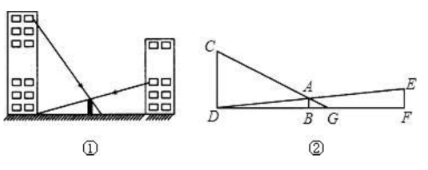12. 某数学兴趣小组去测量一座小山的高度，在小山顶上有一高度为20米的发射塔 $A B$ ，如图所示，在山脚平地上的D处测得塔底B的仰角为 $30 °$ ，向小山前进80米到达点E处，测得塔顶A的仰角为 $60 °$ ，求小山 $B C$ 的高度．

查看试题解析
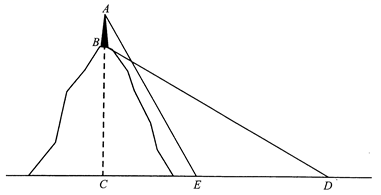13. 如图， $C$ 处是一钻井平台，位于东营港口A的北偏东 $60^{\circ}$ 方向上，与港口A相距 $60 \sqrt{2}$ 海里，一艘摩托艇从A出发，自西向东航行至B时，改变航向以每小时50海里的速度沿 $B C$ 方向行进，此时C位于B的北偏西 $45^{\circ}$ 方向，则从B到达C需要多少小时？

查看试题解析
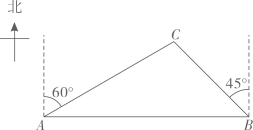14. 如图，在一笔直的海岸线上有A，B两个观测站，A在B的正西方向，AB=2km，从观测站A测得船C在北偏东45°的方向，从观测站B测得船C在北偏西30°的方向.求船C离观测站A的距离.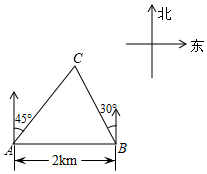

查看试题解析

四、综合题

15. 如图， $△ A B C$ 和 $△ C D E$ 都是等边三角形，点B、C、E三点在同一直线上，连接 $B D$ ， $A D$ ， $B D$ 交 $A C$ 于点F．

(1)、若 $A D^{2} = D F \cdot D B$ ，求证： $A D = B F$ ；

(2)、若 $∠ B A D = 90 °$ ， $B E = 6$ ．
①求 $\tan ∠ D B E$ 的值；

②求 $D F$ 的长．

查看试题解析
16. 在矩形ABCD中，E为 $D C$ 上的一点，把 $Δ A D E$ 沿AE翻折，使点D恰好落在BC边上的点F．

(1)、求证： $Δ A B F \sim Δ F C E$

(2)、若 $A B = 2 \sqrt{3} ， A D = 4$ ，求EC的长；

(3)、若 $A E - D E = 2 E C$ ，记 $∠ B A F = α ， ∠ F A E = β$ ，求 $\tan α + \tan β$ 的值．

查看试题解析

初中数学华师大版九年级上学期 第24章测试卷

一、单选题

二、计算题

三、解答题

四、综合题

初中数学华师大版九年级上学期第24章测试卷