初中数学华师大版九年级上学期 第24章 24.4解直角三角形
试卷更新日期:2020-09-18 类型:同步测试
一、单选题
-
1. 从一艘船上测得海岸上高为42米的灯塔顶部的仰角是30度,船离灯塔的水平距离为( )A、 米 B、 米 C、21米 D、42米2. 如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比)i=1:2.4,则信号塔AB的高度约为( )
(参考数据:sin43°≈0.68,cos43°≈0.73,tan43°≈0.93)
 A、23米 B、24米 C、24.5米 D、25米3. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、23米 B、24米 C、24.5米 D、25米3. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )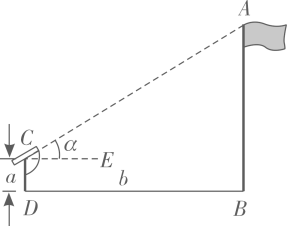 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
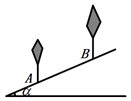
4. 如图,为了了解山坡上两棵树间的水平距离,数学活动小组的同学们测得该山坡的倾斜角 ,两树间的坡面距离 ,则这两棵树的水平距离约为m(结果精确到 ,参考数据: ).
 5. 如图,航拍无人机从A处测得一幢建筑物顶部C的仰角是30°,测得底部B的俯角是60° ,此时无人机与该建筑物的水平距离AD是9米,那么该建筑物的高度BC为米(结果保留根号).
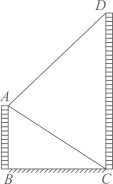
5. 如图,航拍无人机从A处测得一幢建筑物顶部C的仰角是30°,测得底部B的俯角是60° ,此时无人机与该建筑物的水平距离AD是9米,那么该建筑物的高度BC为米(结果保留根号). 6. 如图,我市在建高铁的某段路基横断面为梯形 , ∥ , 长为6米,坡角 为45°, 的坡角 为30°,则 的长为 米 (结果保留根号)
6. 如图,我市在建高铁的某段路基横断面为梯形 , ∥ , 长为6米,坡角 为45°, 的坡角 为30°,则 的长为 米 (结果保留根号)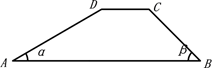
三、解答题
-
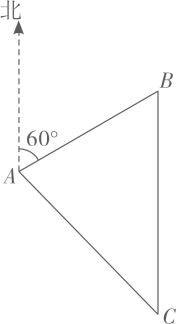
7. 如图,某海岸边有B,C两码头,C码头位于B码头的正东方向,距B码头40海里.甲、乙两船同时从A岛出发,甲船向位于A岛正北方向的B码头航行,乙船向位于A岛北偏东 方向的C码头航行,当甲船到达距B码头30海里的E处时,乙船位于甲船北偏东 方向的D处,求此时乙船与C码头之间的距离.(结果保留根号)
 8. 居家学习期间,小睛同学运用所学知识在自家阳台测对面大楼的高度如图,她利用自制的测角仪测得该大楼顶部的仰角为 ,底部的俯角为 :又用绳子测得测角仪距地面的高度 为 .求该大棱的高度(结果精确到 )(参考数据: , , )
8. 居家学习期间,小睛同学运用所学知识在自家阳台测对面大楼的高度如图,她利用自制的测角仪测得该大楼顶部的仰角为 ,底部的俯角为 :又用绳子测得测角仪距地面的高度 为 .求该大棱的高度(结果精确到 )(参考数据: , , ) 9. 从A处看一栋楼顶部的仰角为 ,看这栋楼底部的俯角为 ,A处与楼的水平距离 为 ,若 ,求这栋楼高.
9. 从A处看一栋楼顶部的仰角为 ,看这栋楼底部的俯角为 ,A处与楼的水平距离 为 ,若 ,求这栋楼高.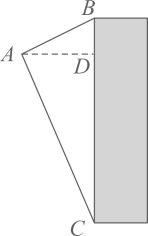
四、综合题
-
10. 如图,小明利用学到的数学知识测量大桥主架在水面以上的高度 ,在观测点 处测得大桥主架顶端 的仰角为30°,测得大桥主架与水面交汇点 的俯角为14°,观测点与大桥主架的水平距离 为60米,且 垂直于桥面.(点 在同一平面内)

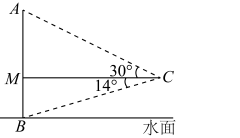
(参考数据 )
(1)、求大桥主架在桥面以上的高度AM;(结果保留根号)(2)、求大桥主架在水面以上的高度 .(结果精确到1米)