初中数学华师大版九年级上学期 第24章 24.2 直角三角形的性质
试卷更新日期:2020-09-18 类型:同步测试
一、单选题
-
1. 长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A、4 B、5 C、6 D、72. 如图,在正方形 中,点P是 上一动点(不与 重合) ,对角线 相交于点O,过点P分别作 的垂线,分别交 于点 交 于点 .下列结论:① ;② ;③ ;④ ;⑤点O在 两点的连线上.其中正确的是( )
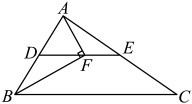
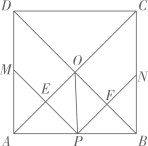 A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤3. 如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( )
A、①②③④ B、①②③⑤ C、①②③④⑤ D、③④⑤3. 如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点连接AF,BF,∠AFB =90°,且AB=8,BC= 14,则EF的长是 ( )
 A、2 B、3 C、4 D、54. 如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )
A、2 B、3 C、4 D、54. 如图,在▱ABCD中,AB=5,BC=8.E是边BC的中点,F是▱ABCD内一点,且∠BFC=90°.连接AF并延长,交CD于点G.若EF∥AB,则DG的长为( )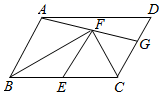 A、 B、 C、3 D、25. 如图,在 中, ,点H、E、F分别是边 、 、 的中点,若 ,则 的值为( )
A、 B、 C、3 D、25. 如图,在 中, ,点H、E、F分别是边 、 、 的中点,若 ,则 的值为( )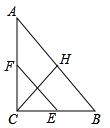 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
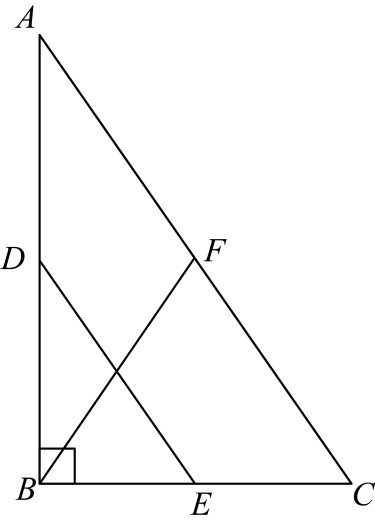
6. 已知直角三角形斜边长为16,则这个直角三角形斜边上的中线长为.7. 如图,在 中, , 、 、 分别为 、 、 的中点,若 ,则 .
 8. 如图,四边形ABCD中,AB∥CD,∠ABC=60°,AD=BC=CD=4,点M是四边形ABCD内的一个动点,满足∠AMD=90°,则点M到直线BC的距离的最小值为 .
8. 如图,四边形ABCD中,AB∥CD,∠ABC=60°,AD=BC=CD=4,点M是四边形ABCD内的一个动点,满足∠AMD=90°,则点M到直线BC的距离的最小值为 .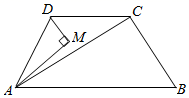 9. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为.
9. 如图,在△ABC中,AB=AC,∠BAC的平分线AD交BC于点D,E为AB的中点,若BC=12,AD=8,则DE的长为. 10. 如图,在菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于.
10. 如图,在菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为32,则OH的长等于.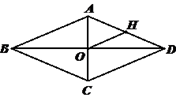
三、解答题
-
11. 如图,等腰△ABC,AB=AC,∠C=30°,AB⊥AD,AD=2,求BC的长.
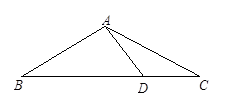 12. 如图所示,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB的高.
12. 如图所示,测量旗杆AB的高度时,先在地面上选择一点C,使∠ACB=15°.然后朝着旗杆方向前进到点D,测得∠ADB=30°,量得CD=13 m,求旗杆AB的高.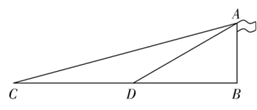
四、综合题
-
13. (教材呈现)下图是华师版九年级上册数学教材第103—104页的部分内容.
 (1)、定理证明:请根据教材图24.2.2的提示,结合图①完成直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”的证明.
(1)、定理证明:请根据教材图24.2.2的提示,结合图①完成直角三角形的性质:“直角三角形斜边上的中线等于斜边的一半”的证明.
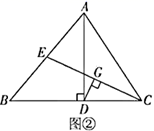
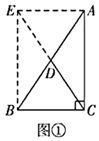 (2)、定理应用:如图②,在 中, ,垂足为点D(点D在 上), 是 边上的中线, 垂直平分 .求证: .
(2)、定理应用:如图②,在 中, ,垂足为点D(点D在 上), 是 边上的中线, 垂直平分 .求证: .