初中数学苏科版八年级上册2.2 轴对称的性质 同步练习
试卷更新日期:2020-09-18 类型:同步测试
一、单选题
-
1. 下列说法错误的是( )A、关于某直线成轴对称的两个图形一定能完全重合 B、线段是轴对称图形 C、全等的两个三角形一定关于某直线成轴对称 D、轴对称图形的对称轴至少有一条2. 如图,△ABC和△A′B′C′关于直线L对称,下列结论中符合题意的有( )
⑴△ABC≌△A′B′C′
⑵∠BAC=∠B′A′C′
⑶直线L垂直平分CC′
⑷直线BC和B′C′的交点不一定在直线L上.
 A、4个 B、3个 C、2个 D、1个3. 将一长方形纸片,按右图的方式折叠,BC,BD为折痕,则∠CBD的度数为( )
A、4个 B、3个 C、2个 D、1个3. 将一长方形纸片,按右图的方式折叠,BC,BD为折痕,则∠CBD的度数为( ) A、60° B、75° C、90° D、95°4. 如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD折叠后,若点C恰好落在AB边上的点E处,则△ADE的周长为( )
A、60° B、75° C、90° D、95°4. 如图,在△ABC中,AB=8,BC=6,AC=5,点D在AC上,连结BD,将△ABC沿BD折叠后,若点C恰好落在AB边上的点E处,则△ADE的周长为( ) A、5 B、6 C、7 D、85. 如图,把一个正方形经过上折、右折、下方折三次对折后沿虚线剪下,则所得图形是( )
A、5 B、6 C、7 D、85. 如图,把一个正方形经过上折、右折、下方折三次对折后沿虚线剪下,则所得图形是( )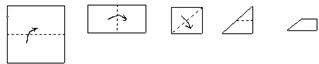 A、
A、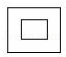 B、
B、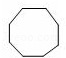 C、
C、 D、
D、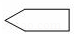 6. 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( )
6. 如图,在△ABC中,∠C=40°,将△ABC沿着直线l折叠,点C落在点D的位置,则∠1-∠2的度数是( ) A、40° B、80° C、90° D、140°7. 如图,把一长方形纸片ABCD沿EG折叠后,点A,B分别落在A′、B′的位置上,EA′与BC相交于点F,已知∠1=130°,则∠2的度数是( )
A、40° B、80° C、90° D、140°7. 如图,把一长方形纸片ABCD沿EG折叠后,点A,B分别落在A′、B′的位置上,EA′与BC相交于点F,已知∠1=130°,则∠2的度数是( )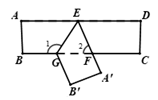 A、40° B、50° C、65° D、80°8. 如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画( )条线段.
A、40° B、50° C、65° D、80°8. 如图,方格纸上有2条线段,请你再画1条线段,使图中的3条线段组成一个轴对称图形,最多能画( )条线段.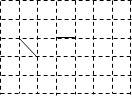 A、1 B、2 C、3 D、49. 如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )
A、1 B、2 C、3 D、49. 如图,图1是AD∥BC的一张纸条,按图1→图2→图3,把这一纸条先沿EF折叠并压平,再沿BF折叠并压平,若图3中∠CFE=18°,则图2中∠AEF的度数为( )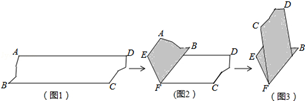 A、120° B、108° C、126° D、114°10. 如图,在四边形 ABCD 中,∠C=70°,∠B=∠D=90°,E、F 分别是 BC、DC 上的点,当△AEF 的周长最小时,∠EAF 的度数为( )
A、120° B、108° C、126° D、114°10. 如图,在四边形 ABCD 中,∠C=70°,∠B=∠D=90°,E、F 分别是 BC、DC 上的点,当△AEF 的周长最小时,∠EAF 的度数为( )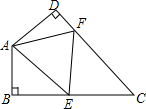 A、30° B、40° C、50° D、70°
A、30° B、40° C、50° D、70°二、填空题
-
11. 如图, 是一个三角形纸片,其中 , ,沿 折叠纸片,使点 落在点 处,则 .
 12. 将一个矩形纸片沿 折叠成如图所示的图形,若 ,则 的度数为 .
12. 将一个矩形纸片沿 折叠成如图所示的图形,若 ,则 的度数为 .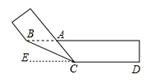 13. 如图,点 、 分别在 的 、 边上,沿 将 翻折,点 的对应点为点 , , ,且 ,则 等于(用含 、 的式子表示).
13. 如图,点 、 分别在 的 、 边上,沿 将 翻折,点 的对应点为点 , , ,且 ,则 等于(用含 、 的式子表示).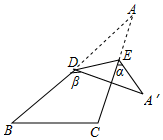 14. 如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为.
14. 如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为.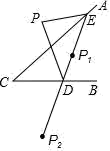 15. 如图,等边 的边长为 ,D、E分别是 、 上的点,将 沿直线 折叠,点A落在点F处,且点F在 外部,则阴影部分图形的周长为cm.
15. 如图,等边 的边长为 ,D、E分别是 、 上的点,将 沿直线 折叠,点A落在点F处,且点F在 外部,则阴影部分图形的周长为cm.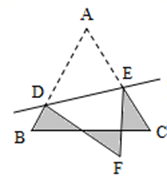 16. 如图,△ABC的内部有一点P,且D,E,F是P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠ADB+∠BEC+∠CFA=°.
16. 如图,△ABC的内部有一点P,且D,E,F是P分别以AB,BC,AC为对称轴的对称点.若△ABC的内角∠BAC=70°,∠ABC=60°,∠ACB=50°,则∠ADB+∠BEC+∠CFA=°.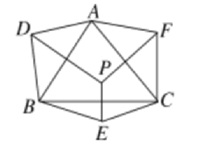 17. 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为 .
17. 如图,在△ABC中,将∠C沿DE折叠,使顶点C落在△ABC内C′处,若∠A=75°,∠B=65°,∠1=40°,则∠2的度数为 .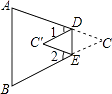 18.
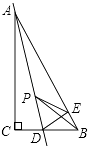
18.如图,在Rt△ABC中,∠C=90°,AB=5,AC=4,CB=3,点D是BC边上的点,将△ADC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
 19. 如图,在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按如图的方式折叠,若EF的长度为a,则△DEF的周长为(用含a的式子表示).
19. 如图,在三角形纸片ABC中,∠C=90°,∠B=30°,点D(不与B,C重合)是BC上任意一点,将此三角形纸片按如图的方式折叠,若EF的长度为a,则△DEF的周长为(用含a的式子表示).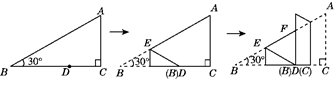 20. 如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1 , 再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2 , 依次折叠,则BDn= .
20. 如图,△ABC是边长为1的等边三角形,BD为AC边上的高,将△ABC折叠,使点B与点D重合,折痕EF交BD于点D1 , 再将△BEF折叠,使点B于点D1重合,折痕GH交BD1于点D2 , 依次折叠,则BDn= .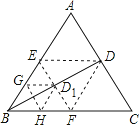
三、综合题
-
21. 作出已知图形△ABC 关于给定直线 l 的对称图形△A'B'C'.
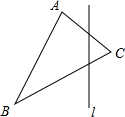 22. 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
22. 如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长. 23. 探索归纳:
23. 探索归纳: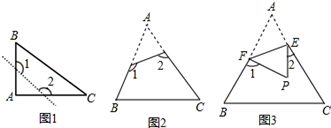 (1)、如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于;(2)、如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=;(3)、如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是;(4)、如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.24. 如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1 , P2是点P关于AB、AC的对称点,连结P1P2 , 分别交AB、AC于点D、E.
(1)、如图1,已知△ABC为直角三角形,∠A=90°,若沿图中虚线剪去∠A,则∠1+∠2等于;(2)、如图2,已知△ABC中,∠A=40°,剪去∠A后成四边形,则∠1+∠2=;(3)、如图2,根据(1)与(2)的求解过程,请你归纳猜想∠1+∠2与∠A的关系是;(4)、如图3,若没有剪掉,而是把它折成如图3形状,试探究∠1+∠2与∠A的关系并说明理由.24. 如图1,在△ABC中,∠A<90°,P是BC边上的一点,P1 , P2是点P关于AB、AC的对称点,连结P1P2 , 分别交AB、AC于点D、E.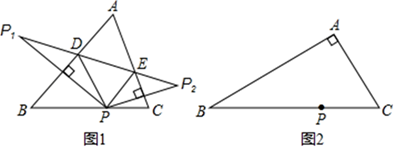 (1)、若∠A=52°,求∠DPE的度数;(2)、如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2 , (不写作法,保留作图痕迹),试判断点P1 , P2与点A是否在同一直线上,并说明理由.25. ABCD是长方形纸片的四个顶点,点E、F、H分别是边AB、BC、AD上的三点,连结EF、FH.
(1)、若∠A=52°,求∠DPE的度数;(2)、如图2,在△ABC中,若∠BAC=90°,用三角板作出点P关于AB、AC的对称点P1、P2 , (不写作法,保留作图痕迹),试判断点P1 , P2与点A是否在同一直线上,并说明理由.25. ABCD是长方形纸片的四个顶点,点E、F、H分别是边AB、BC、AD上的三点,连结EF、FH. (1)、将长方形纸片的ABCD按如图①所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′,点B′在F C′上,则∠EFH的度数为;
(1)、将长方形纸片的ABCD按如图①所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′,点B′在F C′上,则∠EFH的度数为;
(2)、将长方形纸片的ABCD按如图②所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′(B′、C′的位置如图所示),若∠B′FC′=18°,求∠EFH的度数;
(3)、将长方形纸片的ABCD按如图③所示的方式折叠,FE、FH为折痕,点B、C、D折叠后的对应点分别为B′、C′、D′(B′、C′的位置如图所示),若∠EFH=β°,求∠B′FC′的度数为 .
26. 如图 (1)、如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,
(1)、如图1,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,①写出图中一对全等的三角形,并写出它们的所有对应角;
②设 的度数为x , ∠ 的度数为y,那么∠1,∠2的度数分别是多少?(用含有x或y的代数式表示)
③∠A与∠1、∠2之间有一种数量关系始终保持不变,请找出这个规律.
(2)、如图2,把△ABC纸片沿DE折叠,当点A落在四边形BCDE外部时,∠A与∠1、∠2的数量关系是否发生变化?如果发生变化,求出∠A与∠1、∠2的数量关系;如果不发生变化,请说明理由.