初中数学苏科版八年级上册2.5等腰三角形的轴对称性 同步练习
试卷更新日期:2020-09-17 类型:同步测试
一、单选题
-
1. 下列说法正确是( )A、等腰三角形的角平分线、中线和高三线重合 B、等角对等边 C、等腰三角形一定是锐角三角形 D、等腰三角形两个底角相等2. 若等腰三角形的一个内角为92°,则它的顶角的度数为( )A、92° B、88° C、44° D、88°或44°3. 已知等腰三角形的一边长为3,另一边长为6,则这个等腰三角形的周长为( )A、12 B、12或15 C、15 D、94. 等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )A、70° B、20° C、70°或20° D、40°或140°5. 如图,在6×6的正方形网格中,点A , B均在正方形格点上,若在网格中的格点上找一点C , 使△ABC为等腰三角形,这样的点C一共有( )
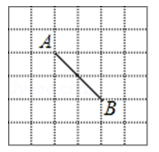
A、7个 B、8个 C、10个 D、12个6. 如图,AD=BC=BA,那么∠1与∠2之间的关系是( ) A、∠1=2∠2 B、2∠1+∠2=180° C、∠1+3∠2=180° D、3∠1﹣∠2=180°7. 如图,在△ABC中,点D是BC边上一点,AD=AC,过点D作DE⊥BC交AB于E,若△ADE是等腰三角形,则下列判断中正确的是( )
A、∠1=2∠2 B、2∠1+∠2=180° C、∠1+3∠2=180° D、3∠1﹣∠2=180°7. 如图,在△ABC中,点D是BC边上一点,AD=AC,过点D作DE⊥BC交AB于E,若△ADE是等腰三角形,则下列判断中正确的是( ) A、∠B=∠CAD B、∠BED=∠CAD C、∠ADB=∠AED D、∠BED=∠ADC8. 如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )
A、∠B=∠CAD B、∠BED=∠CAD C、∠ADB=∠AED D、∠BED=∠ADC8. 如图,∠ABC,∠ACB的平分线相交于点F,过点F作DE∥BC,交AB于D,交AC于E,那么下列结论正确的是:①△BDF,△CEF都是等腰三角形;②DE=BD+CE;③△ADE的周长为AB+AC;④BD=CE.( )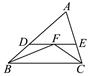 A、③④ B、①② C、①②③ D、②③④9. 如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )
A、③④ B、①② C、①②③ D、②③④9. 如图,在△ABC中,AB=AC,AD、CE是△ABC的两条中线,P是AD上一个动点,则下列线段的长度等于BP+EP最小值的是( )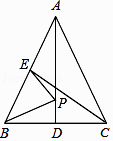 A、BC B、CE C、AD D、AC10. 如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( )
A、BC B、CE C、AD D、AC10. 如图,在△ABC中,∠A为钝角,AB=20cm,AC=12cm,点P从点B出发以3cm/s的速度向点A运动,点Q同时从点A出发以2cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动.当△APQ是等腰三角形时,运动的时间是( ) A、2.5s B、3s C、3.5s D、4s
A、2.5s B、3s C、3.5s D、4s二、填空题
-
11. 已知等腰三角形一腰上的高与另一腰的夹角为60°,则这个等腰三角形的顶角是 .12. 如图△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠EDF=.
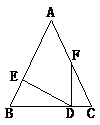 13. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=度.
13. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=度. 14. 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=s时,△POQ是等腰三角形.
14. 如图,∠BOC=60°,点A是BO延长线上的一点,OA=10cm,动点P从点A出发沿AB以2cm/s的速度移动,动点Q从点O出发沿OC以1cm/s的速度移动,如果点P、Q同时出发,用t(s)表示移动的时间,当t=s时,△POQ是等腰三角形.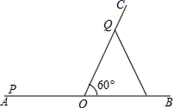 15. 如图,等边△ 中, 于 , ,点 、 分别为 、 上的两个定点且 ,在 上有一动点 使 最短,则 的最小值为 .
15. 如图,等边△ 中, 于 , ,点 、 分别为 、 上的两个定点且 ,在 上有一动点 使 最短,则 的最小值为 . 16. 如图,A、B、C、D、E、F、G都在∠O的边上,OA=AB=BC=CD=DE=EF=FG,若∠EFG=30°,则∠O= .
16. 如图,A、B、C、D、E、F、G都在∠O的边上,OA=AB=BC=CD=DE=EF=FG,若∠EFG=30°,则∠O= .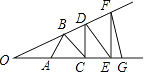
三、解答题
-
17. 如图,在△ABC中,∠BAC=90°,AD⊥BC,BE平分∠ABC,G为EF的中点,求证:AG⊥EF
 18. 如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G)
18. 如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD=CE.求证:△ABC是等腰三角形.(过D作DG∥AC交BC于G) 19. 如图,在△ABC中,AB=AC,点P 是BC边上的一点,PD⊥AB 于D ,PE⊥AC于E,CM⊥AB 于M,试探究线段PD、PE、CM的数量关系,并说明理由。
19. 如图,在△ABC中,AB=AC,点P 是BC边上的一点,PD⊥AB 于D ,PE⊥AC于E,CM⊥AB 于M,试探究线段PD、PE、CM的数量关系,并说明理由。 20. 已知:如图,BD、CE是△ABC的高,F是BC的中点,G是ED的中点,求证:FG⊥DE.
20. 已知:如图,BD、CE是△ABC的高,F是BC的中点,G是ED的中点,求证:FG⊥DE.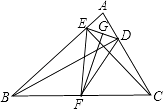 21. 如图
21. 如图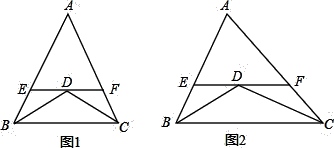
 (1)、如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有个等腰三角形;EF与BE、CF之间的数量关系是 , △AEF的周长是;(2)、如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有多少个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;(3)、已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.22. 如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,
(1)、如图1,已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,分别交AB、AC于E、F两点,则图中共有个等腰三角形;EF与BE、CF之间的数量关系是 , △AEF的周长是;(2)、如图2,若将(1)中“△ABC中,AB=AC=10”该为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有多少个等腰三角形;EF与BE、CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长;(3)、已知:如图3,D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE∥BC,分别交AB、AC于E、F两点,则EF与BE、CF之间又有何数量关系呢?直接写出结论不证明.22. 如图1,△ABC中,CD⊥AB于D,且BD:AD:CD=2:3:4,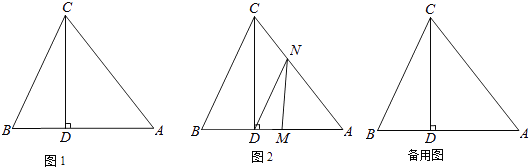 (1)、试说明△ABC是等腰三角形;(2)、已知S△ABC=40cm2 , 如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),
(1)、试说明△ABC是等腰三角形;(2)、已知S△ABC=40cm2 , 如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.