初中数学苏科版八年级上册2.4.2 角的轴对称性 同步练习
试卷更新日期:2020-09-17 类型:同步测试
一、单选题
-
1. 在△ABC 内一点 P 到三边的距离相等,则点 P 一定是△ABC 的( )A、三边垂直平分线的交点 B、三条内角平分线的交点 C、三条高的交点 D、三条中线的交点2. 如图,在四边形ABDC中,∠B=∠D=90°,∠BAC与∠ACD的平分线交于点O,且点O在线段BD上,BD=4,则点O到边AC的距离是( )
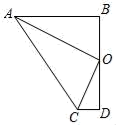 A、1 B、1.5 C、2 D、33. 如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则ΔDBE的周长是( )
A、1 B、1.5 C、2 D、33. 如图,在ΔABC中,∠C=90°,AC=BC,AD平分∠CAB交BC于D,DE⊥AB于E,若AB=6cm,则ΔDBE的周长是( )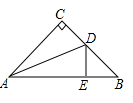 A、6cm B、7cm C、8cm D、9 cm4. 已知∠AOB=80°,∠BOC=30°,OM平分∠ AOB, ON平分∠AOC则∠MON的度数为( )A、15° B、15°或55° C、30°或110° D、30°或55°5. 如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )
A、6cm B、7cm C、8cm D、9 cm4. 已知∠AOB=80°,∠BOC=30°,OM平分∠ AOB, ON平分∠AOC则∠MON的度数为( )A、15° B、15°或55° C、30°或110° D、30°或55°5. 如图, 中, , 平分 , 于点 , 于点 , ,则 的长为( )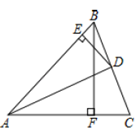 A、3 B、4 C、5 D、66. 如图, 是 的角平分线, , , , 分别是垂足,若 , ,则 的长为( )
A、3 B、4 C、5 D、66. 如图, 是 的角平分线, , , , 分别是垂足,若 , ,则 的长为( )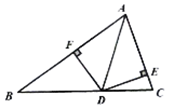 A、3 B、6 C、9 D、127. 如图,AD是∆ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7 ,DE=2,AB=4,则AC的长是( )
A、3 B、6 C、9 D、127. 如图,AD是∆ABC中∠BAC的平分线,DE⊥AB于点E,S△ABC=7 ,DE=2,AB=4,则AC的长是( )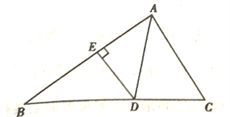 A、3 B、4 C、5 D、68. 如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )
A、3 B、4 C、5 D、68. 如图,BP平分∠ABC,D为BP上一点,E,F分别在BA,BC上,且满足DE=DF,若∠BED=140°,则∠BFD的度数是( )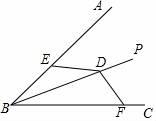 A、40° B、50° C、60° D、70°9. 点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )A、PQ>5 B、PQ<5 C、PQ≥5 D、PQ≤510. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P , BE=BC , PB与CE交于点H , PG∥AD交BC于F , 交AB于G , 连接CP . 下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF . 其中,正确有( )
A、40° B、50° C、60° D、70°9. 点P在∠AOB的平分线上,点P到OA边的距离等于5,点Q是OB边上的任意一点,则下列选项正确的是( )A、PQ>5 B、PQ<5 C、PQ≥5 D、PQ≤510. 如图所示,在△ABC中,内角∠BAC与外角∠CBE的平分线相交于点P , BE=BC , PB与CE交于点H , PG∥AD交BC于F , 交AB于G , 连接CP . 下列结论:①∠ACB=2∠APB;②S△PAC:S△PAB=AC:AB;③BP垂直平分CE;④∠PCF=∠CPF . 其中,正确有( )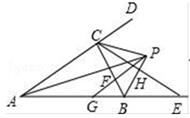 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 如图,已知 的周长是18,OB,OC分别平分 和 , 于D,且 ,则 的面积是.
 12. 如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D.已知BD:CD=3:2,点D到AB的距离是6,则BC的长是 .
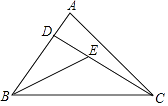
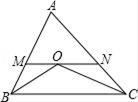
12. 如图,△ABC中,∠C=90°,AD平分∠BAC交BC于点D.已知BD:CD=3:2,点D到AB的距离是6,则BC的长是 .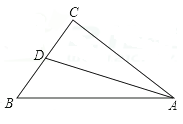 13. 如图,在△ABC中,∠B与∠C的平分线交于点O , 过点O作MN∥BC , 分别交A
13. 如图,在△ABC中,∠B与∠C的平分线交于点O , 过点O作MN∥BC , 分别交AB、AC于点M , N . 若AB=8,AC=10,则△AMN的周长是 .
 14. 如图,AB∥CD,∠BAC与∠ACD的平分线交于点P,过P作PE⊥AB于E,交CD于F,EF=10,则点P到AC的距离为 .
14. 如图,AB∥CD,∠BAC与∠ACD的平分线交于点P,过P作PE⊥AB于E,交CD于F,EF=10,则点P到AC的距离为 .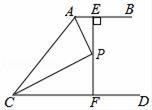 15. 如图,在△ABC中,∠ABC与∠ACB的外角平分线交于点P,PM⊥AC于点M.若PM=6cm,则点P到AB的距离为cm.
15. 如图,在△ABC中,∠ABC与∠ACB的外角平分线交于点P,PM⊥AC于点M.若PM=6cm,则点P到AB的距离为cm.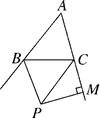 16. 如图,∠AOB=30°,P是∠AOB的角平分线上的一点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN= .
16. 如图,∠AOB=30°,P是∠AOB的角平分线上的一点,PM⊥OB于点M,PN∥OB交OA于点N,若PM=1,则PN= .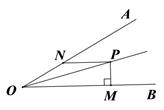 17. 如图,钝角三角形ABC的面积为30,最长边AB=20,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值是 .
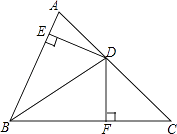
17. 如图,钝角三角形ABC的面积为30,最长边AB=20,BD平分∠ABC,点M、N分别是BD、BC上的动点,则CM+MN的最小值是 .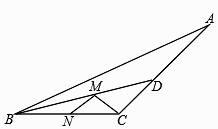 18. 如图,R△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为。
18. 如图,R△ABC中,∠C=90°,∠BAC的角平分线AE与AC的中线BD交于点F,P为CE中点,连结PF,若CP=2,S△BFP=15,则AB的长度为。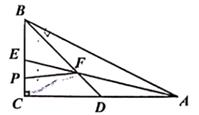
三、解答题
-
19. 尺规作图:如图,在直线MN上求作一点P,使点P到 ∠AOB两边的距离相等(不要求写出作法,但要保留作图痕迹,写出结论)
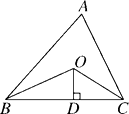
 20. 如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=20,过O作OD⊥BC于D点,且OD=3,求△ABC的面积.
20. 如图,在△ABC中,点O是∠ABC、∠ACB平分线的交点,AB+BC+AC=20,过O作OD⊥BC于D点,且OD=3,求△ABC的面积.