山东省潍坊市临朐县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 下列设计的图案中,既是轴对称图象又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各式中,正确的是( )A、 B、 C、 D、3. 已知函数 是关于x的一次函数,则m的值是( )A、 B、 C、 D、4. 实数a,b在数轴上的位置如图所示,则下列不等关系正确的是( )
2. 下列各式中,正确的是( )A、 B、 C、 D、3. 已知函数 是关于x的一次函数,则m的值是( )A、 B、 C、 D、4. 实数a,b在数轴上的位置如图所示,则下列不等关系正确的是( ) A、 B、 C、 D、5. 已知a,b,c是三角形三边,满足 ,则三角形的形状是( )A、腰和底不相等的等腰三角形 B、等边三角形 C、钝角三角形 D、直角三角形6. 已知变量y与x之间的关系满足如图,那么能反映y与x 之间函数关系的解析式是( )
A、 B、 C、 D、5. 已知a,b,c是三角形三边,满足 ,则三角形的形状是( )A、腰和底不相等的等腰三角形 B、等边三角形 C、钝角三角形 D、直角三角形6. 已知变量y与x之间的关系满足如图,那么能反映y与x 之间函数关系的解析式是( ) A、 B、 C、 D、7. 如图,将 绕点O逆时针方向旋转45度后得到 ,若 ,则 的度数是( )
A、 B、 C、 D、7. 如图,将 绕点O逆时针方向旋转45度后得到 ,若 ,则 的度数是( ) A、 B、 C、 D、8. 若点P(a+1,a﹣2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是( )A、
A、 B、 C、 D、8. 若点P(a+1,a﹣2)关于原点对称的点位于第二象限,则a的取值范围表示正确的是( )A、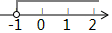 B、
B、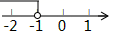 C、
C、 D、
D、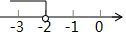 9. 如图,一次函数 与 的图像相交于点P(m,4),则使得 的x的取值范围是( )
9. 如图,一次函数 与 的图像相交于点P(m,4),则使得 的x的取值范围是( ) A、 B、 C、 D、10. 如图,在平面直角坐标系中,将 绕着旋转中心顺时针旋转 ,得到 ,则旋转中心的坐标为( )
A、 B、 C、 D、10. 如图,在平面直角坐标系中,将 绕着旋转中心顺时针旋转 ,得到 ,则旋转中心的坐标为( ) A、 B、 C、 D、11. 关于x的不等式组 有且仅有三个整数解,则所有正确的整数k的和是( )A、 B、 C、 D、12. 如图,点 ,点 向上平移1个单位,再向右平移2个单位.得到 ;点 向上平移2个单位,再向右平移4个单位,得到点 ;点 向上平移4个单位,再向右平移8个单位,得到点 ……按照这个规律得到 ,则点 的横坐标为( )
A、 B、 C、 D、11. 关于x的不等式组 有且仅有三个整数解,则所有正确的整数k的和是( )A、 B、 C、 D、12. 如图,点 ,点 向上平移1个单位,再向右平移2个单位.得到 ;点 向上平移2个单位,再向右平移4个单位,得到点 ;点 向上平移4个单位,再向右平移8个单位,得到点 ……按照这个规律得到 ,则点 的横坐标为( )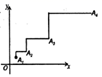 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 下列二次根式,不能与 合并的是(填写序号)
① ;② ;③ ;④
14. 若一次函数 的图像不经过第三象限,则k的取值范围是 .15. 如图, 沿BC方向平移4cm,得到 ,如果四边形ABFD的周长是32cm,则 的周长是cm. 16. 如图是一个正方形的表面展开图,已知正方体的每个面都有一个实数,且相对面上的两个数互为倒数,则xyz的平方根是 .
16. 如图是一个正方形的表面展开图,已知正方体的每个面都有一个实数,且相对面上的两个数互为倒数,则xyz的平方根是 . 17. 在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对了得10分,答错了或不答扣5分,小明要想在竞赛中得分不少于100分,则他至少要答对道题.18. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.
17. 在一次绿色环保知识竞赛中,共有20道题,对于每一道题,答对了得10分,答错了或不答扣5分,小明要想在竞赛中得分不少于100分,则他至少要答对道题.18. 某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后卸完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示.
现有以下4个结论:
①快递车从甲地到乙地的速度为100千米/小时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3.75,75);
④快递车从乙地返回时的速度为90千米/小时
以上结论正确的是 .
三、解答题
-
19.(1)、解不等式 ,并把它的解集在数轴上表示出来;(2)、解不等式组:20. 计算:(1)、(2)、21. 如图, 三个顶点的坐标分别是 ,
 (1)、请画出 向左平移6个单位后得到的 ,并写出 的坐标;(2)、请画出 关于原点对称的 ,并写出点 的坐标;(3)、在x轴上求一点P使 周长最小(保留作图痕迹,不写作法)22. 一次函数的图象过点(-2,3),(1,3)两点(1)、求出一次函数解析式;(2)、当函数值y满足 时,求自变量x的取值范围;(3)、求该图像与坐标轴围成的三角形的面积.23. 如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 .
(1)、请画出 向左平移6个单位后得到的 ,并写出 的坐标;(2)、请画出 关于原点对称的 ,并写出点 的坐标;(3)、在x轴上求一点P使 周长最小(保留作图痕迹,不写作法)22. 一次函数的图象过点(-2,3),(1,3)两点(1)、求出一次函数解析式;(2)、当函数值y满足 时,求自变量x的取值范围;(3)、求该图像与坐标轴围成的三角形的面积.23. 如图,一架 长的梯子 斜靠在一竖直墙 上,这时 为 . (1)、求 的长度;(2)、如果梯子底端 沿地面向外移动 到达点 ,那么梯子顶端 下移多少 ?24. 为了加强学生球类运动的训练,某学校计划购买篮球和排球共30个,已知每个篮球80元,每个排球60元,设购买排球x个,购买排球和篮球的总费用为y元(1)、求y与x的函数表达式;(2)、如果要求篮球的个数不少于排球个数的5倍,应如何购买才能使总费用最少?最少费用是多少?25. 如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG.
(1)、求 的长度;(2)、如果梯子底端 沿地面向外移动 到达点 ,那么梯子顶端 下移多少 ?24. 为了加强学生球类运动的训练,某学校计划购买篮球和排球共30个,已知每个篮球80元,每个排球60元,设购买排球x个,购买排球和篮球的总费用为y元(1)、求y与x的函数表达式;(2)、如果要求篮球的个数不少于排球个数的5倍,应如何购买才能使总费用最少?最少费用是多少?25. 如图①,已知△ABC是等腰直角三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A,C分别在DG和DE上,连接AE,BG. (1)、请写出线段BG和AE的位置关系及数量关系;(2)、如图②,将正方形DEFG绕点D逆时针方向旋转一定的角度 ,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)、若BC=DE=4,正方形DEFG绕点D逆时针方向旋转角度 的过程中,当AE为最大值时,请直接写出AF的值.
(1)、请写出线段BG和AE的位置关系及数量关系;(2)、如图②,将正方形DEFG绕点D逆时针方向旋转一定的角度 ,(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由;(3)、若BC=DE=4,正方形DEFG绕点D逆时针方向旋转角度 的过程中,当AE为最大值时,请直接写出AF的值.