山东省日照市莒县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2020-09-17 类型:期末考试
一、单选题
-
1. 一元二次方程 的一次项系数为( )A、 B、 C、 D、2. 在下列图形性质中,平行四边形不一定具备的是( )A、两组对边分别相等 B、对角线互相平分 C、两组对边分别平行 D、对角线相等3. 已知一次函数y=kx-k,若y随x的增大而增大,则图象经过( )A、第一、二、三象限 B、第一、三、四象限 C、第一、二、四象限 D、第二、三、四象限4. 为了解某种电动汽车一次充电后行驶的里程数,抽检了 辆车,对一次充电后行驶的里程数进行了统计,结果如图所示,则在这组数据中,众数和中位数分别是( )
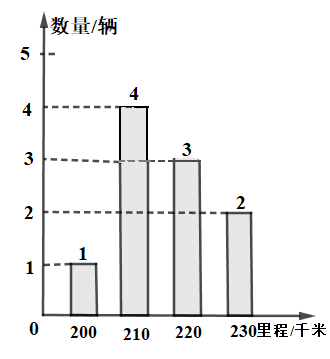 A、 B、 C、 D、5. 方程 的解是( )A、 B、 C、 D、6. 如图,周长为 的菱形 中,点 分别在边 上, 为 上一动点,则线段 长度的最小值为( )
A、 B、 C、 D、5. 方程 的解是( )A、 B、 C、 D、6. 如图,周长为 的菱形 中,点 分别在边 上, 为 上一动点,则线段 长度的最小值为( ) A、 B、 C、 D、7. 一个装有进水管和出水管的空容器,从某时刻开始 内只进水不出水,容器内存水 ,在随后的 内既进水又出水,容器内存水 ,接着关闭进水管直到容器内的水放完.若每分钟进水和出水量是两个常数,容器内的水量 (单位: )与时间 (单位: )之间的函数关系的图象大致的是( )A、
A、 B、 C、 D、7. 一个装有进水管和出水管的空容器,从某时刻开始 内只进水不出水,容器内存水 ,在随后的 内既进水又出水,容器内存水 ,接着关闭进水管直到容器内的水放完.若每分钟进水和出水量是两个常数,容器内的水量 (单位: )与时间 (单位: )之间的函数关系的图象大致的是( )A、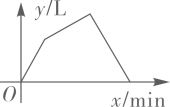 B、
B、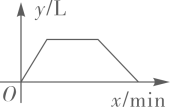 C、
C、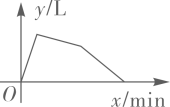 D、
D、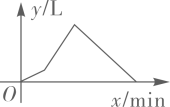 8. 一次函数 的图象如图所示,当 时,x的取值范围是( )
8. 一次函数 的图象如图所示,当 时,x的取值范围是( )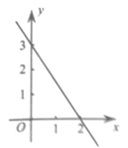 A、 B、 C、 D、9. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )
A、 B、 C、 D、9. 如图,在直角坐标系中,已知菱形OABC的顶点A(1,2),B(3,3).作菱形OABC关于y轴的对称图形OA′B′C′,再作图形OA′B′C′关于点O的中心对称图形OA″B″C″,则点C的对应点C″的坐标是( )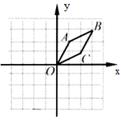 A、(2,-1) B、(1,-2) C、(-2,1) D、(-2,-1)10. 如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )
A、(2,-1) B、(1,-2) C、(-2,1) D、(-2,-1)10. 如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( )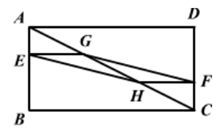 A、1 B、 C、2 D、411. 在同一坐标系中,二次函数 与一次函数 的图象可能是( )A、
A、1 B、 C、2 D、411. 在同一坐标系中,二次函数 与一次函数 的图象可能是( )A、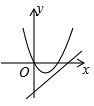 B、
B、 C、
C、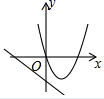 D、
D、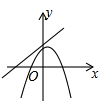 12. 二次函数 ( 是常数, )的自变量 与函数值 的部分对应值如下表:
12. 二次函数 ( 是常数, )的自变量 与函数值 的部分对应值如下表:…
0
1
2
…
…
…
且当 时,与其对应的函数值 .有下列结论:① ;② 和3是关于 的方程 的两个根;③ .其中,符合题意结论的个数是( )
A、0 B、1 C、2 D、3二、填空题
-
13. 一组数据1,3,8,9,6,4的中位数是 .14. 如图,若被击打的小球飞行高度 (单位: )与飞行时间 (单位: )直接具有的关系为 ,则小球从飞出到落地所用的时间为s.
 15. 在平面直角坐标系 中,将函数 图象向右平移 个单位长度,则平移后的图象与 轴、 轴分别交于 两点,则 的面积为 .16. 如图,在正方形 中, 与 交于点 是 的中点,点 在 边上,且 为对角线 上一点, 则 的最大值为 .
15. 在平面直角坐标系 中,将函数 图象向右平移 个单位长度,则平移后的图象与 轴、 轴分别交于 两点,则 的面积为 .16. 如图,在正方形 中, 与 交于点 是 的中点,点 在 边上,且 为对角线 上一点, 则 的最大值为 .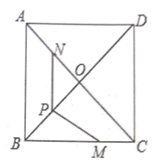
三、解答题
-
17.(1)、解方程: ;(2)、某校为解决大班额问题,拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为 分、 分、 分,综合成绩笔试占 ,试讲占 ,面试占 ,求该名教师的综合成绩?18. 某球队从队员中选拔选手参加 分球大赛,对报名的两名选手进行 分球投篮测试,测试共五组,每组投 次,进球的个数统计结果如表,经过计算,甲进球的平均数为 , 方差为
队员
进球数(个/组)
一
二
三
四
五
甲
10
6
10
6
8
乙
7
9
7
8
9
(1)、求乙进球的平均数 和方差 :(2)、现从甲、乙两名队员中选出一人去参加 分球投篮大赛,你认为应该选哪名队员去?为什么?19. “绿水青山就是金山银山”,为加快城乡绿化建设,某市2018年绿化面积约 万平方米,预计 年绿化面积约为 万平方米.假设每年绿化面积的平均增长率相同.(1)、求每年绿化面积的平均增长率;(2)、已知每平方米绿化面积的投资成本为 元,若 年的绿化面积继续保持相同的增长率,那么 年的绿化投资成本需要多少元?20. 如图, 是正方形 的对角线 上的两点,且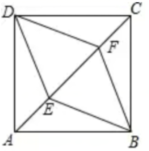 (1)、求证:四边形 是菱形:(2)、若正方形边长为 求菱形 的面积
(1)、求证:四边形 是菱形:(2)、若正方形边长为 求菱形 的面积